ZAD1.

Dwa jednakowe czwórniki połączone kaskadowo jak na rys. Obciążone układu czwórników stanoski Ro=100. Wartość skuteczna prądu sinusiodalnego zamiennego płynącego przez ten odbiornik wynosi 1A. Macierz każdego czwórnika wynosi A.

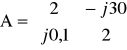
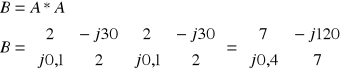
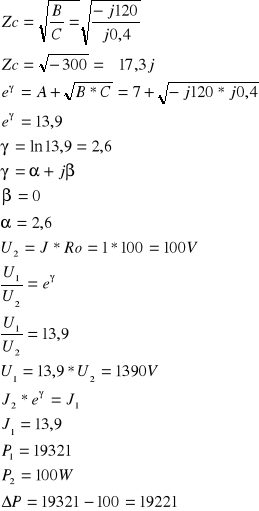
ZAD2.

Czwórnik jest zasilana napięciem sinusiodalnym. Wyznaczyć: macierz łańcuchową czwórnika, impedancje Zc w przypadku równości Xc1=Xc2, oraz X_L=Xc.

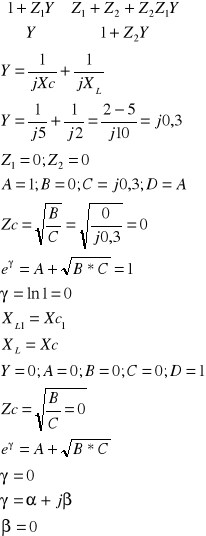
ZAD3.

wyznaczyć jego elementy i narysować schemat połączeń, pulsacja ω=100; obliczyć współczynnik α, β oraz Z_C dla czwórnika zastępczego.

U₁=U₂*A+J₂*B

J₂=U₂*C+J₂*D

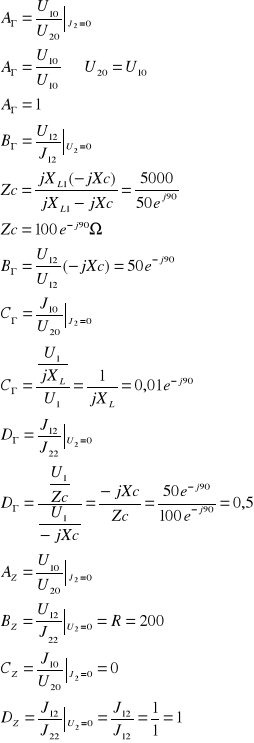
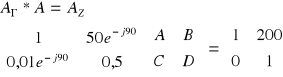
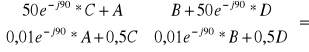
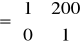
A-j50C=1A C=j0,02A A-j50*j0,02A=1

A+A=1 A=0,5 C=j0,02*0,5

C=j0,01 0,5D=1+j0,01B D=2+j0,02B

B=200+j50D=200+j50(2+j0,02B)=200+j100+j²B

B=200+j100-B 2B=200+j100 B=100+j50

D=2+j0,02(100+j50)=2+j3+j²1=2+j3-1

D=1+j2

A=1+Z₁*Y B=Z₁+Z₂+Z₁*Z₂*Y C=Y

D=1+Z₂*Y Y=j0,01s ω_c=0,01

C=0,01/100=100μF A=1+Z₁*Y (0,5-1)/Y=Z₁

-1/2Y=Z₁ Z₁=j50 D=1+Z₂*Y

(1+j2-1)/Y=Z₂ Z₂=j₂/j0,01=2*100 Z₂=200Ω

Ponieważ czwórnik jest symetryczny (A=D) to impedancja falowa będzie równa:

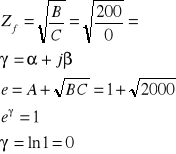
ZAD.4

Dany jest czwórnik jak na rys.. Dobrać tak rezystancję R aby impedancja falowa Zf czwórnika miała zadana wartość. Obliczyć współczynnik przenoszenia falowego.

Równania łańcuchowe:

U1=AU2+BI2

I1=CU2+DI2

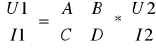
A1

Stan jałowy - przy I2=0 , U1=U2

A1=U1/U2=U1/U1=1

C1=I1/U2=0/U1=0

Stan zwarcia - przy U2=0 , I1=I2

B1=U1/I2=U1/I1=U1/(U1/0,5R)=0,5R

D1=I1/I2=I1/I1=1

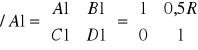
A2

Stan jałowy - przy I2=0 , U1=U2

A2=U1/U2=U1/U1=1

C2=I1/U2=(U1/R)/U1=1/R

Stan zwarcia - przy U2=0 , I1=I2

B1=U1/I2=0

D1=I1/I2=I1/I1=1

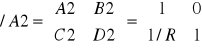
/A1=/A2

/A=/A1*/A2*/A3

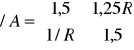
A=D - więc czwórnik jest symetryczny

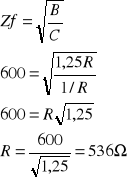
γ=α+jβ α - współ. tłumienia

β - współ. przesunięcia fazowego

Dla czwórnika czysto rezystancyjnego β=0

e^α=A+√BC e^α=1,5+√1,25R*1/R e^α=1,5+√1,25 e^α=2,61 α=ln2,61 α=0,96 γ=α γ=0,96

Równania łańcuchowe czwórników

I1 = I'2 I2 = I'2

U1=AU2+BI2

I1=CU2+DI2

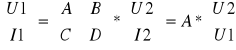
A - macierz łańcuchowa czwórnika

Warunek odwracalności czwórnika

AD - BC = 1

Jeżeli A=D, to czwórnik jest symetryczny, jeżeli A≠D to czwórnik jest niesymetryczny.

Jeżeli znane są napięcia U1 i U2 to prądy wyznacza się na podstawie równania admitancyjnego czwórnika

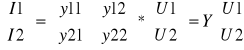
Y - macierz admitancyjna czwórnika

Jeżeli znane są prądy to nap. na wej. i wyj. wyznacza się na podstawie równań impedancyjnych

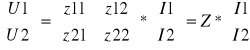
Z - macierz impedancyjna czwórnika

Impedancja falowa na wej.

Impedancja falowa na wyj.

Gdy A=D to Zf obu stron są równe

Parametry łańcuchowe czwórnika:

A=U₁₀ / U₂₀ przy I₂=0 - stan jałowy czwórnika

B=U_1Z / I_2Z przy U₂=0 - stan zwarcia

C=I₁₀ / U₂₀ przy I₂=0 - stan jałowy

D=I_1Z / I_2Z przy U₂=0 -stan zwarcia

Impedancja na wej. w stanie jałowym:

Z₁₀=U₁₀ / I₁₀ = A/C

Impedancja na wyj. w stanie zwarcia:

Z_1Z=U_2Z / I_2Z =B/D

Współczynnik przesunięcia fazowego

γ=α+jβ α - współ. tłumienia

β - współ. przesunięcia fazowego

Dla czwórników czysto rezystancyjnych β=0

e^α = A+√BC

Połączenie łańcuchowe (kaskadowe) czwórników

I₁=I'₁ , I'₂=I”₁ , I₂=I”₂ , U1=U'₁ , U'₂=U”₁ , U₂=U”₂

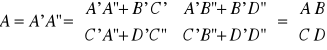
Połączenie szeregowe czwórników

I₁=I'₁=I”₁ , I₁=I'₂=I”₂ , U₁=U'₁+U”₁ , U₁=U'₂=U”₂

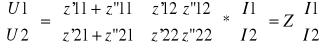
Z=Z'+Z”

Połączenie równoległe czwórników

U₁=U'₁=U”₁ , U₂=U'₂=U”₂ , I₁=I'₁+I'₁ , I₂=I'₂=I”₂

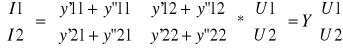
Y=Y'+Y"

ZAD.5

Łańcuch 4 czwórników obciążony jest impedancją falową Zf. Współ. przenoszenia jednego ogniwa wynosi γ. obliczyć wskazania mierników oraz wartość chwilową prądu na wyj. ostatniego ogniwa.

U19t)=80√2 sin ωt Zf=10e ^j30 Ω γ=ln2-jπ/6

I1=U1/Zf=80e ^j0/10e ^j30=8e^-j30 I1/I2=e^2γ

I2=I1*e^-2γ =8e^-j30 * e^{2 (ln2-jπ/6)} = 8e^-j30 * e ^-2ln2= 2e^j30

A2 → 2A

I2=U2/Zf U2=I2*Zf=20e ^j60

V2 → 20V

S=UI^∗ P2=Re(S2)=Re(2e^-j30 * 20e ^{j 60}) P2=Re(34,6+j20)

W2 → 34,6W

I2/I4=e^2γ I4=I2* e^-2γ=0,5e ^{j 90}

A4 → 0,54A

U4=I4*Zf=5e ^{j 120}

V4 → 5V

P4=S4=Re(S4)=Re(U4*I4^*)=Re(2,16+j1,25)

W4 → 2,16W

---