KF PŚk
O5		Wyznaczanie stałej siatki dyfrakcyjnej i długości fal świetlnych

WSTĘP

Siatkę dyfrakcyjną stanowi szereg szczelin umieszczonych w równych od siebie w nieprzezroczystym ekranie. W praktyce siatkę dyfrakcyjną otrzymuje się najczęściej przez rysowanie płasko-równoległej płytki szklanej za pomocą diamentu szeregiem równoległych kresek. Nieprzezroczyste rysy odgrywają rolę zasłon, a przestrzenie między rysami - to szczeliny. Jeśli taką siatkę dyfrakcyjną prostopadle do jej powierzchni pada wiązka promieni równoległych, to - zgodnie z zasadą Huygensa - każda szczelina staje się źródłem drgań i wysyła promienie we wszystkich kierunkach, a więc nie tylko w kierunku promieni padających. Zjawisko to nazywa się dyfrakcją, czyli interferować ze sobą, gdyż są promieniami spójnymi: znaczy to, że różnice faz między nimi zależą tylko do różnic dróg geometrycznych nie zależą zaś od czasu. Biorąc pod uwagę wiązki promieni ugiętych zauważyć można, że w pewnych kierunkach promienie te będą się wzmacniały, w innych zaś - wygaszały ( częściowo lub zupełnie ) promienie będą się wzmacniać, jeżeli różnice dwóch sąsiednich promieni będą równe całkowitej wielokrotności długości fali światła padającego.

Warunek wzmocnienia promieni ugiętych na siatce dyfrakcyjnej ma postać

n λ = d sin ϕ

gdzie:

d - oznacza odległość między szczelinami `stała siatki dyfrakcyjnej `

n - rząd widma

λ - długość fali

POMIARY

Pomiar	L (mm)	x(mm)
1	455	60
				125
				195
		2	388	50
				105
				165

OBLICZENIE STAŁEJ SIATKI DYFRAKCYJNEJ

gdzie,

d - odległość miedzy sąsiednimi szczelinami

n - rząd widma

x - położenie rzędu widma

L - odległość siatki dyfrakcyjnej od ekranu

λ - długość fali = 0,6328 μm

=

=

=

=

=

=

ZESTAWIENIE WYNIKÓW W TABELI

Pomiar	L(mm)	X(mm)	rząd	d(μm)
1	455	60	1	4,80
				125	2	4,78
				195	3	4,81
		2	388	50	1	4,95
				105	2	4,84
				165	3	4,85

Jako wartość stałej siatki dyfrakcyjnej przyjmuję średnią ze wszystkich pomiarów:

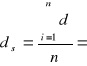
4,84

Obliczanie błędów:

l =
1mm

x =
1mm

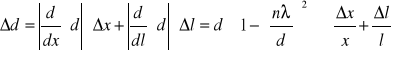
d₁=0,007

d₂=0,004

d₃=0,002

d₄=0,009

d₅=0,004

d₆=0,003

d_śr=0,0048

Zestawienie wszystkich wyników w tabeli

Pomiar	L(mm)	X(mm)	rząd	d(μm)	Δd	(μm)
1	455	60	1	4,80	0,007	4,80 0,007
				125	2	4,78	0,004	4,78 0,004
				195	3	4,81	0,002	4,81 0,002
		2	388	50	1	4,95	0,009	4,95 0,009
				105	2	4,84	0,004	4,84 0,004
				165	3	4,85	0,003	4,85 0,003

Wyniki otrzymane przez nas po wykonaniu doświadczenia są obarczone błędem. Można tu zaliczyć błąd niedokładności spisywanych wartości obliczanych wcześniej na kalkulatorze a także błędem paralaksy gdyż wykonywane ćwiczenie miało swe podłoże w odczytywaniu wyników z podziałki zrobionej z papieru milimetrowego, a lekkie kłopoty ze wzrokiem uczestników oraz ciemność panująca w pracowni fizycznej uniemożliwiały dokładny odczyt wartości padającej plamki na ekran.

Wnioski:

W większości doświadczeniach optycznych mamy do czynienia z badaniem własności fizycznych, które są już od wieków ustalone. Natomiast nasze doświadczenia maja na celu sprawdzenie ich oraz rozwijanie myślenia abstrakcyjnego.

Na podstawie dokonanych pomiarów i obliczeń możemy stwierdzić, iż przy poszczególnych rzędach odległość między szczelinami zmniejsza się.

---