UWAGA!!!
Pytania zostały opracowane na podstawie notatek własnych, książki Śledzia, jego kserówek, trochę znalazłem w internecie, część skopiowałem od osoby której się rok temu chciało. W związku z tym nie biorę odpowiedzialności za szkody wynikłe z ewentualnych nieprawidłowości w informacjach zawartych w poniższym opracowaniu. Kolejną przykrą sprawą jest fakt, że wiele zagadnień które otrzymaliśmy nie było poruszane na wykładach. Z tego min. powodu kilka pytań nie ma odpowiedzi, a kilka ma niezbyt konkretne i niezbyt wyczerpujące. Z drugiej strony, niektóre zagadnienia są opracowane aż nazbyt obszernie. Nie miałem po prostu czasu na dokładną selekcje i wklejałem fragmenty notatek jak leciało. Kolejną przykrą sprawą (dla tych co piszą zerówkę) jest fakt że na stan dzisiejszy (2 VI 2006) jeszcze jeden wykład przed nami (i to podobno najtrudniejszy ze wszystkich). Zagadnienia które będą na nim poruszane to w sumie 10 pytań. Pytania te, puki co nie znalazły się w poniższym opracowaniu.
Jeśli zauważył(eś/aś) jakiś błąd (nie składniowy, czy stylistyczny), lub znasz odpowiedz na któreś z nieopracowanych zagadnień to pisz:
w tytule maila „satka”, proszę podawać dokładnie którego pytania, z którego działu problem dotyczy. Jeśli otrzymam coś sensownego to postaram się wrzucić erratę.
Zagadnienia wstępne
1. Czym zajmuje się geodezja satelitarna?
Wyznaczenie położenia (pozycji) punktów geodezyjnych (zastabilizowanych) i obiektów ruchomych. Punkty geodezyjne nie są tak naprawdę stałe, bo też się poruszają. Geodezja i nawigacja wyznaczają położenie z tym że geodezja punktów zastabilizowanych (względnie nieruchomych) a nawigacja - obiektów ruchomych. Zastosowanie obserwacji SSZ pozwala na:
Tworzenie precyzyjnych:
globalnych
regionalnych
lokalnych
przestrzennych sieci geodezyjnych
Tworzenie systemów nawigacyjnych (stacji referencyjnych)
Wyznaczenie modeli pola grawitacyjnego Ziemi i funkcji tego pola
Spłaszczenie Ziemi
Kształt elipsoidy
Odchylenie linii pionu
Anomalie grawimetryczne
Pomiar, monitorowanie i modelowanie zjawisk geodynamicznych:
Ruch bieguna
Stabilność ruch obrotowego Ziemi
Pływy
Ruch skorupy Ziemskiej
itp.
SSZ mogą mieć orbity o różnym nachyleniu względem równika,
SSZ mogą poruszać się w żądanej (najkorzystniejszej) odległości od Ziemi (np. do wyznaczania pola grawitacyjnego Ziemi wykorzystuje się ciężkie i niskie satelity),
SSZ mogą być aktywne (tzn. mogą mieć zainstalowaną na pokładzie aktywnie pracującą aparaturę: nadajnik, radary itd.).
geometryczne, odległość 384 tys. km daje niekorzystny kształt figur geometrycznych (dla wcięć),
dynamiczne, ze względu na zbyt dużą odległość jest mało czuły na wpływy nierównomierności pola grawitacyjnego.
ruch odbywa się ściśle według praw Keplera
ruch odbywa się w centralnym polu grawitacyjnym, wyłącznie pod wpływem sił grawitacyjnych
jest to więc ruch punktu materialnego wokół ciała (punktu) centralnego
upraszczając: ruch punktu wokół punktu
związane jest z tym zadanie dwóch ciał (Ziemia + Satelita), które ma jednoznaczne rozwiązanie matematyczne
elementy orbity keplerowskiej są stałe w czasie
Promień wodzący satelity zakreśla w równych interwałach czasu równe pola
Pole (S) zakreślone promieniem wodzącym satelity jest proporcjonalne do czasu
Prędkość polowa
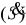
satelity jest stała (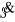
- zmiana pola w czasie)orbity kołowej
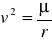
(a = r)orbity eliptycznej

(a>0)orbity parabolicznej
(a = h)orbity hiperbolicznej

(a<0)składowe wektorowej stałej pola
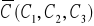
składowe wektora Laplace'a
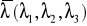
stała energii h
Niecentralność pola grawitacyjnego. Rzeczywiste pole grawitacyjne nie jest centralne. Spowodowane jest to:
Niecentralnością pola Ziemi - powodują je: spłaszczenie Ziemi, niesymetria mas Ziemi względem równika, eliptyczność równika, anomalie siły ciężkości (różna gęstość mas ziemi), siły pływowe itd.
Wpływami grawitacyjnymi innych ciał niebieskich: Księżyca, Słońca, planet (bliższych).
Siły elektromagnetyczne - wynikają one na skutek poruszania się metalowych części satelity w polu magnetycznym wytworzonym przez ciało centralne tj. Ziemie.
Opór atmosfery (dla bliższych satelitów)
Ciśnienie światła słonecznego
Promieniowanie odbite od Ziemi (albedo)
Pył kosmiczny
Efekty relatywistyczne
itd.
perturbacje krótkookresowe
perturbacje dobowe
perturbacje długookresowe
Perturbacja węzła wstępującego (obrót linii węzłów) - uwidacznia się ona w precesji płaszczyzny orbity, czyli obrocie płaszczyzny orbity względem osi Ziemi w kierunku przeciwnym do ruchu SSZ (dla i < 90°); nachylenie orbity do równika i pozostaje przy tym nie zmienione. Wynikiem tego zjawiska jest ustawiczne przesuwanie się po równiku węzła wstępującego orbity w kierunku przeciwnym do ruchu satelity. Ponieważ taki sam ruch opisuje również węzeł zstępujący orbity można powiedzieć, że omawiana perturbacja uwidacznia się jako ustawiczna zmiana linii węzłów. Prędkość tego ruchu dana jest wzorem:
Perturbacja wiekowa argumentu perigeum ω (obrót linii apsyd) - jest to obrót orbity SSZ w jej płaszczyźnie. Duża oś orbity obraca się w płaszczyźnie orbity, czego faktem jest ciągłe przemieszczanie się punktu perigeum (szerokość geograficzna punktu na Ziemi, nad którym przypada perigeum orbity, zmienia się). Ponieważ takich samych przemieszczeń doznaje i przeciwległy perigeum punkt orbity, czyli apogeum, przeto mówimy w tym wypadku o ruchu linii apsyd. Efekt ten nie występuje w przypadku orbit kołowych, dla których traci sens pojęcie linii apsyd. Prędkość obrotu linii apsyd jest dana wzorem:
Perturbacje wiekowe okresu obiegu satelity
wykonanie zdjęć
opracowanie fotochemiczne
identyfikacja gwiazd oporowych
pomiar współrzędnych płaskich x,y - śladu satelity gwiazd oporowych i znaczków czasowych na koordynometrze
transformacja współrzędnych płaskich na współrzędne ,δ
ocena dokładności
nie wymagają satelitów aktywnych
wyznaczone topocentryczne kierunki do satelity na wszystkich punktach obserwacyjnych odniesione są do wspólnego, jednolitego układu współrzędnych gwiazdowych α,δ i są obarczone tylko różnicową refrakcją satelitarną . Pomiary fotograficzne zapewniają więc właściwą orientację satelitarnych sieci geodezyjnych i mają duże znaczenie dla utworzenia jednolitego podstawowego układu odniesienia do badań geodynamicznych. Nie wystarczą jednak do określenia skali sieci ( tu wykorzystuje się inne metody , np. laserowe, elektroniczne odległości do satelity , dopplerowskie)
długości impulsu,
jakości impulsu,
dokładności zegarów i liczników.
bardzo dokładne wyznaczenie orbit satelitów (również dla specjalnych misji np. altimetria)
wyznaczenie ruchu bieguna i ruchu obrotowego Ziemi
wyznaczenie pola grawitacyjnego Ziemi
wyznaczenie pływów
wyznaczenie ruchów tektonicznych
wyznaczenie orbit
geodynamika
zespół satelitów,
sieć stacji śledzących,
stacje służby czasu,
centrum obliczeniowe,
stacje przekazujące dane do satelity
dwie stabilne częstotliwości,
sygnały czasu, wyznaczają granice całkowania o każdej parzystej minucie,
ekstrapolowane elementy orbity, możliwość wyznaczenia pozycji satelity.
zespołu satelitów
zespołu kontrolnego
użytkowników systemu
Pozycja satelitów (satellite Alamanach) Cykl przekazania do odbiornika informacji o położeniu 30 satelitów trwa około 12.5 minuty.
Satellite clock correction - poprawka zegara pokładowego
Signal health - zdrowie satelity - informuje jak w skali od 1 do 9 satelita się czuje, czy działa w sposób prawidłowy, na ile można mu ufać. Pogorszenie „zdrowia” satelity, może nastąpić np. podczas wczytywania danych z satelity, czy przesuwania go. Signal health mówi czy dobrze działa dany satelita, a nie cały system.
Telemetry word - sygnał ten pozwala rozpocząć pomiar odległości
Handover word - pozwala na zmianę wykorzystania kodu.
Satelity bloku I (SYN I - SYN 14) Satelity wprowadzone na orbitę w latach 1978 - 1985 z wyrzutni Vandenberg AFB Kalifornia za pomocą rakiet typu ATLAS. Satelity posiadają 3 zegary atomowe (cezowy i 2 rubinowe). Przewidywana żywotność wynosiła 5 lat, w rzeczywistości eksploatowano je znacznie dłużej.
Satelity bloku II (SYN 15 - SYN 21) Satelity te zostały zaprojektowane przez Rockwell International. Satelity wprowadzano na orbitę w okresie od listopada 1989 do października 1990. Konstrukcja umożliwiała działanie w ciągu 14 dni bez potrzeby kontaktu ze stacjami kontrolnymi.
Satelity bloku III (SYN 22 - SYN 40)
Satelity bloku II R (SYN 41 - SYN 62) Satelity zaprojektowane zostały przez Lockhead Martin.
Satelity Bloku II F (Follow-up Satelites) Są to satelity przyszłej generacji GPS. Przewidywane wprowadzenie na orbitę w 2005 roku. Czas żywotności wydłużony do 12.8 lat. Na satelitach tych zainstalowane zostały lustra laserowe.
Wyznaczany punkt leży na przecięciu trzech kul zatoczonych ze środków położonych w trzech znanych położeniach satelitów.
Geometryczna procedura „trysferacji”
Geodezyjna procedura liniowego przestrzennego wcięcia wstecz
dokładność metrowa
jeden pomiar kodowy odległości do 4 satelitów pozwala na wyznaczenie położenia punktu w czasie rzeczywistym
nie jest wymagana inicjalizacja odbiornika
metoda wygodna w zastosowaniach nawigacyjnych
satelita emituje kod, a odbiornik w tym samym momencie taki sam kod (replica code)
kod emitowany przez satelitę docierający do odbiornika jest przesunięty w czasie. Przesunięcie to jest miarą czasu przebiegu sygnału satelita - odbiornik (Δt) i jest proporcjonalne do odległości satelita - odbiornik (d)
w odbiorniku następuje przesunięcie kodów do uzyskania korelacji i pomiar czasu Δt
mierzona odległość satelita - odbiornik wyraża się zależnością:
dokładność „centymetrowa” i „milimetrowa”, a więc dokładniejsza od kodowej
wymagana inicjalizacja odbiornika (wyznaczenie pełnej liczby cykli N)
obecnie często stosowana metoda szybkiej inicjalizacji OTF („on - the - fly”) wymagająca łącznego wykorzystania pomiarów kodowych i fazowych
odbiornik mierzy fazę φ (część pełnego cyklu) przychodzącej fali (sygnału)
mierzoną odległość satelita - odbiornik wyraża się zależnością:
niezbędne jest wyznaczenie pełnej liczby odłożeń fali λ w odległości satelita - odbiornik (inicjalizacja odbiornika)
4 niewiadome X, Y, Z, ΔtA
Obserwacje 4 satelitów rozwiązują problem
Współrzędne punktu mogą być obliczone na każdą epokę niezależnie
Pomiary kodowe nadają się do zastosowań w metodzie kinematycznej (nawigacji)
Współrzędne punktu zmieniają się z epoki na epokę
4 niewiadome X, Y, Z, ΔtA oraz niewiadome nieoznaczoności fazy N dla każdego satelity i każdej stacji, np. obserwacja 4 satelitów z 1 stacji zawiera 8 niewiadomych,
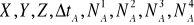
Dla jednej epoki zadanie nierozwiązywalne, zwiększenie liczby obserwowanych satelitów nie rozwiązuje problemu. Dla każdej następnej epoki dochodzi 1 niewiadoma: ΔtA spowodowana chodem zegara odbiornika, np. dla 2 epok mamy 8 obserwacji i 9 niewiadomych
Dopiero dla 3 epok możliwe jest rozwiązanie 12 obserwacji i 10 niewiadomych
Niemożliwe zastosowania kinematyczne, chyba że niewiadome nieoznaczoności fazy zostaną wyznaczone na początku pomiaru na podstawie: obserwacji statycznych lub znanej bazy (wektora) lub zmiany anten i nie występują utraty cykli (cycle slips)
Obserwacja satelitów przez około 30 minut - aż do samoistnej inicjalizacji
Inicjalizacja na bazie - mamy współrzędne 2 punktów, azymut, kierunek, długość - na punktach znajdują się instrumenty. Pomiar inicjalizacyjny trwał około 15 minut.
Metoda kombinowana polegająca na pomiarze na dwóch stanowiskach (około 5 minut) a następnie zamiana anten (czyli przetknięcie wtyczek instrument - antena)
błędy systemu GPS
błędy ośrodka i propagacji sygnału GPS
błędy aparaturowe
błędy wynikające z niewłaściwej geometrii konstelacji satelitów GPS
błędy stosowanych technologii
błędy orbit wynikające z
błędów znajomości pola grawitacyjnego
błędów ekstrapolacji efemeryd
błędów systemu czasu i transmisji sygnałów przez satelity GPS
degradacja sygnałów satelitów GPS
SA (selective availability)
AS (anti spoofing)
refrakcja jonosferyczna
refrakcja troposferyczna
wielodrożność sygnału
niestabilność częstotliwości generowanej na satelicie i w odbiorniku
błędy centrum fazowego anteny odbiorników (centrum fazowe to punkt gdzie skupia się cały sygnał dochodzący do anteny - stabilność centrum fazowego świadczy o jakości anteny)
błędy zliczania czasu
błędy wyznaczania korelacji (pomiary kodowe) i pomiaru fazy (pomiary fazowe)
Technologia pomiarów statycznych - ważne jest ustalenie właściwej długości obserwacji dla danych odległości między punktami i w zależności od rodzaju sieci.
Technologie szybkich pomiarów statycznych (Fast/rapid static) - ustalenie odpowiedniej długości obserwacji na punkcie przy danej liczbie satelitów.
Technologia DGPS - błędy generacji i transmisji poprawek korekcyjnych
odległość między punktami
stosowana technologia pomiarów GPS
długość obserwacji
harmonogram obserwacji
program (strategia) obserwacji
Wyznaczane współrzędne X, Y, Z
Niezbędny jeden odbiornik GPS
Niska dokładność
Sposób używany zazwyczaj w technologiach kinematycznych (nawigacji) najczęściej przy wykorzystaniu obserwacji kodowych
Wyznaczanie różnic współrzędnych ΔX, ΔY, ΔZ
Niezbędne przynajmniej dwa odbiorniki GPS
Możliwa najwyższa dokładność („centymetrowa” i „milimetrowa”)
Stosowane są metody obserwacji kodowych i fazowych
Sposób najczęściej używany we wszystkich praczach geodezyjnych
Wyznaczanie pozycji bezwzględnej, absolutnej w układzie WGS-84 tzn. współrzędnych (x, y, z), wyznaczane względem środka ciężkości mas Ziemi, korzystamy z 1 instrumentu - niska dokładność, wykorzystywane w nawigacji.
Wyznaczanie pozycji względnej - wyznaczenie wektora swobodnego łączącego 2 stacje (Δx, Δy, Δz), w tym samym układzie WGS-84. Są to obserwacje synchroniczne grupy satelitów GPS, przez co wykorzystujemy 2 lub większą liczbę odbiorników GPS. Obserwacje są obarczone jednakowymi błędami co pozwala na uwolnienie pozycji względnej od wpływu niektórych błędów oraz osłabienie wpływu innych błędów.
statyczne,
kinematyczne,
półkinematyczne,
pseudo statyczne,
pseudo kinematyczne,
szybkie statyczne,
dyferencjalne DGPS.
technologia o największej dokładności,
dwa odbiorniki pozostają stacjonarne podczas całej sesji obserwacyjnej,
możliwe jest zebranie obserwacji z wielu sesji obserwacyjnych,
zebrany materiał poddawany jest opracowaniu po zakończeniu obserwacji (post processing),
długość sesji obserwacyjnych zależy głównie od odległości między punktami i przeznaczenia sieci i wynosi:
minimalna liczba satelitów obserwowanych przez jedną stacje wynosi 4,
minimalna wysokość satelity nad horyzontem 15° ,
odległość pomiędzy stacjami <30 km przy odbiorniku o jednej częstotliwości L1,
dokładność: 1-2 mm.
po ustawieniu odbiornika i anteny ( sprawdzić połączenia)
przed rozpoczęciem pomiaru należy wprowadzić założone parametry obserwacji
po wybraniu z opcji instrumentu odpowiedniej komendy - wciskamy START FAST STATIC SURVEY i
antena do końca obserwacji musi pozostać nieruchoma
odbiornik wyświetla status obserwacji , czas niezbędny do zakończenia obserwacji
podczas całej obserwacji można wprowadzić numer punktu mierzonego i wysokość anteny
gdy czas osiągnie 0 - można zakończyć obserwację , po naciśnięciu MOVE można ruszyć antenę, odbiornik przełącza się ze stanu “static” na “ move”
można przejść na kolejny punkt , ustawić antenę i wcisnąć start itd...
pakiet programów TRIMVEC PLUS firmy Trimble Navigigation, pakiet zawiera trzy zespoły programów: TRIMPLAN, TRIMBLE i TRIMSDB;
pakiet GPSurvey (Trimble);
nie wymagają widoczności optycznej punktów sąsiednich,
nie wymagają budowy kosztownych wież,
bardzo krótki pomiar na stanowisku,
nie zależą od warunków pogodowych,
możliwość wykonywania pomiarów w różnych porach dnia,
bardzo wysoka dokładność - wyższa od pomiarów klasycznych,
położenia pkt. wyznaczane są w jednolitym układzie współrzędnych ( geocentrycznym ),
wyznaczanie pkt. niezależne; nie występuje klasyczne prawo przenoszenia błędów w sieciach,
możliwość wyznaczenia skali i orientacji sieci,
technologie wysoce zautomatyzowane i skomputeryzowane; możliwe sukcesywne opracowywanie wyników, niezbędne jednak gruntowne specjalistyczne przygotowanie użytkowników technologii GPS,
pomiary wysoce ekonomiczne; koszt aparatury zwraca się bardzo szybko,
zakłócenia odbioru sygnałów satelitów w zamkniętym terenie (wysoka zabudowa, las itp.) powodujące tzw. „utratę cykli”,
celowa degradacja sygnału GPS; wprowadzenie degradacji:
brak dostępu użytkowników niektórych krajów do kodu P
te same konstelacje satelitów pojawiają się cyklicznie (co 12h).
wyznaczanie położenia punktów i tworzenie nowoczesnych : globalnych, regionalnych i lokalnych sieci geodezyjnych,
tworzenie osnów dla szybkiego mapowania ( np. met. fotogrametryczna ) i realizacja projektów inżynierskich ( trasowanie linii komunikacyjnych, budowa zapór itp.),
tworzenie sieci punktów oporowych do badania przemieszczeń na obszarach podlegających deformacjom (badanie szkód górniczych i skutków trzęsień Ziemi),
pomiary batymetryczne ( łączne wykorzystanie pomiarów GPS i sondowania),
nawigacja lądowa, morska, lotnicza,
wyznaczanie położenia kamer fotogrametrycznych w momencie wykonywania zdjęć,
wykonywanie niwelacji o dokładności dotychczasowej niwelacji trygonometrycznej i geometrycznej technicznej,
w powiązaniu z pomiarami niwelacji precyzyjnej i grawimetrycznymi wyznaczanie wysokości geoidy,
badanie zjawisk geodynamicznych (pływy, ruch obrotowy Ziemi, ruchy kontynentów itp.).
wyznaczanie położenia pojedynczego punktu (single point positioning) - pomiar jednym odbiornikiem
wyznaczanie poszczególnych linii (cięciw) (baseline concept) - pomiar dwoma odbiornikami
jednoczesne wyznaczenie położenia większej liczby stacji (multistation concept) - pomiar przynajmniej trzema odbiornikami
metoda gwiazdowa
metoda tworzenia zamkniętych figur
Sieć powinna cechować wysoka założona w projekcie dla danego celu dokładność (high accuracy)
Przy zakładaniu sieci musi być uwzględniony czynnik ekonomiczny
Sieć powinna być niezawodna (pewna) tzn. proces zakładanie sieci powinien zapewniać możność wykrywania w sieci błędów grubych i systematycznych.
Jak podzielić wszystkie punkty na mniejsze grupy? Czym się kierować przy podziale?
Jakie stosować technologie? (statyczna, szybka statyczna, kinematyczna, DGPS?)
Czy i do jakich punktów dowiązać mierzoną sieć?
Ile odbiorników/grup obserwacyjnych wykorzystać do pomiaru? Jakie typy odbiorników zastosować? Czy dysponuje jednym typem odbiorników?
Ile czasu będzie trwał pomiar?
Jaką strategię obserwacji zastosować? (kolejność obserwacji, do ilu punktów nawiązywać poszczególne punkty, kolejność pomiaru rozet/gwiazd itp.)
Jak przygotować kosztorys pomiaru sieci?
pomierzona w 1992 r. (pomierzona tylko instrumentami TRIMBLE)
11 punktów (w tym 5 punktów - obserwatoriów - Lamkówko, Borowa Góra, Józefosław, Grybów, Borowiec ).
Kampania zorganizowana przez Centrum Badań Kosmicznych.
Poprzez tę kampanię (1992r.) został spełniony warunek przystąpienia do NATO
1993 r. sieć podstawowa ZTWP/DMA - pomierzono53 punkty zerowego rzędu (służba wojskowa Polski ZTWP zawarła umowę ze służbą wojskową amerykańską DMA)
zaakceptowano obliczenie współrzędnych włączonych do układu natowskiego (WGS 84)
1994-1996 r. pomiar sieci podstawowych GPS:
wojskowa -550 punktów (usytuowanych przy drodze, o łatwym dostępie, umożliwiający szybkie dotarcie metodami naziemnymi - TOTAL STATION; sieć szczegółowa i nowoczesna; obserwowały ekipy polsko - amerykańskie, obliczenia prowadzono niezależnie w Polsce i Stanach Zjednoczonych. Amerykanie usunęli degradacje sygnału, Wyznaczono współczynniki transformacji elipsoidy Krasowskiego na elipsoidę WGS'84
cywilna POLREF- 360 punktów (sieć cywilna wykorzystuje część punktów sieci klasycznej - nie zawsze przy drodze i o łatwym dostępie, np. na górkach; punkty co 15-25 km). Cywilna służba geodezyjna - współrzędne z ministerstwa.
dziś jest ok. 145 stacji na całym świecie, w tym trzy w Polsce: Józefosław, Borowiec, Lamkówko.
pracują dzień i noc;
codziennie rano pomiary z poprzedniego dnia są przekazywane do centrów.
uzyskuje się:
efemerydy satelitarne precyzyjne
parametry ruchu obrotowego Ziemi (prędkość, nieregularność)
obliczane bardzo dokładnie współrzędne każdej stacji, a także zmiany tych współrzędnych
poprawkę zegara
sieć geodynamiczna
punkty po obu stronach strefy Teisseyre'a - Toniquista
przy przejściu przez strefę T-T poziom geoidy zmienia się w sposób płynny o ok. 4 m.
sieć geodynamiczna, (31 punktów?)
w Polsce 5 punktów: Śnieżka, Grybów, Józefosław, Borowiec, Lamkówko
pomierzona w 1992 r. (pomierzona tylko instrumentami TRIMBLE)
11 punktów (w tym 5 punktów - obserwatoriów - Lamkówko, Borowa Góra, Józefosław, Grybów, Borowiec ).
Kampania zorganizowana przez Centrum Badań Kosmicznych.
Poprzez tę kampanię (1992r.) został spełniony warunek przystąpienia do NATO
zaakceptowano obliczenie współrzędnych włączonych do układu natowskiego (WGS 84)
Wojskowy system nawigacyjny byłego ZSRR, obecnie w administracji Rosji
Konstelacja 24 satelitów (teoretycznie)
3 orbity po 8 satelitów ( w odległości 45°)
Orbity
Każdy satelita transmituje sygnał o innej częstotliwości (a więc inaczej niż GPS)
Częstotliwość L1 wynika z następującej zależności
Częstotliwość L1 i L2 są związane zależnościami
Wszystkie satelity GLONASS transmitują taki sam kod, ale na innej częstotliwości
Każdy satelita GLONASS nadaje precyzyjne pozycje na pełne półgodziny (podczas gdy GPS ciągle)
Sygnały są odniesione do systemu czasu UTCSU (Uniwersalny Czas Koordynowany byłego Związku Radzieckiego)
Współrzędne satelity podawane są w układzie współrzędnych SGS85 (Soviet Geodetic System 85)
GLONASS rozpoczął prace 12 października 1982
Sygnały są odniesione do systemu czasu UTCSU (Uniwersalny Czas Koordynowany byłego Związku Radzieckiego)
Współrzędne satelity podawane są w układzie współrzędnych SGS85 (Soviet Geodetic System 85)
odwrotność : w systemie GPS - stała częstotliwość i różne kody, zaś w systemie GLONASS - zmienna częstotliwość i stałe kody
bardzo wysokie dokładności,
nieprzerwane działania w czasie rzeczywistym
pewności że otrzymywane sygnały satelitarne są poprawne
Dokładność (accuracy) - GPS nie może zapewnić wymaganej dokładności, szczególnie dla nawigacji lotniczej w fazie lądowania; pojedynczy odbiornik GPS zainstalowany na pokładzie samolotu może bowiem wyznaczyć pozycję z dokładnością jedynie kilkunastu metrów. Należy w tym przypadku stosować którąś z technik pomiarów różnicowych, np. DGPS. Pewnym rozwiązaniem jest tu zorganizowanie specjalnego systemu LAAS (Local Area Augmentation System).
Zdolność natychmiastowego ostrzegania użytkownika o niewłaściwym funkcjonowaniu (integrity). Jest to jeden z podstawowych warunków - ważnych szczególnie dla lotnictwa cywilnego którego nie spełnia amerykański system GPS. Wprawdzie sygnały poszczególnych satelitów GPS zawierają informację o poprawności ich działania (satelitle heath), ale użytkownik nie jest informowany o poprawności działania całego systemu i ostrzegany, że w danej chwili nie powinno się z niego korzystać. Taka informacja powinna dotrzeć do użytkownika w ciągu kilku sekund od chwili powstania awarii sytemu. Spełnienie warunku integrity jest bardzo trudne i stosuje się do tego dwie metody: tzw. wewnętrzne lub zewnętrzne. Metoda wewnętrzna bywa nazywana RAIM (receiver autonomous integrity monitoring). Polega ona na wykorzystaniu pomiarów wykonanych przy użyciu nadliczbowych satelitów i niestety nie daje pewnych wyników. Administratorzy systemów satelitarnych rozwijają raczej metody zewnętrzne (external methods of integrity monitoring) polegające na kontroli w czasie rzeczywistym sygnału systemu przez specjalną sieć stacji naziemnych. Dodatkowym kanałem (GPS integrity channel GIC) wysyłany jest do użytkownika GPS niezależny sygnał zawierający informację integrity. Do jego transmisji najczęściej wykorzystuje się satelity geostacjonarne, np. Inmarsat. Innym - przyszłościowym rozwiązaniem w metodach zewnętrznych będzie łączone wykorzystanie sygnałów systemu GPS i sygnałów pochodzących z niezależnych źródeł, np. pomiarów inercyjnych, Loran C, GLONASS czy Galileo.
Dostępność systemu (availability). Jest to współczynnik wyrażający w procentach czas, w ciągu którego system może być wykorzystywany. Amerykańska organizacja FAA (Federal Aviation Administration) żąda, aby ten czas nie był krótszy niż 99,999% dla nawigacji w korytach powietrznych, podczas zbliżania do lotnisk i lądowania oraz dla nadzoru lotniczego. Aby zapewnić dostępność satelitarnego systemu wyznaczania pozycji i czasu stosuje się różne sposoby. Jednym z nich jest budowanie i rozwijanie systemów wspomagających (augmentation systems). I tak, w Stanach Zjednoczonych utworzono WASS (Wide Area Augmentation System), w Europie działa już EGNOS (European Geostationary Navigation System), w Japoni powstał system MSAT (Multi-functional Satellite-based Augmentation Sernice), w Chinach zaś - SNAS (satellite Navigation Augmentation System). Ich cechą wspólną jest silnie rozbudowana sieć kontrolnych stacji naziemnych, które obserwują wszystkie widoczne satelity GPS (GLONASS), rejestrują wysyłane przez nie sygnały dwuczęstotliwościowe i dane meteorologiczne oraz na ich podstawie wyznaczają precyzyjne poprawki do efemeryd satelitów GPS i poprawkę zegarów satelitów. Poprawki te wraz z sygnałem zawierającym informację integrity przesyłane są poprzez satelitę geostacjonarnego do użytkownika.
Nieprzerwane funkcjonowanie systemu (continuity of service). Warunek ten określa zdolność systemu satelitarnego do zapewnienia żądanego serwisu przez określony czas bez jakichkolwiek przerw. Również on jest bardzo ważny dla lotniczych zastosowań, szczególnie w fazie startu i lądowania.
Proceduress - sposób sprawowania kontroli i atestowania systemu (control procedures & Attestation)
<3 m: dokładność odbiornika odbierającego sygnał WAAS/EGNOS.
5-3 m: taki przedział dokładności jest możliwy przy zastosowaniu odbiornika do odbioru sygnału korekcji różnicowej DGPS.
10 m: taką dokładność w praktyce osiągają odbiorniki korzystające z sygnału GPS bez SA.
100 m: to dokładność z jaką odbiorniki określały pozycję do 2 maja 2000 r. kiedy to wyłączono sygnał ograniczający dostęp (SA) do pełnej dokładności.
Systemy lądowania kategorii II i III.
Podejścia do lądowania, także "łamane", jak w MLS kategorii II i III.
Prowadzenie samolotów także po powierzchni lotniska.
SAPOS EPS - pozycjonowanie w czasie rzeczywistym o dokładności 1 - 3 m
SAPOS HEPS - pozycjonowanie w czasie rzeczywisty o dokładności 1 - 5 cm
SAPOS GPPS - pozycjonowanie z geodezyjną dokładnością 1 cm
SAPOS GHPS - pozycjonowanie z najwyższą dokładnością lepszą niż 1 cm
Naziemny (RIMS, MCC, NLES)
Kosmiczny
Użytkownicy
Facility (udogodnienia?)
Zapewnia on niezależność od systemu Rosyjskiego i Amerykańskiego. Dużą wagę przywiązuje się tu do niezależności militarnej.
Europa chce mieć swobodny dostęp do wszystkich komponentów, bez sztucznych ograniczeń dokładności itp.
System ma się nadawać do nawigacji lądowej, morskiej i powietrznej.
Kosmiczny
30 satelitów MEO (Middle Earth Orbit)
Trzy orbity
Wysokość 23000 km
Nachylenie 50°
Dodatkowo 3 satelity stacjonarne
Użytkownicy
Naziemny - segment ten jest rozbudowany. W jego skład wchodzi wiele stacji kontrolujących (głównie warunek integrity) i atestujących.
Bezpłatny dostęp, który pozwala uzyskać dokładność do 10 m
„Subscription service” płatna, średnio dokładna możliwość korzystania z systemu
„Very restricted” - najdroższa ale też i najdokładniejsza możliwość - wykorzystywana przez służby ratownicze, dokładne zadania geodezji
Komisja Europejska UE - odpowiada min. za ogólny kształt systemu, koordynacje z GPS i systemem GLONASS
European Space Agency (ESA) - odpowiada min. za satelity
EUROCONTROL - European Organization for the safety of air navigation - odpowiada za kontrole, testy itp.
Polityczne (suwerenność i niezależność)
Technologiczne (rozwój technologiczny)
Społeczne (lepsza obsługa klientów, zapewnienie bezpieczeństwa transportu)
Ekonomiczne (utworzenie nowych miejsc pracy, wzrost zapotrzebowania na zakup instrumentów itd.)
każdy system będzie administrowany i finansowany niezależnie
kompatybilność systemów
odbiorniki do obu systemów będą sprzedawane bez barier celnych
struktura sygnału GALILEO uwzględnia kryteria bezpieczeństwa narodowego USA
utrzymywanie w aktualności układów współrzędnych
wyznaczanie kształtu Ziemi (włączając morza i oceany, lądy, lód) i zmiany w czasie
wyznaczanie pola grawitacyjnego Ziemi i jego zmian
badanie atmosfery
2. Metody geometryczne i dynamiczne geodezji satelitarnej. Definicje, charakterystyka, przykłady.
geometryczne
- sztuczny satelita Ziemi jest „punktem w przestrzeni”,
- nie wymagana jest znajomość położenia satelity w przestrzeni
(trysferacja, wcięcie przestrzenne nieliniowe, biegunowa).
Metody geometryczne stosowane były w latach 50 i 60-tych . Obecnie natomiast nie mają większego zastosowania. Trudność stanowi wymóg synchronicznych obserwacji z kilku punktów w jednym momencie czasu.
dynamiczne
- sztuczny satelita ziemi jest „czujnikiem” w polu grawitacyjnym (im niższy satelita i ma większą masę tym bardziej reaguje na nieregularność pola grawitacyjnego)
- wymagana jest znajomość położenia SSZ w momencie obserwacji t, czyli:
- położenia i prędkości SSZ lub elementów orbity SSZ w momencie to (początkowym),
-praw rzeczywistego ruchu SSZ (perturbacji) w czasie t-to.
Metody dynamiczne wymagają znajomości orbit (są związane z wyznaczaniem orbit SSZ).
3. Zalety wynikające ze stosowania SSZ.
4. Sztuczne satelity a naturalny satelita Ziemi.
5. Czy naturalny satelita Ziemi może być praktycznie wykorzystany w zastosowaniach geometrycznych i dynamicznych?
Zastosowanie naturalnego satelity Ziemi - Księżyca stwarza pewne problemy:
Jeżeli chcemy wyznaczyć współczynniki pola grawitacyjnego z funkcji zmian elementów orbity w czasie (perturbacje) ![]()
= f(E,C,S,X,Y,Z) , to potrzebne jest dokładne wyznaczenie elementów orbity w różnych odstępach czasu. Księżyc, mniej czuły na niejednorodne pola grawitacyjne, ma perturbacje w sekundach na rok, a SSZ na wysokości 500km w stopniach na dzień.
Ponadto trudność stanowią:
- nieregularność topografii,
- libracja (wahania względem osi),
- niekorzystne jest także stałe nachylenie płaszczyzny orbity Księżyca względem równika.
Wiadomości z teorii ruch sztucznych satelitów Ziemi
1. Definicja ruchu keplerowskiego.
Ruch keplerowski jest ruchem wyidealizowanym, nie istniejącym w rzeczywistości. Ruch keplerowski występowałby gdyby satelita i Ziemia były odizolowane od wpływu innych ciał. W ruchu tym, Ziemia jest sferą jednorodną, a satelita porusza się jedynie pod wpływem sił grawitacyjnych. Jest to tzw. zadanie 2 ciał. Ruch opisuje 6 parametrów stałych w czasie. Ruch ten jest perturbowany, bo działają na niego różne czynniki zakłócające. Jest jednak istotny, bo ruch rzeczywisty (perturbowany) jest jemu bliski.
2. Cechy ruchu Keplerowskiego.
3. Pierwsze prawo Keplera. Wnioski.
Satelita porusza się po orbicie będącej krzywą stożkową, w jednym z ognisk której znajduje się siało centralne (Ziemia).
W sformułowaniu Keplera planety poruszają się po elipsach. Elipsa obok okręgu, paraboli, hiperboli i prostej to jedna z krzywych stożkowych. Krzywe stożkowe powstają z przecięcia stożka płaszczyzną.
Równanie orbity - wywodzi się ono z I prawa Keplera. Przedstawia ono znane z geometrii analitycznej równanie przekrojów stożkowych we współrzędnych biegunowych i z biegunem w ognisku przekroju.
![]()
![]()
- odległość od satelity
λ - wektor Laplace'a
μ - parametr grawitacyjny
e - mimośród ![]()
dla
e = 0 orbita jest kołem
0 < e <1 orbita jest elipsą
e =1 orbita jest parabolą
e > 1 orbita jest hiperbolą
C = 0 orbita jest linią prostą
![]()
- anomalia prawdziwa, kąt między kierunkiem perygeum a kierunkiem na satelitę
p - parametr orbity ![]()
, jednocześnie odległość od satelity gdy ![]()
C - wektorowa całka pola
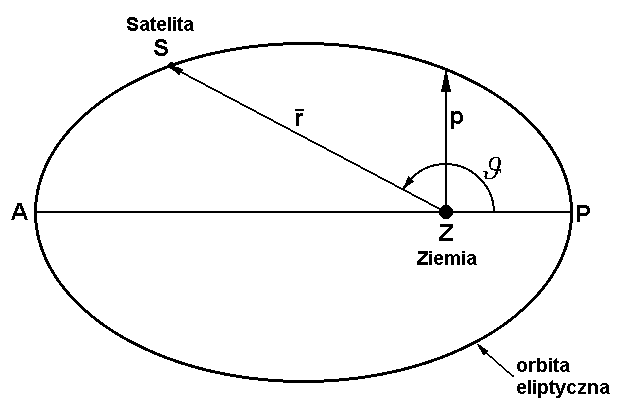
P - perygeum
A - apogeum
4. Drugie prawo Keplera. Wnioski.
Można je sformułować różnorako:
![]()
gdzie:
![]()
- współczynnik proporcjonalności
tp - czas przejścia przez perygeum (lub inny punkt początkowy)
![]()
Wniosek: Prędkość kątowa ![]()
satelity zależy od odległości od ciała centralnego (nie jest stała)
![]()
5. Trzecie prawo Keplera. Wnioski.
Kwadraty okresów obiegu dwóch satelitów wokół ciała centralnego (Ziemi) są proporcjonalne do trzecich potęg ich średnich odległości od ciała centralnego.
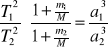
gdzie:
m1,m2 - masy satelitów
M - masa ciała centralnego
Z trzeciego prawa Keplera wynika, że satelity o większej masie mają okres obiegu T krótszy niż satelity o masie mniejszej.
6. Rodzaje orbit sztucznych satelitów.
Wyróżniamy następujące rodzaje orbit
Orbita kołowa e = 0
Orbita eliptyczna 0 < e <1
Orbita paraboliczna e =1
Orbita hiperboliczna e > 1
Istnieje jeszcze jeden przypadek, dla C = 0 orbita jest linią prostą
Charakter orbity zależeć będzie od prędkości początkowej, jaką nadamy satelicie znajdującemu się na pewnej wysokości ponad powierzchnią Ziemi.
I tak dla:
7. Definicje:
Perigeum - punkt orbity, w którym odległość od ciała centralnego (Ziemi) jest najmniejsza. W punkcie tym anomalia prawdziwa ϑ = 0.
Apogeum - punkt orbity, najbardziej oddalony od ciała centralnego (Ziemi) ϑ=180.
Linia apsyd - punkty apogeum i perigeum nazywa się również apsydami orbity, linia łącząca te punkty nazywana jest linią apsyd.
Węzeł wstępujący orbity - pkt. orbity, w którym satelita poruszający się po orbicie z południa na północ przecina płaszczyznę równika.
Węzeł zstępujący orbity - pkt. orbity, w którym satelita poruszający się po orbicie z północy na południe przecina płaszczyznę równka.
Linia węzłów - linia przecięcia płaszczyzny orbity z płaszczyzną równika ziemskiego.
Argument perigeum ω - odległość kątowa punktu perigeum P od węzła wstępującego orbity, liczona w kierunku od węzła, w płaszczyźnie orbity zgodnie z ruchem satelity.
Argument szerokości u - odległość kątowa satelity od węzła wstępującego, stanowiąca sumę u=ω+ϑ (argumentu perigeum i anomalii prawdziwej).
8. Definicje:
anomalia prawdziwa ![]()
, kąt między kierunkiem perygeum a kierunkiem na satelitę
anomalia mimośrodowa E (ekscentryczna) - jest to kąt pomiędzy kierunkiem do punktu perigeum P a kierunkiem do rzutu (prostopadłego lub równoległego do linii apsyd) położenia satelity na koło opisane lub wpisane w orbitę.
anomalia średnia M - stanowi ona odległość kątową od perigeum orbity punktu fikcyjnego, poruszającego się jednostajnie ze stałą prędkością kątowo n. Dana jest wzorem ![]()
, gdzie t - moment przejścia satelity przez dany punkt orbity, tp - moment przejścia satelity przez perigeum orbity, n - średnia prędkość satelity.
9. Równanie ruch SSZ. Całkowanie równania ruchu. Wylicz całki jakie możemy otrzymać?
Równanie ruchu satelity jest równaniem różniczkowym drugiego rzędu określające ruch satelity względem ciała centralnego. Dzięki temu równaniu można wyznaczyć, w dowolnym momencie, położenie i prędkość satelity. Równanie to ma postać:
gdzie:
![]()
to druga pochodna ![]()
wektora ![]()
μ - parametr grawitacyjny
Parametr grawitacyjny ![]()
. Jeśli w równaniu uwzględnia się wpływ oddziaływania satelity na ciało centralne to mamy do czynienia z zadaniem ogólnym 2 ciał. Jeśli się tego wpływu nie uwzględnia to ![]()
i taki przypadek nosi nazwę zadania ograniczonego.
Siła, z którą ciało o dużej masie przyciąga małe ciało, jest zgodnie z trzecią zasadą dynamiki Newtona dokładnie równa sile, z jaką małe ciało przyciąga ciało o dużej masie. Jednak siła, z jaką małe ciało przyciąga ciało o dużej masie, wywołuje nieistotne, niewidoczne w skutkach przyspieszenia. Pod wpływem tej siły położenie ciała o dużej masie nie ulega praktycznie żadnej zmianie i dlatego siłę tę w rozważaniach można praktycznie zaniedbać.
Całkowanie równania ruchu powoduje wprowadzenie dwóch wektorów stałych ![]()
i ![]()
.
Pierwsze całkowanie równania ruchu satelity daje wektor ![]()
. Wektor ten nazywa się stałą wektorową pola.
![]()
Powyższy wzór przedstawia tzw. wektorową całkę pola. ![]()
jest wektorem prędkości satelity, ![]()
- wektorem odległości satelity od ciała centralnego.
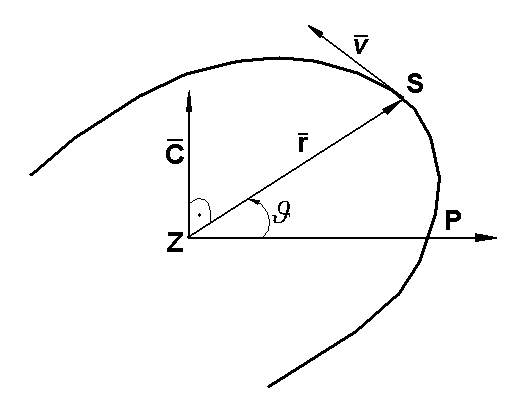
Ze wzoru wynika że ![]()
czyli ruch satelity odbywa się zawsze w jednej płaszczyźnie przechodzącej przez środek masy ciała centralnego. Wektor ![]()
jest do płaszczyzny orbity prostopadły. Płaszczyznę tą tworzę wektory ![]()
i ![]()
. Wektor ![]()
wyznacza więc położenie płaszczyzny orbity w przestrzeni.
Jako że wektor ![]()
jest stały, wynika stąd bardzo ważna własność: płaszczyzna orbity keplerowskiej jest stała w czasie i przestrzeni. Z wektorowej całki pola wynika równanie płaszczyzny orbity:
![]()
oraz wzór na prędkość kątową satelity:
![]()
![]()
![]()
ze wzoru tego wynika ważny wniosek, że im satelita znajduje się dalej od ciała centralnego, tym jego prędkość obiegu (kątowa ![]()
) jest mniejsza.
Prędkość poruszania się satelity można wyrazić również przez prędkość polową satelity:
![]()
Jest to jeden ze sposobów zapisu drugiego prawa Keplera. Pozwala to również stwierdzić że prędkość satelity można określić za pomocą stałej ![]()
, która powstaje pośrednio w wyniku pierwszego całkowania równania ruchu satelity.
Pierwsze całkowanie dało wektor ![]()
, drugie daje wektor Laplace'a. Dany on jest wzorem:
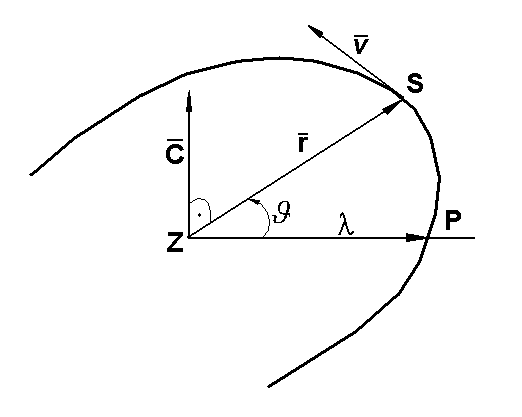
![]()
Wektor Laplace'a skierowany jest skierowany w kierunku punktu perygeum. Wektor ![]()
jest również stały, a więc położenie punktu perygeum jest stałe.
Trzecie całkowanie daje całkę energii .
![]()
Stała h zwana jest stałą energii.
Całkując zależności zadania 2 ciał znaleziono 7 wielkości skalarnych:
Wielkości te nie mogą stanowić ogólnego rozwiązania zadania 2 ciał, gdyż są one zależne:
1) ![]()
, zapisując skalarnie: ![]()
2) ![]()
Z 7 wielkości skalarnych można wziąć dowolnie tylko 5, dwie pozostałe muszą spełniać powyższe warunki.
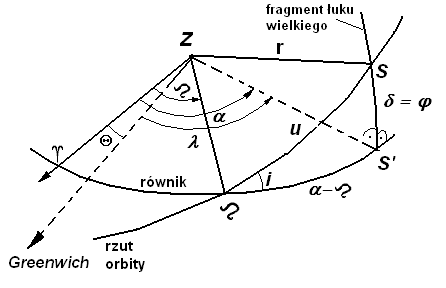
10. Elementy orbity eliptycznej SSZ.
1) Nachylenie orbity względem równika i.
2) Położenie węzła wstępującego N (względem południka Greenwich lub punktu równonocy; jeśli np. jest to położenie względem południka Greenwich to położenie określa długość geograficzna, jeśli jest to położenie względem punktu równonocy - punktu Barana P - położenie określa rektascensja).
3) Położenie orbity w płaszczyźnie - określa je kąt ω.
4) Wielkość orbity, którą określa duża półoś a.
5) Kształt orbity, który określa mimośród e.
6) Określenie czasu t przejścia przez jakiś punkt. Zależnie od satelity, trajektorii toru po jakim się on porusza, kształtu orbity może to być np. perygeum, przejście przez równik.
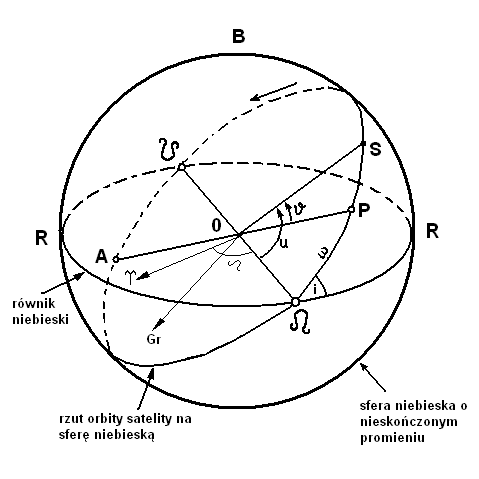
Oznaczenia symboli użytych na rysunku:
u - argument szerokości
ω - argument perygeum
N - węzeł wstępujący - punkt przejścia satelity z półkuli południowej na północną - punkt w którym satelita poruszający się po orbicie z południa na północ przecina płaszczyznę równika
O - węzeł zstępujący - punkt przejścia satelity z półkuli północnej na południową
linia węzłów - linia przecięcia płaszczyzny orbity z płaszczyzną równika ziemskiego
11. Elementy orbity kołowej.
Orbita kołowa jest szczególnym przypadkiem orbity eliptycznej, dla której e = 0. Ruch po orbicie kołowej charakteryzują 4 elementy, a mianowicie: długość lub rektascensja węzła wstępującego orbity N oraz nachylenie orbity i do płaszczyzny równika, które określają położenie płaszczyzny orbity względem przyjętego układu współrzędnych, promień r, określający wielkość orbity i wreszcie czwarty, ostatni element tN - czas przejścia satelity przez węzeł wstępujący.
12. Dyskusja ruchu satelity po orbicie kołowej.
Orbita kołowa jest szczególnym przypadkiem orbity eliptycznej, dla której e = 0.
Parametry określające ruch:
prędkość kołowa
![]()
okres obiegu satelity wokół ciała centralnego
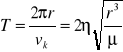
argument szerokości u - odległość kątowa satelity od węzła wstępującego orbity, liczona w kierunku ruchu satelity
13. Dyskusja ruchu satelity po orbicie eliptycznej.
14. Sporządzanie map przelotu satelitów.
Trasa przelotu satelity to rzut geometryczny miejsca punktów kuli ziemskiej, przez zenit których przechodzi satelita. Kształt trasy określają głównie wielkości i oraz T, natomiast zmiany pozostałych elementów orbity, tj.
i tΩ, powodują jedynie przesunięcie trasy w długości geograficznej oraz zmiany położenia rzutu satelity wzdłuż jego trasy.
Różnice długości geograficznych punktów przecięcia orbity satelity z płaszczyzną równika ziemskiego przy dwóch kolejnych jednokierunkowych przelotach satelity nad równikiem nazywa się przemieszczeniem satelity w długości na jeden obieg (przemieszczenie węzła w długości)
![]()
![]()
- doba gwiazdowa
Wartość obliczona będzie nieco odbiegać od faktycznego przemieszczenia w długości ze względu na ustawiczną zmianę położenia płaszczyzny orbity satelity powodowaną różnymi czynnikami, a głównie spłaszczeniem Ziemi.
Przykład trasy przelotu
|
Trasy przelotów satelitów kołowych dla i=65° oraz ΔL = π, 2π, 4π |
Z przedstawionych na rysunku przypadków na szczególną uwagę zasługuje przypadek dla ΔL = 2π. Jak widzimy ze wzoru na ΔL ma on miejsce, gdy T = PG, tzn. gdy satelita obiega Ziemię w ciągu 1 doby gwiazdowej. Trasą przelotu takiego satelity będzie „ósemka”. Gdy ponadto kąt nachylenia orbity wyniesie i = 0°, satelita będzie stale widoczny nad jednym punktem równika. Satelita o opisanych właściwościach jest zwany satelitą stacjonarnym. Satelity takie wykorzystuje się w telekomunikacji, kontroli innych satelitów i obiektów kosmicznych itp.
15. Satelita stacjonarny.
Satelita stacjonarny jest to satelita, który porusza się nad równikiem i=0 na wysokości ok. h=36000km nad Ziemią, jego okres obiegu T=24h, a więc znajduje się zawsze nad tym samym punktem równika (satelity telekomunikacyjne, obserwujące inne satelity, itd.).
16. Obliczenie parametrów niezbędnych do instalacji anteny satelitarnej.
![]()
![]()
gdzie:
λ0 - dł. geograficzna satelity
λ,ϕ - dł. i szer. geograficzna miejsca, w którym chcemy zainstalować antenę
R0 - odległość do satelity
R - promień Ziemi 6370km.
17. Pierwsza, druga, trzecia prędkość kosmiczna.
I prędkość kosmiczna - minimalna prędkość jaką należy nadać satelicie na powierzchni ciała centralnego aby mógł on oderwać się od tego ciała i poruszać się po jego powierzchni po orbicie kołowej.
![]()
Dla Ziemi jest to 7,9 km/sek.
II prędkość kosmiczna - minimalna prędkość jaką należy nadać na powierzchni ciała centralnego, aby mógł on opuścić sferę przyciągania tego ciała.
Druga prędkość kosmiczna jest to zatem prędkość paraboliczna na powierzchni tego ciała:
![]()
Dla Ziemi jest to 11,2 km/sek. Sztuczny satelita Ziemi, któremu nadano II prędkość kosmiczną opuści sferę przyciągania Ziemi lecz zostanie przychwycony przez Słońce i stanie się jego sztucznym satelitą
III prędkość kosmiczna - minimalna prędkość jaką należy nadać satelicie na powierzchni ciała centralnego, wystarczająca do tego aby przy sprzyjających warunkach mógł on opuścić słoneczny układ planetarny.
Dla Ziemi jest to 16.7 km/sek. Sprzyjające warunki oznaczają odpowiednią konfigurację planet, nie zakrzywiającą toru.
18. Równanie Keplera. Zastosowania.
Równanie Keplera pozwala obliczyć moment t przejścia satelity przez dany punkt orbity, znając anomalię mimośrodową odpowiadającą temu punktowi oraz moment tp przejścia satelity przez perigeum orbity. Wielkość n jest średnią prędkością satelity, wielkość zaś ![]()
to anomalia średnia. Stanowi ona odległość kątową od perigeum orbity punktu fikcyjnego, poruszającego się jednostajnie ze stałą prędkością kątowo n.
Równanie Keplera przedstawia się następująco:
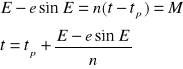
Często mamy do rozwiązania zadanie odwrotne, tzn. należy określić położenie satelity na orbicie w danym momencie t. Położenie satelity na orbicie określają jego współrzędne biegunowe, promień wodzący r i anomalia prawdziwa ![]()
. Ponieważ do obliczenia promienia r, potrzebna jest również anomalia prawdziwa, zatem zadanie takie sprowadza się do wyznaczenia anomalii prawdziwej ![]()
. Najpierw jednak musimy wyznaczyć anomalię mimośrodową z równania Keplera. Niewiadomą E wyznaczamy drogą kolejnych przybliżeń wg ogólnego wzoru:
![]()
Gdzie ![]()
oznaczają kolejne przybliżenia anomalii mimośrodowej. Jako ![]()
można przyjąć M. Znając E obliczamy ![]()
na podstawie wzoru:
![]()
Do obliczenia ![]()
wygodnie jest korzystać z tzw. „równania środka”, które wyprowadza się z równania Keplera przez przedstawienie wielkości E w postaci szeregu trygonometrycznego według potęg e i wielokrotności kąta M. Mamy tu bezpośrednią zależność anomalii prawdziwej od anomalii średniej.
![]()
Równanie Keplera wykorzystujemy do obliczania położenia i prędkości satelity ,gdy mamy dane elementy orbity, oraz do zadania odwrotnego - obliczamy elementy orbity, gdy znamy składowe położenia i prędkości..
19. Współrzędne orbitalne prostokątne i biegunowe satelity.
![]()
- współrzędne prostokątne (układ orbitalny)
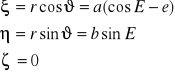
![]()
![]()
- układ przestrzenny
20. Zamiana współrzędnych orbitalnych na współrzędne prostokątne przestrzenne.
Transformacja ta wymaga dokonania 3 obrotów układu ![]()
:
![]()
1. wokół osi 0![]()
o kąt - ω
![]()
2. wokół osi 0 o kąt - i
3. wokół osi 0z o kąt -
21. Obliczanie współrzędnych prostokątnych przestrzennych i prędkości satelity na podstawie elementów orbity. Zadanie odwrotne.
Mamy dane:
![]()
- parametr grawitacyjny
- kąt liczony od obranego stałego kierunku (np. od punktu równonocy P, lub południka Greenwich) do kierunku węzła wstępującego
i - nachylenie orbity względem równika
ω - argument perygeum
a, e - wielkość i kształt orbity
tp - czas przejścia przez perigeum
t - czas dla którego liczymy położenie i prędkość
Kolejność obliczeń:
1.
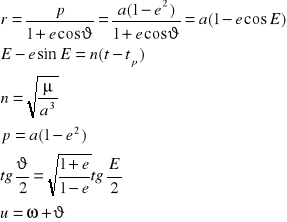
2.
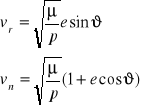
3. Obliczenie współrzędnych i składowych prędkości
22. Podział sił (czynników) perturbujących ruch SSZ.
SIŁY POTENCJALNE
INNE CZYNNIKI
Wszystkie te czynniki sprawiają że obliczanie i uwzględnianie perturbacji przy wyznaczaniu aktualnych elementów orbit jest rzeczą trudną i bardzo skomplikowaną.
23. Korzyści płynące z podziału sił perturbujących na potencjalne i niepotencjalne.
24. Ogólna postać wzorów Gaussa, Lagrange'a i Kauli. Jak i kiedy wykorzystujemy te wzory.
Równania Gaussa
Równania te wyrażają zmienione elementy orbity (perturbacje) jako funkcję tej orbity i składowych sił perturbujących. W zależności od składowych siły wyróżniamy dwa rodzaje równań (postać ogólna):
I rodzaj
![]()
gdzie R,S,W to składowe siły perturbującej:
R - wzdłuż promienia wodzącego satelity o zwrocie dodatnim w kierunku od ciała centralnego (składowa radialna)
S - wzdłuż kierunku prostopadłego do promienia wodzącego w płaszczyźnie oskulacyjnej orbity o zwrocie zgodnym z kierunkiem ruchu satelity (składowa transwersalna)
W - wzdłuż kierunku prostopadłego do płaszczyzny orbity oskulacyjnej o zwrocie takim, aby układ RSW był prawoskrętny (składowa ortogonalna).
II rodzaj
![]()
gdzie T, N, W to składowe siły perturbującej:
T - wzdłuż kierunku stycznego do orbity o zwrocie zgodnym z kierunkiem ruchu satelity (składowa styczna, tangencjalna)
N - wzdłuż kierunku prostopadłego (normalnego) do orbity, o zwrocie dodatnim w kierunku ciała centralnego (składowa normalna)
W - wzdłuż kierunku prostopadłego do płaszczyzny orbity oskulacyjnej (chwilowej) o zwrocie takim, aby układ TNW był prawoskrętny (składowa ortogonalna).
Wzory Gaussa można wykorzystać do każdej siły perturbującej. Możemy na przykład zbadać jak opór atmosfery wpływa na elementy orbity. W tym celu bierze się wyrażenie na opór atmosfery, rozbija na składowe np. T, N, W . Następnie wstawia się je do konkretnego wzoru w zależności zmianę którego elementu orbity chcemy określić.
Równania Lagrange'a
Ważnym przypadkiem szczególnym równań Gaussa są równania Lagrange'a, mające zastosowanie wówczas gdy siła zakłócająca F jest siłą potencjalną o potencjale R (potencjał zakłócający), czyli gdy F = grad R. przypadek ten jest często spotykamy, gdyż większość najważniejszych sił perturbujących ruch sztucznego satelity stanowią siły potencjalne, np. wszystkie siły grawitacyjne, a wśród nich siły pochodzące od niecentralności pola grawitacyjnego Ziemi, wpływu Księżyca i Słońca, wpływu innych planet itp.
Wzory Lagrange'a są to równania wyrażające perturbowane elementy orbity w funkcji samych elementów orbity i pochodnych potencjału zakłócającego względem elementów orbity. Postać ogólna wzorów przedstawia się następująco:
![]()
Składowe potencjalnej siły perturbującej R, S, W są pochodnymi funkcji R w odpowiednich kierunkach:
![]()
![]()
![]()
Wzory Kauli
Stosowanie wzorów Lagrange'a wymaga obliczenia różniczek potencjału zakłócającego względem elementów orbity. Z tego względu, jest bardzo korzystne aby potencjał zakłócający R był przedstawiony w funkcji wszystkich elementów orbity. Ułatwi to obliczenie potrzebnych różniczek. Odpowiednim przekształceniem wzorów dla potencjału zakłócającego zajmowało się wielu naukowców, jednak najlepiej udało się to Kauli.
Wzory te przedstawiają się następująco:
![]()
![]()
- wzór masakra, i tak nikt by się go nie nauczył
25. Perturbacje wiekowe, długookresowe, krótkookresowe i dobowe. Definicje, okresy.
PERTURBACJE WIEKOWE
Mówimy o nich, gdy dokonujące się zmiany elementów są proporcjonalne do czasu. Wyróżniamy tu perturbacje wiekowe pierwszego rzędu t lub perturbacje wiekowe wyższych rzędów tn. Dzięki analizie perturbacji wiekowych można zbadać i wyznaczyć grawitacyjne pole Ziemi.
PERTURBACJE WIEKOWE
- okres tych perturbacji jest równy okresowi obiegu satelity wokół Ziemi.
- funkcje anomalii ![]()
, E, M lub okresu obiegu satelity T itp.
- okres perturbacji równy jednej dobie gwiazdowej
- funkcja czasu gwiazdowego Θ, kata godzinnego t itp.
- okres równy okresowi obiegu punktu perigeum wokół orbity
- funkcja argumentu perigeum ω
26. Praktyczne znaczenie podziału perturbacji na wiekowe, długo- i krótkookresowe.
27. Perturbacje orbit SSZ spowodowane polem grawitacyjnym Ziemi.
Perturbacje spowodowane ziemskim polem grawitacyjnym
Perturbacje te można analizować wykorzystując wzory Kauli, przedstawiające grawitacyjny potencjał zakłócający w funkcji elementów orbity i współczynników rozwinięcia tego w szereg funkcji kulistych. Ziemskie pole grawitacyjne powoduje perturbacje wiekowe, długookresowe i krótkookresowe.
Perturbacje spowodowane spłaszczeniem Ziemi
Spłaszczenie Ziemi jest jednym z najistotniejszych czynników powodujących zakłócenia ruchu keplerowskiego bliskich satelitów. Spłaszczenie Ziemi powoduje znaczne zmiany położenia płaszczyzny orbity w przestrzeni i położenia orbity w jej płaszczyźnie, natomiast kształt i rozmiary orbity pozostają praktycznie nie zmienione.
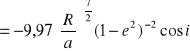
1°/ 1 dobę śr.
Ze wzoru wynika, że obrót linii węzłów następuje tym szybciej, im kąt nachylenia orbity do równika jest mniejszy. Dla satelitów biegunowych (i = 90°) zjawisko precesji płaszczyzny orbity praktycznie nie występuje. Dla satelitów o małym kącie nachylenia orbity (prawie równikowych) przemieszczenie się węzła wstępującego odbywa się bardzo szybko i dla satelitów poruszających się na wysokości około 1000km prędkość obrotu linii węzłów może wynosić 6°/dobę.
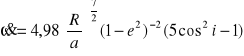
1°/ dobę śr.
Dla i1 = 63°26′ lub i2 = 116°34′ (tzw. wartości krytyczne) ruch perigeum nie występuje ![]()
= 0. Dla i < i1 lub i > i2 ![]()
> 0, kierunek ruchu perigeum jest zgodny z kierunkiem ruchu satelity. Dla i1 < i < i2 ![]()
< 0, kierunek ruchu perigeum jest przeciwny do kierunku ruchu satelity. Dla H = 1000 km, i = 0° ![]()
≈ 12°/ dobę śr.
28. Perturbacje orbit SSZ wywołane oporem atmosfery.
Opór atmosfery jest jednym z najsilniej działających zakłóceń ruchu niskich satelitów i objawia się tym silniej im satelita porusza się niżej, tzn. w gęstszych warstwach atmosfery. Jako dolną granicę możliwości swobodnego poruszania się satelity przyjmuję się 150 km nad powierzchnią Ziemi; poniżej tej granicy poruszający się satelita ulega spaleniu po kilku okrążeniach Ziemi. W miarę oddalania się satelity od Ziemi gęstość atmosfery szybko maleję tak, że górną granicę praktycznego wpływu oporu powietrza na ruch satelity stanowi wysokość około 1000 km nad powierzchnią Ziemi. Działanie oporu powietrza na satelitę ma narastający charakter wiekowy i prowadzi do istotnej zmiany kształtu orbity SSZ.
28. Paradoks ruchu satelity.
Prędkość obiegu satelity poruszającego się po prawie kołowej orbicie na skutek oporu atmosfery zwiększa się, zaś przyśpieszenie satelity jest równe sile oporu powietrza, przypadającemu na jednostkę masy satelity. Oznacza to, że z dwóch satelitów poruszających się na tej samej wysokości ten będzie poruszał się szybciej, na który działa większa siła oporu powietrza.
Techniki obserwacyjne SSZ.
1. Klasyfikacje metod obserwacji SSZ.
Technik optyczne
fotograficzna
laserowa
Techniki elektroniczne
dopplerowska
GPS
altimetria
VLBI
Charakterystyka technik ze względu na dokładność oraz elementy mierzone.
Fotograficzna - w technice tej wyznacza się kierunek do satelity, a więc otrzymuje się współrzędne równikowe ( - rektascensja, δ - deklinacja) satelity w danym momencie. Dokładność wyznaczenia - maksymalnie 1” - 0.5”. Technika ta jest już nieużywana.
Laserowa - mierzy się tu odległość do satelity za pomocą dalmierza laserowego. Jest to jedna z najdokładniejszych technik, dokładność pomiaru dochodzi tu do 3 cm. Wadą metody jest jej stacyjność - aparatura pomiarowa waży około 1 - 2 ton. W Polsce jest jedna tylko stacja w Borowcu pod Poznaniem. Dalmierz laserowy tej stacji został zbudowany samodzielnie przez jej pracowników.
Dopplerowska - tą technika wyznaczane były głównie różnice współrzędnych x, y, z między stacjami pomiarowymi. Możliwe też było bezpośrednie wyznaczenie współrzędnych, ale ze względu na zdecydowanie mniejszą dokładność było rzadziej stosowane. Dokładność metody to 30 - 40 cm, dla odległości pomiędzy punktami (stacjami) 400 km. Technika ta jest już nieużywana, jednak, ze względu na jej liczne podobieństwa z GPS, warto ją poznać.
GPS - w tej technice z pomiarów odległości do satelity wyznacza się albo współrzędne albo różnice współrzędnych. Dokładność zależy od potrzeb, mogą to być zarówno metry jak i milimetry.
Altimetria - technika pomiarów wysokości nad obszarem mórz, czyli wyznaczenia wysokości satelity nad poziomem morza. Dokładność metody to kilka centymetrów. Pomiar wykonuje się na obszarze o promieniu kilometra w wielu punktach, a następnie sprowadza do punktu środkowego. Ma to za zadanie zwiększyć dokładność poprzez wyeliminowanie lokalnych nierówności np. fal. Dzięki tej technice można wyznaczyć profile geoidy, a więc jej wysokość.
VLBI - very long base interference (interferencja długich baz). Technika ta jest wykorzystywana do celów geodezyjnych i geodynamicznych. Wykorzystuje promieniowanie radiowe wysyłane z kosmosu. Dokładność ok. 4 - 5 cm. W Polsce jest jedna baza wykorzystująca tą technikę, w Piwnicach pod Toruniem.
2. Zasada metody fotograficznej. Etapy prac.
W technice fotograficznej obfotografowywało się obraz satelity na tle gwiazd. Tor po którym poruszał się satelita, był na zdjęciu linią przerywaną (zastosowanie tarczy ze szczeliną). Dzięki temu można wyznaczyć położenie satelity w danym momencie czasu. Wywołanie zdjęcia zajmowało około 5 dni. Proces ten należało przeprowadzić powoli by nie nastąpiły skurcze ani deformacje (np. pod wpływem zmiany temperatury). Gdy miało się gotowe zdjęcie, należało zidentyfikować na nim obfotografowane gwiazdy, oraz dla tych które mają - ustalić współrzędne i δ (są to tzw. gwiazdy oporowe). Następnie w urządzeniu zwanym koordynometrem mierzyło się, w lokalnym układzie współrzędnych xy, współrzędne gwiazd oporowych i współrzędne satelity. Znalezienie współrzędnych i δ satelity następowało przez transformacje. Gwiazdy oporowe, dla których znamy zarówno współrzędne lokalne (x,y) jaki i równikowe (,δ), pełniły tu role punktów łącznych.
Etapy prac
Pełne opracowanie zajmowało około 5 miesięcy. Metoda miała jedną istotną zaletę, mianowicie otrzymywano dzięki niej współrzędne równikowe - czyli współrzędne odniesione do jednego układu na całym świecie.
3. Rodzaje satelitarnych kamer fotograficznych.
kamery 2 - osiowe (balistyczne) - często były to po prostu teodolity, które zamiast lunety miały kamerę np. BC - 4 Wild
śledzące:
kamery 3 - osiowe (paralaktyczne) - miały możliwość kompensacji ruchu obrotowego dobowego Ziemi
kamery 4 - osiowe - miały możliwość kompensacji ruch satelity po mały kole - satelita obfotografowywał się jako punkt
W Polsce używano dwóch typów kamer Zaiss SBG i AFU - 75. Było po 4 - 5 egzemplarzy każdego.
4. Dokładność satelitarnych pomiarów fotograficznych.
Dokładność pomiaru dla większości precyzyjnych kamer wynosi 1-2'. Niektóre kamery posiadają dokładność pomiar współrzędnych jasnych satelitów 0,5-2”, a dla satelitów słabych (przy obserwacji dodatkowo specjalny sposób kompensacji ich ruchu) wacha się 2-4”. Dokładność rejestracji czasu, odpowiadającego momentowi wykonania zdjęcia wynosi 0,1-0,5 msek.
Dokładność tej metody warunkują błędy instrumentalne kamery i wpływy atmosferyczne, głównie refrakcji.
5. Zalety pomiarów fotograficznych.
dokładność pomiarów fotograficznych : dokładność pomiaru kierunku (α,γ) 0,5” -2” dla jasnych satelitów, 1”-2” dla słabych satelitów, czas wykonania zdjęcia- 0,1-0,5msek)
WADA-możliwe do stosowania tylko wtedy, gdy są dobre warunki atmosferyczne i satelita oświetlony światłem słonecznym ,i gdy Słońce znajduje się dostatecznie nisko nad horyzontem.
6. Zasada metody laserowej pomiaru odległości do satelity.
Przy pomiarze metodą laserową realizowany jest następujący wzór:
d = (Δt/2) c
gdzie:
Δt - jest to czas przebiegu impulsu laserowego od momentu wysłania do powrotu do odbiornika, po odbiciu od reflektora na satelicie
d - mierzona odległość
c - prędkość światła.
Dokładność pomiaru w tej metodzie zależy od:
Długość impulsu 1ns (10 -9 s) daje dokładność odległości ok. 15 cm.
7. Generacje satelitarnej aparatury laserowej.
|
długość impulsu |
dokładność pomiaru |
uwagi |
1 generacja |
10 - 40 ns |
1 - 6 m |
lasery rubinowe |
2 generacja |
2 - 5 ns |
0.3 - 1 m |
lasery rubinowe, zastosowanie urządzeń pulsacyjnych |
3 generacja |
0.1 - 0.2 ns (100 - 200 ps) |
1 - 3 cm |
Najczęściej lasery Nd:YAG (grant itrowo-aluminiowy z domieszką neodymu), zdolność do analizy poszczególnych fotonów |
8. Zastosowania pomiarów laserowych.
9. Zasada satelitarnej metody dopplerowskiej wyznaczenia położenia punktów.
Technika wykorzystuje efekt Dopplera, czyli zmianę częstotliwości, gdy źródło i odbiornik są w ruchu. Satelita, poruszając się po orbicie, zmienia swoją odległość od obserwatora, a więc ma prędkość radialną. Na podstawie różnicy (fs - fr) między częstotliwością wysyłaną przez satelitę a odbieraną na Ziemi, można określić tą prędkość. Znając dodatkowo przedział czasu, można wyznaczyć różnicę odległości satelity od odbiornika (różnice w odległości powstałą w tym przedziale czasu). Wzór przedstawiający tą zależność ma postać:
![]()
Gdzie ![]()
to prędkość radialna czyli pochodna drogi po czasie. Licznik we wzorze to różnica odległości, mianownik to przedział czasu. Z kolei c we wzorze to prędkość światła (jest to pewne uproszczenie, gdyż ze względu na atmosferę prędkość ta jest trochę inna).
Satelita dopplerowski wyposażony jest w aparaturę, która nadaje sygnał o częstotliwości fs. Częstotliwość ta jako zmieniona fr dochodzi do odbiornika. Tu następuje generowanie podobnej, wysokostabilnej częstotliwość f0. Częstotliwości te porównuje się poprzez nałożenie, w wyniku którego powstaje częstotliwość dudnienia. Miarą różnicy częstotliwości f0 - fr (nie mylić z fs - fr) jest liczba okresów częstotliwości dudnienia N. Wartość ta jest liczba całkowitą i jest dana wzorem:
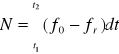
Wzór ten jest podstawą skonstruowania aparatury pomiarowej. Satelita nadaje sygnał w sposób ciągły. Aparatura zlicza różnice (całkuje) w przedziale czasu t2 - t1 i podaje N. Przedział czasu t2 - t1 wynosi zazwyczaj 120 sekund. O tym w którym momencie dany cykl całkowania się zaczyna i w którym kończy informuje sygnał czasu przekazywany przez satelitę. W chwili zakończenia jednego zliczania automatycznie rozpoczyna się kolejne (system jest ciągły). Różnice odległości do satelity, w dwóch jego położeniach, są wyznaczane właśnie dla tego 2 minutowego okres czasu. Żeby różnice tą przedstawić w postaci wzoru, należy wykorzystać zależności wynikające z dwóch wyżej przedstawionych wzorów. Po przekształceniach dostajemy gotowy wzór:
![]()
Gdzie N to liczba okresów częstotliwości dudnienia, znana z pomiaru. Indeksy przy niej oznaczają: i - stanowisko obserwatora, jk - położenia satelity na orbicie, początkowe (w momencie t1) oraz końcowe ( w momencie t2). Dla dwuminutowych obserwacji N jest rzędu 3-5*106. We wzorze znane są również wartości f0, t (120s) oraz prędkość światła w próżni c. Niewiadoma jest szukana różnica odległości do satelity r oraz f czyli (fs - fr). Różnica ta powinna być w zasadzie stała, ale ze względu na możliwe wahania częstotliwości, przyjmuje się ją jako niewidomą. Powyższy wzór można przedstawić w następującej postaci, która pozwala policzyć współrzędne stacji:
![]()
r zostało tu uzależnione od współrzędnych stacji (xi, yi, zi) oraz współrzędnych satelity w położeniu początkowym i końcowym (xj, yj, zj) i (xk, yk, zk). Znamy współrzędne satelity, natomiast położenie stacji oraz f to niewiadome. Mamy więc cztery niewiadome: xi, yi, zi oraz f. Do ich wyznaczenia potrzebne są więc minimum cztery dwuminutowe pomiary.
10. Efemerydy pokładowe i precyzyjne. Sposoby ich wyznaczania.
Satelita wysyła swoje współrzędne do odbiornika w każdej parzystej minucie. Satelita z kolei otrzymuje te współrzędne ze stacji naziemnych, które wyznaczają je na podstawie znanej orbity. Współrzędne te są wyznaczane są na podstawie ekstrapolacji (znając trasę po której porusza się satelita, wyznacza się trasę po której będzie się dalej poruszał), na pewien czas np. 12h. Są to tzw. broadcast ephemerides (BE) - współrzędne pokładowe, są one obarczone błędem ekstrapolacji. Błędu ekstrapolacji pozbawione są precise ephemerides (PE), które wyznacza się na drodze interpolacji, znając położenie satelity w momencie przed i po obserwacji. Wadą ich jest to, że dostępne są one dopiero kilka dni po obserwacji, a nie jak (BE) w chwili pomiaru.
11. System TRANSIT. Elementy systemu.
Elementy systemu:
Satelity NNSS:
12. Zasada wyznaczenia położenia punktów techniką dopplerowską. (patrz pytanie 9)
13 Wyznaczenie położenia pojedynczego punktu, zasada translokacji i multilokacji.
Translokacja polega na tym że tam sam przelot jest obserwowany jednocześnie przez 2 stacje. Wyznacza się różnice współrzędnych stacji, która jest wolna od błędów, które w jednakowym (lub zbliżonym) stopniu dotykają obie stacje. W tym wypadku wystarczały współrzędne pokładowe. Z multilokacją mamy do czynienia gdy liczba stacji jest większa od 2. Najczęściej używano translokacji.
14. Dokładności wyznaczeń dopplerowskich.
dla metod SSP/BE ~5m
dla metod SSP/PE ~1m
dla metod TL i ML (BE lub PE) 0.3m - 0.5m (przy odległości stacji mniejszej od 400 kilometrów)
SPP - wyznaczenie punktu pojedynczego (single point positioning)
BE - współrzędne pokładowe
PE - współrzędne precyzyjne
TL - translokacja
ML - multilokacja
15. Zasada działania globalnego systemu precyzyjnego GPS.
Po orbitach rozmieszczonych równomiernie nad powierzchnia Ziemi porusza się zespół satelitów (jest to tzw. segment kosmiczny). Współrzędne każdego satelitów, tor po którym się poruszają są znane (może nie zawsze od razu). Odpowiada za to segment kontrolny systemu. Oblicza on tor po którym porusza się każdy satelita, i ogólnie odpowiada za kontrole. Każdy satelita wysyła sygnał. Jeśli odbiornik odbierze sygnał z kilku satelitów to może wyznaczyć swoją pozycje. (podejście bardzo ogólnikowe - więcej w odpowiedzi na następne pytania)
16. Elementy (segmenty) systemu GPS.
Globalny System Pozycyjny został zaprojektowany i skonstruowany w USA na zlecenie amerykańskiego Ministerstwa Obrony, jako globalny wojskowy system nawigacyjny. Składa się on z trzech elementów-segmentów:
Zespół kontrolny (Control Segment) odpowiada za obserwacje satelitów i obliczanie dla każdego satelity precyzyjnych elementów orbity i poprawek pokładowego zegara atomowego (poprawka czasu). Dane te są wprowadzane do pamięci komputerów pokładowych na satelitach. W ten sposób każdy satelita ma aktualizowaną swoją pozycję w przestrzeni i synchronizację swego zegara do czasu całego systemu GPS. Ośrodek dowodzenia systemu GPS (Master Control Stations) znajduje się w bazie amerykańskich sił lotniczych w Colorado Springs. Stacje obserwacyjne (Monitor Stations) pracują w Kwajalein, Diego Garcia, na Wyspach Wniebowstąpienia i na Hawajach. Działa też 6 stacji NGA (National Geospatial Agency) w Argentynie, Australi, Bahrain, Ekwadorze, Stanach Zjednoczonych (US Naval Observtory USNO) i Wielkiej Brytani. Planuje się utworzenie kolejnych stacji. Stacje NGA tworzy się po to, by GPS stał się w pełni systemem nawigacyjnym. Większa ilość stacji naziemnych poza zwiększeniem dokładności wyznaczania efemeryd, służy polepszeniu bezpieczeństwa. Odbywa się to poprzez zwiększenie szybkości i niezawodności działania systemu alarmowego, ostrzegającego o nieprawidłowym działaniu danego satelity lub całego systemu (a jest to warunek konieczny jeśli chce się w pełni wykorzystywać GPS w nawigacji).
Zespół Satelitów (Space Segment) Do prawidłowej pracy systemu wymagane jest minimum 24 satelity. Obecna konstelacja składa się z 29 satelitów umieszczonych na 6 orbitach nachylonych względem równika pod kątem 55° równomiernie rozłożonych w długości geograficznej. Satelity GPS poruszają się po orbitach prawie kołowych oddalonych od powierzchni Ziemi o ponad 20000 km (20200km), okres jednego obiegu takiego satelity wokół Ziemi wynosi około 12 godzin. Oznacza to że dwa razy w ciągu dania pojawia się ta sama konstelacja satelitów. Jest to niezbyt korzystne ze względu na pewne błędy systematyczne. Satelity są widoczne około 5 h nad horyzontem. System jest tak skonstruowany, że w każdym miejscu na Ziemi są naraz widoczne co najmniej 4 satelity. W Polsce można obserwować do 9 satelitów naraz.
Użytkownicy systemu - początkowo było to wojska (US Army), z biegiem czasu system został udostępniony użytkownikom cywilnym.
17. Analiza sygnału satelitów GPS.
Sygnał satelitarny, jaki dociera z satelity do odbiornika jest bardzo skomplikowany. Składa się on z dwóch podstawowych częstotliwości tzw. L1 = 1575.42 MHz i L2 = 1227.60 MHz, na które nałożone są specjalne kody C/A i P oraz cały pakiet różnych informacji. Pomiar prowadzony na dwóch częstotliwościach jest praktycznie wolny od wpływu refrakcji jonosferycznej (refrakcji niższych warstw atmosfery - troposfery eliminuje się poprzez automatyczne wprowadzenie poprawek obliczanych na podstawie przyjętego modelu atmosfery). Częstotliwości nośne (Carrier Frequency) L1 i L2 powstają po pomnożenie częstotliwości generowanej przez zegary na satelicie (Basic Frequency f = 10.23 MHz) przez wartości odpowiednio 154 i 120. Długość fali wynosi około 20 cm.
Na częstotliwość nośną nakładane są kody: C/A (coarse aquisition = clear access) jest to kod ogólnie dostępny i służy do mniej precyzyjnego pomiaru. Kod P (P - code precise = protected) jest kodem precyzyjnym, ale dostępnym nie wszystkim lecz tylko uprawnionym użytkownikom.
Poza tym w sygnale znajdują się inne informacje:
18. Generacje satelitów GPS.
Unowocześnienie systemu GPS - GPS III ma mieć nową generacje satelitów i sygnałów.
19. Degradacja sygnału satelitów GPS. Rodzaje, charakterystyka.
Z chwilą wprowadzenia pełnej operatywności systemu z dniem 1 stycznia 1995 roku wprowadzono również celowe, dawno zapowiadane degradacje sygnału satelitów GPS powodujące zmniejszenie dokładności wyników wyznaczeń bezwzględnej pozycji. W ten sposób Ośrodek Dyspozycyjny systemu GPS ogranicza dostęp i korzystanie z systemu GPS nieupoważnionym użytkownikom. Wprowadzone zostały dwa rodzaje degradacji sygnału GPS. Pierwszy, nazywany selective availability (SA) polega na zniekształceniu poprawki zegarów satelitów GPS i ograniczeniu dokładności elementów orbit zawartych w sygnale satelitarnym. Efektem działania SA było zmniejszenie dokładności wyznaczania pozycji bezwzględnej. I tak przy wyłączonej degradacji dokładność ta wynosiła 15 - 30 m, przy włączonej 150 metrów. Wpływ tej degradacji wyeliminowano poprzez technologie względnego wyznaczania pozycji czyli pomiaru różnicy współrzędnych między stanowiskami. Degradacja S.A. została zniesiona 1 maja 2000 roku. Drugim rodzajem degradacji jest tzw. anti-spoofing (A-S), którego istotą jest zaprzestanie emisji kodu precyzyjnego P i zastąpienie go innym tajnym wojskowym kodem Y. Najnowsze odbiorniki GPS mają specjalne oprogramowanie wewnętrzne umożliwiające taka obróbkę sygnału, która daje możliwość uzyskania dokładnego wyniku pomimo braku kodu P. Użytkownik może instalować w odbiorniku odpowiednie urządzenie AOC - Auxrliary Output Chips albo stosować odbiornik wyposażony specjalny system odbioru i opracowania sygnału (np. cross correlaton, 2 - tracking). Degradacja ta nie szkodzi geodetom, gdyż dokładne współrzędne mogą uzyskać w postprocesingu. Degradacja ta nie zakłóca pracy odbiorników jednokodowych (C/A).
20. Metody pomiarów GPS pseudoodległości i fazowe. Zasada, dokładności, zalety, wady, błędy.
Do wyznaczania pozycji wykorzystywane są pomiary odległości do przynajmniej 4 satelitów, których pozycje w przestrzeni są znane.
System GPS jest tak skonstruowany, oby z każdego punktu na powierzchni Ziemi można było obserwować przynajmniej cztery satelity systemu. Oznacza to, że w każdym momencie możemy pośnieżyć cztery odległości do czterech satelitów, których położenie w przestrzeni jest znane. Położenie anteny odbiornika GPS można wyznaczyć na podstawie przestrzennego liniowego wcięcia wstecz. W zadaniu wyznaczania współrzędnych przestrzennych stanowiska technikami satelitarnymi GPS występują cztery niewiadome, a mianowicie trzy współrzędne X, Y, Z oraz Δt, oznaczający synchronizację zegara odbiornika do czasu systemu GPS. Stąd wynika potrzeba obserwowania czterech satelitów.
Pomiar odległości może być wykonany albo metodą kodową (pomiar pseudoodległości) albo metodą fazową (pomiar fazowy).
Metoda kodowa (pseudoodległości)
W pomiarze kodowym wykorzystuje się fakt, że satelita emituje i odbiornik wytwarza ten sam kod (C/A lub P) w tych samych określonych momentach czasu. Kod, który z sygnałem satelitarnym dociera do odbiornika jest przesunięty w czasie względem kodu wytwarzanego w odbiorniku (tzw. replica code). Przesunięcie to jest miarą czasu, w jakim sygnał dociera z satelity do anteny odbiornika i jest proporcjonalne do odległości Ziemia - satelita. W odbiorniku następuje przesunięcie obu kodów względem siebie aż do uzyskania tzw. korelacji. W ten sposób pomierzony czas przebiegu sygnału z satelity do odbiornika pomnożony przez prędkość rozchodzenia się fal elektromagnetycznych jest równy mierzonej odległości Ziemia - satelita.
W skrócie:
Zasada:
![]()
Dlaczego pseudoodległości?
Na ziemi w przypadku zwykłego dalmierza mierzy się odległość dalmierz - lustro - dalmierz, czyli sygnał jest emitowany i odbierany w tym samym narzędziu. W przypadku metody kodowej, satelita sygnał wysyła, odbiornik odbiera. Pomiar taki ma sens tylko wtedy, gdy dokonana jest dokładna synchronizacja zegarów satelity i odbiornika na ziemi. Przyjęto że taki pomiar (jednostronny!) Ziemia - satelita obarczony w dużym stopniu wpływem błędu niesynchroniczności zegarów na satelicie i w odbiorniku nazywany będzie dla odróżnienia od pomiaru naziemnego wolnego od tego wpływu pomiarem pseudoodległości.
Metoda fazowa
Metoda ta polega na pomiarze fazy sygnału dochodzącego do odbiornika. Mierzona odległość d wyrażana jest w tej metodzie poprzez pewną całkowitą liczbę N pełnych znanych długości fali mieszczącą się w mierzonej odległości plus „końcówka” czyli część pełnej długości fali (faza φ pomnożona przez długość fali λ), co można zapisać elementarnym wzorem:
![]()
Odbiornik GPS umie pomierzyć fazę φ, natomiast główną trudnością tej metody jest wyznaczenie całkowitej liczby N pełnych długości fal mieszczących się w mierzonej odległości d. Jest to problem „nieoznaczoności pełnych cykli długości fal”. Liczbę tę należy dla wszystkich technologii GPS, które operują pomiarami fazowymi wyznaczyć na podstawie specjalnej procedury tzw. inicjalizacji pomiaru. Należy jeszcze dodać, że jeśli nie ma przerwy w łączności z satelitą odbiornik może rejestrować także przedstawioną na rysunku pełną liczbę różnicy całkowitych długości fal Nj - N0 od pewnego momentu początkowego.
W momencie t0 satelita jest w odległości ![]()
gdzie N0 jest niewiadomą liczba odłożeń fali (wyznaczana w procesie inicjalizacji), λ to znana długość fali, φ0 faza mierzona odbiorniku.
W momencie t1 satelita jest w odległości ![]()
. Gdy znamy N0 z momentu t0 możemy wyznaczyć odległość, bo obok φj instrument może mierzyć też wartość (Nj - N0).
W skrócie o metodzie:
Zasada pomiarów fazowych:
![]()
Dokładność pomiarów wykonanych na kodzie C/A wynosi 3m, na kodzie P 30cm, zaś dokładność pomiarów fazowych jest wyższa i wynosi 1.9mm.
21. Równanie obserwacyjne pomiarów kodowych.
Oznaczenia:
i, j, k, l - położenia satelitów
A, B - położenia odbiorników
t* - czas wysłania sygnału przez satelitę (w systemie GPS)
ti - wskazanie zegara satelity i w momencie t*
![]()
- błąd zegara satelity i w momencie t*
tA - wskazanie zegara odbiornika A w momencie odbioru sygnału
![]()
- czas przebycia sygnału od satelity i do odbiornika A
![]()
- błąd zegara odbiornika A w momencie ![]()
tj. w momencie odbioru sygnału
r - obserwacja pseudoodległości
Obserwacja pseudoodległości (pseudo - range)
![]()
Powyższe wyrażenie to model, bo nie uwzględnia błędów. ![]()
to czas przejścia sygnału od satelity do odbiornika. Równanie obserwacji:
![]()
Informacja geodezyjna jest zawarta w wyrazie ![]()
:
![]()
gdzie:
![]()
![]()
- położenie satelity w momencie t
![]()
- położenie odbiornika w momencie t
![]()
- poprawka jonosferyczna
![]()
- poprawka troposferyczna
![]()
- poprawka ze względu na wielodrożność sygnału
![]()
- poprawka ze względu na błędy wynikające z szumu
22. Równanie obserwacyjne pomiarów fazowych.
Oznaczenia:
![]()
- faza oscylatora satelity i w momencie t*
![]()
- faza oscylatora odbiornika A w momencie ![]()
![]()
- nominalna częstotliwość oscylatora satelity
![]()
- długość fali wysyłanej przez satelitę
p - obserwacja fazy
![]()
![]()
N - liczbą pełnych długości fal
Reszta oznaczeń jak w kodowych.
23. Pierwsze, drugie i trzecie różnice pomiarów fazowych. Korzyści, wady, zastosowania.
Pojedyncze różnice

Dwa odbiorniki A, B obserwują jednocześnie położenie satelity i
Definicja pojedynczych różnic obserwacji fazowych:
![]()
![]()
Równania pojedynczych różnic:
![]()
gdzie:
![]()
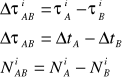
Informacje geodezyjne w wyrazie ![]()
, wyeliminowany wyraz ![]()
Pojedyncze różnice eliminują wpływ błędów zegara satelity.
Podwójne różnice
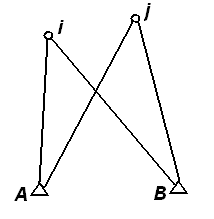
Dwa odbiorniki A, B obserwują jednocześnie położenie satelitów i, j
Definicja drugich różnic obserwacji fazowych:
![]()
![]()
Podwójne różnice = różnice pojedynczych różnic
Równania podwójnych różnic:
![]()
gdzie:
![]()
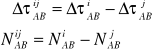
Informacja geodezyjna w wyrazie ![]()
, wyeliminowany wyraz ![]()
Podwójne różnice eliminują wpływ błędów zegarów satelitów i zegarów odbiorników.
Potrójne różnice
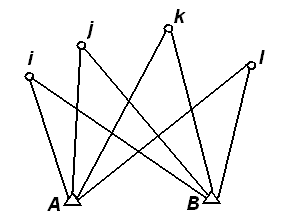
Dwa odbiorniki A, B obserwują jednocześnie położenia satelitów w dwóch epokach: I epoka i, j; II epoka k, l
Definicja potrójnych różnic obserwacji fazowych:
![]()
![]()
Potrójne różnice = różnice podwójnych różnic dla dwóch epok
Równania potrójnych różnic:
![]()
![]()
![]()
gdzie
Informacje geodezyjne w wyrazie ![]()
, wyeliminowany wyraz ![]()
Potrójne różnice eliminują wpływ błędów
- zegarów satelitów
- zegarów odbiorników
- nieoznaczoności fazy
24. Porównanie pomiarów GPS kodowych i fazowych. Zastosowanie obu rodzajów pomiarów.
Code (pseudo - range) |
Phase |
|
Jest to zagadnienie na tyle obszerne, że można tu wykorzystać informacje z innych pytań głównie 20.
25. Problem inicjalizacji w pomiarach GPS. Rodzaje i sposoby inicjalizacji.
I odbiornika GPS to wyznaczenie nieoznaczoności fazy N, czyli znalezienie całkowitej liczby odłożeń fali w danej odległości. Znamy dzisiaj dwie grupy metod inicjalizacji - metody statyczne i kinematyczne. Najpopularniejsza obecnie jest metoda kinematyczna on - the - fly (patrz następne pytanie).
Istnieją również, niestosowane obecnie metody statyczne.
Metod statycznych już się nie stosuje, inicjalizacja za ich pomocą w technologiach kinematycznych jest czynnością dość uciążliwą.
26. Zasada inicjalizacji OTF. Wykaż na czym polega korzyść z jej stosowania.
OTF (on - the - fly) jest to obecnie najpopularniejsza metoda kinematyczna. Jest to sposób oparty na jednoczesnym wykorzystaniu pomiarów kodowych i fazowych. Wyznaczenie nieoznaczoności fazy N realizuje się na podstawie znanego wzoru:
![]()
Ze wzoru tego wyznacza się N mają pomierzoną wartość d z pomiaru kodowego. Problemem jest tu dokładność pomiaru d. Żeby wyznaczanie N miało sens, trzeba by ją był znać z dokładnością połowy długości hali czyli około 10cm, a jak wiadomą metoda kodowa takiej dokładności nie zapewnia. Dlatego do wyznaczenia N stosuje się kombinacje liniowe i sposoby iteracyjne.
27. Najważniejsze źródła błędów pomiarów GPS.
Technika pomiarów GPS jest techniką bardzo skomplikowaną a wysoka jej dokładność zależna od wielu czynników wymaga zastosowania i uwzględnienia specjalnych procedur obserwacyjnych i opracowania wyników obserwacji. Różnie można dzielić błędy wpływające na ostateczną dokładność wyników pomiarów GPS. Najlogiczniejszy jest podział na grupy:
Błędy systemu GPS
Błędy ośrodka i propagacji sygnału GPS
Błędy aparaturowe
Błędy wynikające z niewłaściwej geometrii konstelacji satelitów GPS
Błędy stosowanych technologii
Wpływ poszczególnych rodzajów błędów na pomiar GPS
Źródło błędu |
Błąd |
Błędy systemu błędy orbity błędy zegara |
1 - 2 m 1 - 2 m |
Wpływ ośrodka wpływ jonosfery (2 częstotliwości) model jonosfery („dobry”) model jonosfery („średnio dobry”) model jonosfery („niezbyt dobry”) wpływ troposfery (model) wielodrożność |
cm - dm 1 - 2 m 5 - 10 m 10 - 50 m dm 1 - 2 m |
Wpływy instrumentalne szum odbiornika opóźnienie w odbiorniku błąd centrum fazowego anteny |
0.2 - 1 m dm - m mm - cm |
28. Wymień czynniki, od których zależy dokładność pomiarów GPS.
Na dokładność wyznaczania pozycji mają wpływ
Osiągana dokładność (standardowa) pomiarów geodezyjnych GPS wynosi 10-6 (1mm na 1km). Możliwa do osiągnięcia dokładność pomiarów geodezyjnych GPS (przy zachowaniu specjalnych procedur pomiarowych i opracowania wyników) wynosi 10-7 - 10-8.
29. Pomiary bezwzględne i różnicowe. Dokładności.
Metoda (absolutna) bezwzględna. Mając do dyspozycji jeden tylko odbiornik satelitarny GPS można wyznaczyć współrzędne stanowiska anteny w układzie w którym podawane są orbity satelitów GPS (układ geocentryczny WGS 84 - World Geodetic System) odniesione do początku układu, tj. do środka ciężkości Ziemi. Jest to sposób najmniej dokładny i stosunkowo rzadko stosowany. Dokładność wyznaczania współrzędnych tym sposobem wynosi co najwyżej kilka metrów (metody klasyczne, naziemne zapewniały dokładność kilkaset metrów.
Metoda względna Stosuję się ją znacznie częściej niż metodę absolutną. W tym przypadku trzeba mieć co najmniej dwa odbiorniki GPS. W metodach względnych nie wyznaczamy współrzędnych X, Y, Z stanowisk, lecz różnice współrzędnych ΔX, ΔY, ΔZ pomiędzy wszystkimi punktami satelitarnymi uczestniczącymi w pomiarze. Dokładność tych metod jest znacznie wyższa, głównie ze względu na fakt, że wiele błędów, którymi obarczone są pomiary satelitarne (błędy szczątkowej refrakcji jonosferycznej i troposferycznej, błędy orbit satelitarnych, szczątkowe błędy niesynchronizacji zegarów itp.) w wyznaczeniu różnic eliminują się.
W skrócie:
Wyznaczanie położenia punktu pojedynczego (single point positioning)
Wyznaczanie względnego położenia punktów (relative positioning)
30. Dlaczego pomiary wykonywane w dłuższym okresie czasu są dokładniejsze.
W instrumentach ( odbiornik GPS ) można ustawić zliczenie obserwacji co pewien okres czasu . Przy dłuższym czasie obserwacji można uzyskać większą ilość tych zliczeń . Ponadto w dłuższym czasie zmienia się konstelacja satelitów - jest więcej obserwacji( do postprocessingu).
31. Jak usuwamy wpływ refrakcji jonosferycznej, a jak wpływ refrakcji troposferycznej.
Refrakcje jonosferyczną eliminuje się poprzez pomiar na dwóch odpowiednio dobranych częstotliwościach, i tworzeniu kombinacji liniowych wyników (dla pomiarów GPS będą to wyniki wzięte w stosunku 9:7)
Wpływ refrakcji troposferycznej usuwamy poprzez wprowadzenie poprawki, którą oblicza odbiornik automatycznie na podstawie wprowadzonego do jego wewnętrznego oprogramowania modelu atmosfery. Najprostszy model atmosfery (stacjonarny, tj. nie uwzględniający zmian parametrów atmosfery w czasie) stanowi zespół trzech wzorów wyrażających zmianę podstawowych parametrów atmosfery, tj temperatury, ciśnienia i gęstości w funkcji wysokości.
Atmosfera dzieli się na: jonosferę - znajdującą się na wysokości kilkudziesięciu kilometrów (60-80 km) zjonizowaną część atmosfery, troposferę, która z kolei dzieli się na wyższą - suchą w której nie ma pary wodnej i niższą - mokrą, znajdującą się na wysokości do 12 kilometrów.
Refrakcję, która występuje przy przechodzeniu przez jonosferę eliminuje się poprzez pomiar na dwóch częstotliwościach, które są tak dobrane, by średnia wartość z pomiaru na nich była wolna od jej wpływu. Np. TRANSIT (Doppler( wykorzystuje sygnały 180MHz i 400MHz. Stosuje się też inne podejście, polegające na tym że wpływu refrakcji pozbawiona jest pewna kombinacja liniowa (a nie średnia) pomiaru na dwóch częstotliwościach. Charakter refrakcji przy przechodzeniu przez jonosferę jest inny niż w przypadku troposfery.
Inaczej przedstawia się sytuacja w przypadku eliminacji refrakcji wynikającej z przejścia przez troposferę. Zarówno w przypadku techniki dopplerowskiej jak i GPS, w komputer wbudowany jest model atmosfery. Na tej podstawie komputer oblicza poprawkę i automatycznie uwzględnia w wyniku. Atmosferę charakteryzują zmiany temperatury ciśnienia i gęstości wraz z wysokością. Te trzy wzięte razem dają model (także na podstawie pomiarów empirycznych). Model taki może być różny od rzeczywistego, dlatego stosuje się pomiary translokacyjne. Jako że i tu i tu jest błąd, z różnicy się eliminuje, o ile oczywiście w obydwu punktach są takie same warunki. Stąd wynika warunek by przy pomiarach różnicowych odległości między stacjami nie były zbyt wielkie. Np. w jeśli w technice GPS chce się osiągnąć dokładności milimetrowe, odległość ta nie powinna przekraczać 12-15 km.
32. Jaki wpływ na dokładność pomiarów GPS ma konfiguracja geometryczna konstelacji satelitów GPS? Jak ocenia się jakość aktualnej konfiguracji satelitów GPS?

Wyznaczenie położenia z obserwacji GPS opiera się - z geometrycznego punktu widzenia - na procedurze trysferacji i jest geodezyjnym liniowym przestrzennym wcięciem wstecz. Dokładność wyznaczenia współrzędnych za pomocą wcięcia zależy od rozmieszczenia punktów o znanych współrzędnych wykorzystywanych w tej procedurze. W przypadku pomiarów GPS tworzone są przestrzenne konstrukcje - ostrosłupy, których wierzchołkiem jest wyznaczany punkt. Jest rzeczą oczywistą, że ze względów dokładnościowych korzystniejszy będzie przypadek, gdy satelity rozłożone będą po różnych stronach nieboskłonu; wówczas kąty przecięcia linii wyznaczających położenie punktu (stanowiska anteny GPS) nie będą zbyt ostre. Rysunek ilustruje dwa przypadki: dobrego i niekorzystnego rozmieszczenia satelitów wyznaczających położenie stanowiska.
W pomiarach GPS jakość geometrycznej konstelacji satelitów charakteryzuje tzw. współczynnik „Dilution of Precision” (DOP). Wartość współczynników DOP można policzyć na podstawie macierzy współczynników układu równań obserwacyjnych. W użyciu są różne rodzaje współczynników DOP:
HDOP - dla wyznaczenia współrzędnych horyzontalnych
VDOP - dla wyznaczenia współrzędnej pionowej
PDOP - dla wyznaczenia współrzędnych przestrzennych (3D)
TDOP - dla wyznaczenia czasu
Ciekawą interpretację geometryczną ma współczynnik do wyznaczeń przestrzennych PDOP. Jest on równy odwrotności objętości ostrosłupa utworzonego przez wyznaczone stanowisko i cztery satelity wykorzystywane do obliczeń. Im korzystniejsza jest konfiguracja geometrii satelitów, tym objętość ostrosłupa powinna być większa, czyli współczynnik PDOP - mniejszy. Współczynnik PDOP charakteryzujący w danej chwili geometrię konstelacji satelitów można odczytać z odbiornika satelitarnego GPS.
Przyjmuje się, że jeżeli współczynnik DOP jest zawarty między 1 i 3, to warunki do obserwacji SA bardzo dobre (Very Good), gdy wynosi 4 - 5, warunki można uznać za dobre (Good), gdy wynosi 6 - warunki należy ocenić jako słabe (ale dostateczne)(Fair), natomiast przy współczynniku DOP większym niż 6 nie należy wykonywać obserwacji. W naszych szerokościach DOP jest dobry i bardzo dobry (1-4).
33. Opracowanie „postprocessing” i pomiary w czasie rzeczywistym (real time kinematic RTK).
Postprocessing - dane obserwacyjne mogą być zbierane z wielu sesji w dłuższym okresie czasu. Opracowanie pomiarów następuje w biurze po zakończeniu prac polowych. Wynikiem opracowania są zazwyczaj współrzędne punktów mierzonej sieci. Wykorzystywana w technologiach statycznych.
Real time kinematic - (wynik w czasie rzeczywistym) pozycja jest wyznaczana na podstawie obserwacji w jednym momencie. Sposób stosowany w technologiach kinematycznych (nawigacyjnych). Pozycja obiektu ruchomego jest znana natychmiast w terenie. Istnieje możliwość postprocessingu dla tych obserwacji. Jest podstawą systemów nawigacyjnych wykorzystywanych przez użytkowników na lądzie morzu i w powietrzu. Możliwe wyznaczenie toru (trajektorii) obiektu ruchomego
34. Wytłumacz, dlaczego dokładność pomiarów GPS zależy od odległości między punktami wyznaczanymi.
Podstawową współczesną metodą pomiarów GPS, są pomiary względne. Oznacza to że wykorzystuje się dwa lub więcej odbiorniki, które wyznaczają swoje położenie względem siebie. Podstawowym czynnikiem rzutującym na dokładność pomiarów GPS jest wpływ atmosfery. Wprowadzono wprawdzie sposoby aby ten wpływ wyeliminować, ale nadal on istniej. Poprawka troposferyczna jest liczona na podstawie jakiegoś modelu atmosfery. Jeśli założymy w na danym obszarze atmosfera w takim samym stopniu zniekształca pomiar, to nawet gdy poprawka troposferyczna będzie wyznaczona niezbyt dokładnie, nie zaszkodzi to pomiarom względnym. Dzieje się to dlatego, ponieważ błąd ten dotyka w jednakowym pomiary na wszystkich stanowiskach, a więc różnic jest od niego wolna. Wszystko działa poprawnie o ile na stanowiskach panują takie same warunki atmosferyczne. Im stanowiska są bliżej siebie, tym warunki są bardziej zbliżone, im dalej, tym są one bardziej zróżnicowane, co rzutuje na dokładność.
35. Technologie pomiarów satelitarnych GPS (klasyfikacja, charakterystyka).
Zaliczamy do nich technologie:
Patrz również kolejne pytania.
36. Pomiary statyczne. Charakterystyka, dokładności, zalety, zastosowania.
Technologia pomiarów statycznych GPS jest technologią najwyższej dokładności. Oba odbiorniki uczestniczące w pomiarze pozostają stacjonarne w ciągu całej sesji (kampanii) obserwacyjnej. Możliwe jest zbieranie obserwacji z wielu sesji obserwacyjnych (np. po kilka godzin dziennie), zaś zebrany materiał jest poddawany opracowaniu po zakończeniu całej kampanii obserwacyjnej (tzw. „postprocesing”). Długość sesji (kampanii) obserwacyjnej zależy głównie od żądanej dokładności (przeznaczenia sieci). Np. dla sieci III klasy powinna ona wynosić około 80 - 90 minut. 1- 2 dni dla punktów odniesienia sieci krajowych i geodynamicznych o charakterze lokalnym i państwowym. 4-6 dni dla sieci kontynentalnych i podstawowych sieci geodynamicznych regionalnych. Przeznaczenie do wyznaczanie pozycji o najwyższej dokładności (1 - 2 mm). Stosuje się do pomiaru sieci geodezyjnych.
37. Pomiary kinematyczne. Charakterystyka, dokładności, zalety.
Technologia ta jest typową technologią nawigacyjną. W pomiarze bierze udział jeden odbiornik stacjonarny, względem którego wyznaczana jest pozycja drugiego ruchomego odbiornika umieszczonego na obiekcie poruszającym się. Możliwe jest otrzymywanie pozycji obiektu ruchomego w czasie rzeczywistym (natychmiastowe, np. co 1 sekundę, co 5 sekund; będzie to tzw. „Real time positioning”) albo też cały zebrany materiał obserwacyjny może być poddany opracowaniu po zakończeniu pomiarów („postprocessing”) w wyniku którego otrzymujemy obraz trasy, jaką przebył ruchomy obiekt. Podczas całej sesji obserwacyjnej niezbędna jest ciągła łączność z obserwowanymi satelitami. Stosuje się tu pomiary metodą fazową z inicjalizacja OTF. Metody statyczne w zastosowaniach nawigacyjnych nie sprawdzają się. Dokładność: 10 cm - 3 cm.
38. Pomiary pół - kinematyczne ( znane pod nazwą Stop and Go ). Charakterystyka, dokładności, zalety.
Wysiłki konstruktorów odbiorników i geodetów szły w kierunku skrócenia czasu pomiaru GPS w terenie i stworzenia technologii wyznaczenia położenia punktów, która nie wymagałaby wykonywania długotrwałych obserwacji statycznych. Pierwszą taka technologią był technologia znana pod nazwą „stop and go”, co można by przetłumaczyć jako „ zatrzymaj się i idź dalej”. Technologia ta będąca kombinacją technologii statycznych i kinematycznych wydawała się w pewnym okresie czasu bardzo atrakcyjna, jednak jej wady spowodowały, że w dalszym ciągu poszukiwano lepszych rozwiązań technologicznych. W pomiarze technologią „stop and go” biorą udział przynajmniej dwa odbiorniki, jeden umieszczony na punkcie odniesienia, drugi przemieszczający się z punktu na punkt. Niezbędna jest inicjalizacja statyczna na początku pomiaru. Niewątpliwą zaleta tej technologii jest to, że odbiornik ruchomy wykonuje pomiary na kolejnych punktach sieci tylko przez 1-2 minuty. Jednak w ciągu całej sesji pomiarowej (w czasie pomiarów na punktach i nawet w czasie transportu instrumentu z punktu na punkt) niezbędna jest nieprzerwana łączność z przynajmniej 4 satelitami GPS. Jest to podstawowa wada tej technologii uniemożliwiająca jej zastosowanie w terenie o wysokiej zabudowie, w lesie itd. Przejazd pod drzewami, pod wiaduktem lub mostem przerywa pomiar. Technologię tę można zatem stosować tylko w otwartym, nie porośniętym i niezabudowanym terenie. Dokładność ok. : 1-3 cm.
39. Pomiary pseudo - kinematyczne ( pseudo - statyczne ). Ponowne stawianie na punkcie („reoccupation”).
Następną technologią usuwającą podstawową wadę technologii „stop and go” jest technologia pseudo-statyczna (pseudo-kinematyczna) polegająca na dwukrotnym pomiarze GPS na każdym wyznaczonym punkcie, lecz niewymagająca ciągłej nieprzerwanej łączności z satelitami podczas transportu odbiornika z punktu na punkt. W pomiarze biorą udział przynajmniej dwa odbiorniki; jeden ustawiony na punkcie odniesienia, drugi przemieszczający się z punktu na punkt. Pomiar na każdym punkcie trwa około 10-15 minut, wykonujemy pomiary na kolejnych punktach sieci, na ostatnim wyznaczanym punkcie czekamy (drugie śniadanie) 1-2 godziny na zmianę konfiguracji satelitów i ponownie wykonujemy pomiar GPS na punktach wyznaczanych (reoccupation). Ten podwójny pomiar GPS na każdym stanowisku przy różnych konfiguracjach satelitów zastępuje proces inicjalizacji. Zaletą tej technologii jest to, że nie jest wymagana łączność z satelitami podczas transportu odbiornika z punktu na punkt, wadą natomiast konieczność dwukrotnego stawania na tym samym punkcie. Dokładność ok. 1cm.
40. Pomiary szybkie statyczne. Charakterystyka, dokładności, zalety (FAST/RAPID STATIC).
W pomiarze biorą udział, podobnie jak poprzednio, przynajmniej dwa odbiorniki GPS, jeden ustawiony na punkcie odniesienia, drugi przemieszczający się z punktu na punkt. Technologia wymaga jednokrotnego pomiaru na każdym wyznaczanym punkcie, nie wymaga nieprzerwanej ciągłości śledzenia satelitów w czasie transportu odbiornika z punktu na punkt, jednak pomiar tą technologią można wykonać jedynie odbiornikami dwuczęstotliwościowymi (z kodem P) z wbudowanym specjalnym oprogramowaniem wewnętrznym. Czas obserwacji na stanowisku zależy od liczby obserwowanych satelitów (pożądane 5 -6) i wynosi około 20 minut przy obserwacji 4 satelitów, 15 minut przy obserwacji 5 satelitów i około 8 minut przy obserwacji 6 satelitów. Istotą pomiaru jest szybkie wyznaczanie nieoznaczoności fazy przy wykorzystaniu kombinacji pomiarów kodowych i fazowych na obu częstotliwościach L1 i L2. Technologia ta należy do najczęściej używanych. Dokładność ok. 1cm.
41. Jakie odbiorniki satelitarne GPS mogą być zastosowane do pomiaru technologią „fast static”? Od czego zależy czas trwania obserwacji na stanowisku?
Pomiar tą technologią można wykonać jedynie odbiornikami dwuczęstotliwościowymi (z kodem P) z wbudowanym specjalnym oprogramowaniem wewnętrznym. Czas obserwacji na stanowisku zależy od liczby obserwowanych satelitów (pożądane 5 -6) i wynosi około 20 minut przy obserwacji 4 satelitów, 15 minut przy obserwacji 5 satelitów i około 8 minut przy obserwacji 6 satelitów.
42. Kolejność czynności wykonywanych przez obserwatora na stanowisku podczas pomiaru technologią Fast static.
wprowadzamy “elevation mask” - 15stopni i inne np. min czas obserw.?
START - wówczas rozpoczyna się obserwacja
- zakończenie całego cyklu obserwacji - opcja- END SURVEY
43. Pomiary DGPS . Zasada, charakterystyka, dokładności, zalety, zastosowania.
Pomiary dyferencyjne są szczególnym przypadkiem pomiarów względnych GPS. Technologia DGPS opiera się w zasadzie na pomiarach nawigacyjnych kodowych (pseudoodległości) wykonywanych w czasie rzeczywistym, jednak w ostatnim czasie w technologiach tych stosowane są już pomiary fazowe i opracowanie typu „postprocessing”. Technologia DGPS wykorzystuje oczywistą zasadę mówiącą, że wpływ błędów ośrodka (głównie troposfery i jonosfery) w danej chwili na pomiary na stacji bazowej i na punkcie wyznaczanym położonym niezbyt daleko od stacji bazowej są takie same. Stacja bazowa jest umieszczona na punkcie o znanych współrzędnych. Podczas pomiaru wyznacza ona swoje współrzędne, zaś różnice między znanymi współrzędnymi stacji bazowej i wyznaczonymi z poszczególnych pomiarów (np. co sekundę) traktowane są jako poprawki korekcyjne, o które należy poprawić również wyznaczenia współrzędnych na punkcie ruchomych. Dla obliczenia poprawek korekcyjnych stosuje się w pewnym etapie rachunek różniczkowy (stąd nazwa „differentia” GPS); stosowane dzisiaj poprawki korekcyjne dotyczą albo poprawiania wprost wyznaczanych współrzędnych punktu ruchomego, albo poprawiania pomierzonych odległości do satelitów, na podstawie których wyznaczane jest położenie punktu ruchomego. Istotą technologii DGPS jest również i to, że stacja bazowa transmituje do odbiornika ruchomego poprawki, które są na bieżąco wykorzystywane przez odbiornik ruchomy do obliczania poprawionej pozycji anteny odbiornika ruchomego. Transmisja może się odbywać przy wykorzystaniu różnych środków przekazu: stacji radiowej UKF, telefonii komórkowej, Internetu itd. Dokładność pomiarów DGPS opartych tylko na pomiarach kodowych wynosi 1-2 m. jest to dokładność zupełnie wystarczająca dla celów nawigacyjnych, np. wyznaczania (ustalania) pozycji radiowozów policyjnych, ambulansów pogotowia ratunkowego, pojazdów straży pożarnej, pociągów, środków transportu samochodowego itd. Zastosowanie pomiarów fazowych pozwala wyznaczyć współrzędne z dokładnością centymetrową. Na tej zasadzie pracują dzisiaj różne krajowe i krajowe systemy nawigacyjne morskie i lotnicze.
44. Uzasadnij potrzebę tworzenia krajowych systemów nawigacyjnych.
45. Programy (firmowe) opracowania pomiarów GPS.
Programy firmowe do redukcji obserwacji:
Programy do redukcji obserwacji prac geodezyjnych o charakterze naukowym (zakładanie jednolitych podstawowych osnów geodezyjnych o zasięgu kontynentalnym EUREF, a także zagęszczanie tych osnów na obszarze poszczególnych krajów):
BERNES , DIPOP , GAMIT , GEONAP , GIPSY , TOPAS.
Programy te służą do przygotowania planu obserwacji, przygotowania instrumentu, obliczenia pomierzonych cięciw, wyrównania pomierzonej sieci, transformacje, analiza sieci (dokładnościowa).
46. Zalety pomiarów GPS.
47. Wady pomiarów GPS.
- selective availability ( SA ), (ograniczenie dokładności poprawki zegara pokładowego i elementów pozycji satelity),
- anti-spoofing (AS ), (zastąpienie kodu P tajnym kodem Y),
48. Zastosowania pomiarów GPS.
49. Problem wyznaczania wysokości za pomocą pomiarów GPS („GPS levelling”).
Jako wyników pomiarów GPS otrzymujemy prostokątne współrzędne X, Y, Z pozycji anten odbiorników. Współrzędne te można łatwo przeliczyć na współrzędne geodezyjne B, L, H odniesione do układu współrzędnych WGS 84. Nas zazwyczaj interesują jednak wysokości odniesione do geoidy (poziomu morza), zatem aby obliczyć wysokość punktu h liczoną od poziomu morza (wysokość ortometryczną), należy od wysokości elipsoidalnej punktu H odjąć wysokość geoidy N, czyli
h = H - N
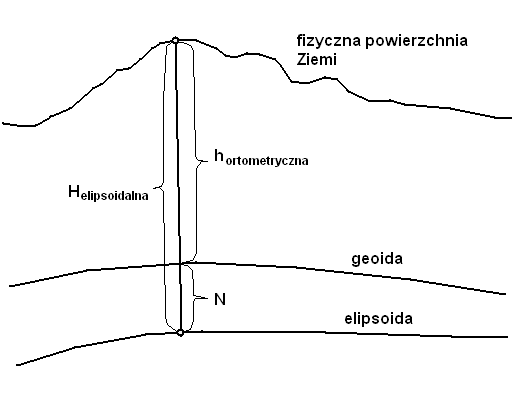
Rysunek przedstawia problem wyznaczania wysokości ortometrycznej punktu na podstawie pomiarów GPS w sposób uproszczony, zaniedbujemy bowiem tu fakt, że wysokość ortometryczną liczymy wzdłuż zakrzywionej linii pionu oraz utożsamiamy powierzchnię morza z powierzchnią geoidy, co nie jest w pełni spełnione.
Aby wyznaczyć wysokość punktów nad poziom morza (ortometryczną) należy więc znać wysokość geoidy (odległości - odstępy geoidy od elipsoidy) w miejscach, gdzie wykonywaliśmy pomiar GPS.
50. Wyznaczenie wysokości geoidy za pomocą pomiarów GPS.
Potrzebne wysokości geoidy N możemy wziąć albo z mapy wysokości geoidy (centymetrowej),o ile dla terenu, gdzie prowadzimy pomiar takie mapy istnieją, albo możemy wysokość N obliczyć znanymi z geodezji klasycznej metodami - na podstawie znanych anomalii grawimetrycznych ze wzoru Stokes'a, lub za pomocą niwelacji astronomicznej lub astronomiczno - grawimetrycznej. Musimy sobie jednak zdawać sprawę, że dokładność tych wyznaczeń wysokości N jest znacznie gorsza (kilkadziesiąt centymetrów) niż dokładność wysokości elipsoidalnych h wyznaczonych z pomiarów GPS. Dokładniejszym sposobem byłoby wyznaczenie wysokości geoidy N z pomiarów satelitarnych GPS i wyników niwelacji precyzyjnej. Jeśli wykonalibyśmy pomiar GPS na kilku reperach niwelacji precyzyjnej, dla których wysokość h nad poziomem morza są znane, to wysokości geoidy obliczylibyśmy ze wzoru:
N = H - h
Sposobem tym możemy wyznaczyć wysokość geoidy z możliwie najwyższą dzisiaj do osiągnięcia dokładnością (milimetry - kilka centymetrów). Dla pozostałych punktów położonych wewnątrz obszaru wartości wysokości geoidy można wyznaczyć poprzez interpolację. Jednak sposób ten jest możliwy do zastosowania jedynie w terenach, gdzie zmiany wysokości geoidy są niewielkie i mają charakter regularny i liniowy.
Najczęściej chodzi nam o wyznaczenie nie samych wysokości punktów, a różnicy wysokości, czyli
Δh = ΔH - ΔN
Podobnie mamy
ΔN = ΔH - Δh
Niezbędne do realizacji tych wzorów różnice wysokości geoidy obarczone są mniejszymi błędami, przeto różnice wysokości są wyznaczane z nieco większą dokładnością.
Mniejsze dokładności użytych do obliczeń wysokości geoidy N niż samych pomiarów satelitarnych GPS wysokości elipsoidalnych (H) powodują, że dokładności niwelacji satelitarnej można porównać z dokładnością raczej klasycznej niwelacji technicznej niż niwelacji precyzyjnej. Stąd nadal proponuje się, aby stosunkowo krótkie linie (do kilkudziesięciu kilometrów) mierzyć za pomocą tradycyjnej klasycznej niwelacji precyzyjnej. Niwelacja satelitarna staje się bardziej ekonomiczna i uzasadniona ze względów dokładnościowych przy wyznaczaniu różnic wysokości między bardziej odległymi punktami (stu i więcej kilometrów).
Więcej o wyznaczaniu N na podstawie pomiarów GPS i pomiarów astronomicznych lub niwelacji trygonometrycznej w książce Czarneckiego.
51. Uzasadnij dlaczego technika GPS spowodowała rewolucję technologiczna w geodezji.
52. Ogólna charakterystyka strategii wykonywania obserwacji GPS w sieciach geodezyjnych.
Trzy podstawowe strategie obserwacji
53. Metoda „gwiazdowa” i „zamkniętych figur” w strategiach obserwacji GPS. Wady i zalety.
- punkt centralny „gwiazdy” mierzy się w oddzielnych sesjach pomiarowych (dokładnie metodą statyczną)
- pozostałe punkty wyznacza się względem punktów centralnych
- pożądane sesje kontrolne pomiędzy punktami nie mierzonymi we wspólnych sesjach
- metoda daje bardzo dokładny wynik, lecz jest bardzo pracochłonna
- niektóre punkty tworzonej sieci mierzone są przynajmniej w dwóch seriach obserwacyjnych
54. Różne aspekty ustalania planu obserwacji. Podstawowe zasady tworzenia sieci GPS.
Trzy podstawowe zasady tworzenia sieci satelitarnych GPS
- długość sesji obserwacyjnych
- wykorzystanie odpowiednich technologii
- korzystne konstelacje geometryczne (DOP)
- liczba odbiorników użytych w kampanii
- ustalenie odpowiedniej liczby sesji
- ustalenie najkorzystniejszych przemieszczeń odbiorników
- zminimalizowanie drogi i czasu transportu
- udział niektórych wybranych punktów sieci w kilku sesjach obserwacyjnych przy różnych konstelacjach satelitów
- pomiar cięciw kontrolnych
- dowiązanie do punktów kontrolnych
Przygotowanie pomiaru sieci satelitarnej
W celu dobrego przygotowania należy sobie odpowiedzieć na pytania:
55. Jakie korzyści przynosi nawiązanie sieci lokalnej di tzw. „punktach permanentnych”?
56. Rola punktów permanentnych GPS w geodezji i badaniach geodynamicznych.
Stacje na punktach permanentnych służą do monitorowania europejskiego układu odniesienia EUREF. Na stacjach tych utrzymywane są również inne służby permanentne takie jak wykonujące pomiary laserowe do satelitów (SLR), grawimetryczna służba pływowa, służba czasu, pomiary astronomiczne, meteorologiczne, służba stanu jonosfery. Stacje te wykorzystuje się jako stacje DGPS, a więc mające znaczenie w nawigacji.
57. Podstawowe satelitarne sieci geodezyjne na terenie Polski.
EUREF-POL
W sumie istnieje ok. 1000 punktów.
IGS
SAGET
EXTENDED SAGET
europejska sieć geodynamiczna, rozszerzona o Polskę
CERGOP
Na terenie Polski są również sieci geodynamiczne: najdłuższa linia geodynamiczna pomierzona w Polsce - to LAMKÓWKO- BOROWA GÓRA - JÓZEFOSŁAW - ŚWIĘTY KRZYŻ - GRYBÓW - PIENINY.
58. Kampania EUREF-POL i jej szczególne znaczenie.
EUREF to europejski układ odniesienia. W 1992 roku rozszerzył się na terytorium Polski. Pomierzono 11 punktów, które były punktami odniesienia Krajowej Sieci Dopplerowskiej, bądź obserwatoriami astronomiczno - geodezyjnymi (Grybów, Józefosław, Borowiec, Lamkówko, Borowa Góra, Zubowice, Rogaczew, Studnice, Czarnkowo, Masze, Rozewie). Stworzono dzięki temu warunki do powiązania istniejącej sieci astro.- geodezyjnej z układem EUREF`89.
Punkty Kampanii EUREF-POL posłużyły do zagęszczenia osnowy do boków o długości 30-50km, dając możliwość wykonywania różnych metod pomiarów.
Punkty polskiej części sieci zostały tak dobrane, że została stworzona możliwość powiązania istniejącej sieci astronomiczno-geodezyjnej z układem EUREF i wykorzystana z wcześniejszych prac z zakresu geodezji satelitarnej. Została stworzona podstawa do zapewnienia ciągłości prac badawczych w zakresie geodynamiki w Polsce. Wykonując pomiary geodezyjne, głównie techniką GPS, ale również geodezyjnymi technikami naziemnymi i dowiązując te pomiary do punktów EUREF, przenosimy europejski układ współrzędnych na obszar objęty pomiarami. Następnie można dokonywać transformacji do dotychczas stosowanego układu odniesienia.
Punkty Kampanii EUREF-POL posłużyły do zagęszczenia osnowy do boków o długości 30-50km, dając możliwość wykonywania różnych metod pomiarów. Stacje Euref - Pol służą do monitorowania stabilności układu europejskiego. EUREF - POL włączył Polskę do sieci europejskiej.
59. Sieć satelitarna założona na terenie Polski przy udziale amerykańskiej agencji DMA.
W roku 1993 geodezyjna służba wojskowa zawarła porozumienie z amerykańska instytucją geodezyjną Defense Mapping Agency (DMA), wynikiem której było zagęszczenie sieci EUREF-POL. Ekipy trzech instytucji DMA, polskiej wojskowej służby geodezyjnej oraz Instytutu Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej pomierzyły 45 punktów sieci podstawowej GPS.
60. Podstawowa satelitarna sieć wojskowa.
W latach 1994 - 1996 ekipy wojskowej i cywilnej służby geodezyjnej w Polsce zakładały równolegle satelitarną „sieć wojskową” i „sieć cywilną”. Filozofia zakładania sieci wojskowej była inna filozofii zakładania sieci cywilnej. Sieć wojskowa (około 550 punktów) powstawała ściśle według reguł zakładania nowoczesnych sieci satelitarnych GPS (lokalizacja punktów przy traktach komunikacyjnych) i jest dostosowana do dowiązania pomiarów wykonywanych szybkimi technologiami naziemnymi stosowanymi w wojsku.
61. Sieć cywilna POLREF.
Sieć cywilna POLREF (około 350 punktów) uwzględnia w większym stopniu punkty klasycznej sieci astronomiczno - geodezyjnej istniejącej na trenie Polski.
62. System GLONASS. Zasada systemu, układ satelitów GLONASS, charakterystyka sygnału.
- orbity prawie kołowe
- wysokość h = 19100 km
- okres obiegu T = 11,25 h
- nachylenie i = 64,8 °
![]()
dla k=1,2,…,24
![]()
Okres „świetności” system miał w latach osiemdziesiątych. Do niedawna, liczba satelitów ciągle malała (brak funduszy), tak że system przestał być operacyjny. Sytuacja zmieniła się gdy do władzy w Rosji doszedł Władimir Putin, który posiadanie własnego (niezależnego od Amerykańców) globalnego systemu wyznaczania pozycji uznał z priorytet i zarządził renowacje i unowocześnienie GLONASSa. Rosjanie zapowiadają że w 2007 po orbitach będzie krążyć 12 satelitów (dzisiaj jest to 8 sztuk). W latach 2006 - 2026 planują wystrzeliwanie na orbitę satelitów GLONASS - K, które charakteryzują się zwiększoną żywotnością (10 lat w porównaniu do obecnie stosowanych GLONASS M - 7 lat, czy już wycofywanych z orbit starszych modeli które latały sobie 3 lata i spadały, w najmniej odpowiednim czasie i miejscu). Razem z tymi satelitami ma wejść drugi i trzeci sygnał dla użytkowników cywilnych. Od 2015 ma być też używana nowa generacja satelitów. Póki co wiemy tylko że nazywa się GLONASS - KM.
63. Korzyści płynące z łącznego stosowania GPS i GLONASS.
Każdy z systemów docelowo ma mieć po około 30 satelitów. Jeśli systemy były by kompatybilne to w każdym momencie można by wykonywać pomiar wykorzystując 15 (włączając GALILEO) i więcej satelitów. Zwiększyło by to dokładność i szybkość pomiaru, a ponadto umożliwiło pomiary satelitarne w wysokiej zabudowie miast. Zwiększyło by to niezawodność i bezpieczeństwo. Systemy są niezależne, więc awaria jednego z nich w żaden sposób nie wpływa na pozostałe.
64. Trudności w łącznym stosowaniu GPS i GLONAS.
65. Jakie cechy musi mieć system satelitarny, aby mógł być on przyjęty jako system nawigacyjny?
66. Czy system GPS może być systemem nawigacyjnym w pełnym tego słowa znaczeniu?
Mimo że GPS bywa często nazywany GNSS (Global Navigation Satelite Systems), to NIE jest on systemem nawigacyjnym. System nawigacyjny musi spełniać oczekiwania nawigacji lądowej morskiej i lotniczej. Najbardziej wymagająca jest oczywiście nawigacja lotnicza, żądająca bardzo wysokich dokładności, nieprzerwanego działania w czasie rzeczywistym i pewności że otrzymywane sygnały satelitarne są poprawne. Ani GPS ani GLONASS nie spełniają tych warunków i wobec tego żaden z nich nie może być uznany za system nawigacyjny i stanowić główny system nawigacyjny, na którym można by było oprzeć nawigację lotniczą. Poniższa tabela zawiera wymagane dokładności (znacznie zgeneralizowane) dla różnych zastosowań nawigacji:
67. Sposoby augmentacji systemów satelitarnych.
System GPS sam w sobie nie jest więc systemem nawigacyjnym; trzeba go uzupełniać. Stosuje się liczne systemy wzmacniające, których głównym celem jest kontrola poprawności funkcjonowania systemu.
RAIM
DGPS (LADGPS, WADGPS)
SBAS (WAAS, EGNOS, C-WASS…)
GBAS, ABAS
RAIM - (receiver autonomous integrity monitoring). Algorytm programu RAIM wykorzystywany w odbiorniku użytkownika dla wykrycia złego funkcjonowania systemu satelitarnego. Wymaga obserwacji przynajmniej 5 satelitów (porównywanie różnych kombinacji wyznaczania położenia)
DGPS - jego zastosowanie zwiększa dokładność. Możliwe są jego dwa warianty:
LADGPS - (Local Area DGPS) z jedną stacja bazową
WADGPS - (Wide Area DGPS) z większą liczbą zespolonych stacji bazowych pod kontrolą Master Control Stadion
SBAS - (Satellite Based Augmentation System) - system ten zwiększa integrity monitoring, continuity of sernice, time availability, accuracy performance for landing. Obecnie funkcjonujące systemy wykorzystują satelity geostacjonarne i sieć naziemnych stacji referencyjnych.
WASS (Wide Area Augmentation System) - USA
EGNOS (European Geostationary Navigation System) - Europa
MSAT (Multi-functional Satellite-based Augmentation Sernice) - Japonia,
SNAS (satellite Navigation Augmentation System) - Chiny
C - WAAS (Canadian extension of US WAAS) - Kanada
GBAS (Ground Based Augmentation System) - obecnie używane systemy to :
LAAS (Local Area Augmentation System). LAAS składa się z stacji referencyjnych, stacji śledzących odbierających sygnał z satelity, stacji referencyjnych wysyłających sygnał do użytkownika, pseudolitów umieszczonych wzdłuż pasów startowych lotnisk .
ABAS (Aircraft Based Augmentation System) - system ten wykorzystuje sygnały satelitów GPS oraz innych systemów nawigacyjnych DME, VOR, LORAN-C, OMEGA, INS. Kontrola polega na porównaniu wyznaczenia położenia na podstawie systemu GPS i innych systemów.
Podstawowe elementy oceny systemu nawigacji (bonus)
68. Systemy WAAS i LAAS.
WASS (Wide Area Augmentation System) to amerykańska wersja SBAS (Satellite Based Augmentation System). Amerykański satelitarny system wspomagający system GPS. Za pośrednictwem dwóch satelitów geostacjonarnych obejmujących terytorium Stanów Zjednoczonych transmituje poprawki kompensujące błędy jonosfery, zegara i efemeryd. Na system składa się również 30 stacji naziemnych.
(ze strony internetowej)
System z założenia nie działa samodzielnie lecz jest uzupełnieniem systemu GPS. Pozwala na zmniejszenie błędu pomiaru pozycji z 10 m poniżej 3 metrów w odbiornikach przystosowanych do odbioru sygnału WAAS. Składa się z naziemnych stacji referencyjnych które przesyłają poprawki do dwóch satelitów geostacjonarnych EGNOS (AOR-E, IOR). W Polsce mamy już taką stację zlokalizowaną w Centrum Badań Kosmicznych PAN w Warszawie. Za pośrednictwem wspomnianych satelitów, sygnał trafia do odbiorników GPS pozwalając na skorygowanie pomiaru dokonanego na podstawie danych z satelitów GPS. EGNOS jest obecnie w fazie wdrażania, przeprowadzane są testy, dlatego dostępność sygnału jest okresowa, mimo że satelity WAAS mogą być stale widoczne na ekranie odbiornika.
System występuje w trzech kompatybilnych ze sobą wersjach regionalnych : WAAS w Ameryce, EGNOS w Europie oraz japoński MSAS w Azji. Mnogość nazw jest skutkiem zarządzania każdego z systemów przez odrębne instytucje. Jako że wersja w zasięgu której się znajdziemy nosi nazwę EGNOS, natomiast producent odbiorników np. Garmin znajduje się w zasięgu WAAS - w Polsce często używa się zamiennie obu tych nazw. WAAS, EGNOS i MSAS są też niekiedy wspólnie określane jako SBAS (Satellite-Based Augmentation Systems).
LAAS (Local Area Augmentation System). LAAS składa się z stacji referencyjnych, stacji śledzących odbierających sygnał z satelity, stacji referencyjnych wysyłających sygnał do użytkownika, pseudolitów umieszczonych wzdłuż pasów startowych lotnisk .
(ze strony internetowej)
Systemy o zasięgu lokalnym są określane jako LAAS (Local Area Augmentation System) albo LADGPS (Local Area Differential GPS). Projektuje się użycie LADGPS tam, gdzie WAAS nie sięga, albo w rejonach, w których trzeba lokalnie podnieść jego dokładność i niezawodność. Największe zalety systemów różnicowych o zasięgu lokalnym to:
69. System SAPOS.
SAPOS to niemiecki system pozycyjny. Budowany przez około 10 lat system stacji został na początku 2002 roku oddany do użytku. System SAPOS oferuje cztery zakresy serwisu charakteryzujące się różną dokładnością:
W systemie dział 257 stacji referencyjnych działających w sieci, zaś otrzymywane przez użytkownika poprawki korekcyjne podawane są jako poprawki systemu a nie poprawki wyznaczane przez poszczególne stacje. Powoduje to wydatne zwiększenie dokładności i zmniejszenie błędów zależnych od odległości wyznaczanego punktu od poszczególnych stacji referencyjnych. Na systemie niemieckim wzorowany jest system powstający w Polsce.
70. System SWEPOS.
SWEPOS to szwedzki system pozycyjny. Opiera się on na 25 stacjach referencyjnych emitujących poprawki korekcyjne DGPS. System jest wykorzystywany do wyznaczeń pozycji w czasie rzeczywistym (na znacznej części obszaru kraju) z metrową dokładnością obiektów ruchomych i zbierania danych dla systemów informacji przestrzennej o terenie, a także do wyznaczenia współrzędnych punktów sieci geodezyjnych i badania współczesnych ruchów skorupy ziemskiej milimetrową dokładnością.
71. System EGNOS.
W Europie działa już EGNOS (European Geostation Navigation Overly Service) na który składają się segmenty:
- GPS
- GLONASS
- INMARSAT-3, AOR - E
- INMARSAT IOR
- ESA ARTEMIS
Więcej, patrz pytanie 68.
72. System GALILEO.
GALILEO to globalny europejski system wyznaczania pozycji.
Dlaczego Europa chce mieć swój system?
Segmenty GALILEO:
Praca systemu GALILEO
Istnieją trzy możliwości:
Koszty
Całkowity koszt EGNOS to 3250 milionów €. Utrzymanie systemu EGNOS kosztuje 25 milionów € na rok, natomiast GALILEO 220 milionów € na rok. W celu finansowania przedsięwzięcia utworzono PPP (public private partnership), który będzie odpowiadał min. za pobieranie opłat za korzystanie z systemu.
Instytucje odpowiadające za GALILEO
Skutki wprowadzenia GALILEO
Kompatybilność systemu
26 czerwca 2004 roku podpisano umowę pomiędzy przedstawicielami systemów GPS, GALILEO w sprawie współpracy i kompatybilności systemów. Główne punkty tej umowy to:
standardy bezpieczeństwa nawigacji lotniczej morskiej
73. System EUPOS.
Jest to system wspomagający powstający na terenie EUROPY. Obecnie planuje się jego założenie w 15 krajach w tym W Polsce. Z inicjatywą utworzenie systemu wystąpił Departament Geodezji Senatu Berlina i udostępnił standardy systemu (nie trzeba ich wypracowywać na nowo). 4-5 marca 2002 roku powołano Komitet Sterujący w którym zasiadają przedstawiciele poszczególnych krajów w tym Śledziński. Komitet dyskutuje nad standardami, finansowaniem itp. EPOS będzie zawierał 900 permanentnie działających stacji (500 w Rosji) rozmieszczonych co 70 - 80 km. System puki co będzie opierał się na GPS, później na GALILEO. Wszystkie kraje będą zachowywać te same standardy.
Polska część ASG EUPOS (aktywna sieć geodezyjna) będzie się składać z 87 stowarzyszonych stacji (poprawki będą liczone przez wszystkie stacje). Centrum obliczeniowe będzie się wieścić w Józefosławiu.
74. Misje satelitarne.
Satelita CHAMP (CHAllenging Minisatellite Payload) realizuje misję satelitarną, której celem jest zbadanie Ziemi jako systemu globalnego składającego się z lądów, oceanów i atmosfery. Trzy główne cele tej misji to:
• wyznaczanie i badanie zmian pola grawitacyjnego Ziemi w czasie,
• badanie pola magnetycznego Ziemi i jego zmian w czasie,
• badanie atmosfery (głównie jonosfery) w celu wyznaczenia zmian klimatycznych oraz przewidywania pogody.
Na satelicie zostały umieszczone między innymi: antena systemu GPS, retroreflektory SLR, magnetometr i kamera CCD wykonująca zdjęcia gwiazd. Misja rozpoczęła się 15 czerwca 2000. Satelita został umieszczony na wysokości 450 km na orbicie prawie kołowej o nachyleniu 87°. Dzięki tej misji powstały już dwa modele pola grawitacyjnego Ziemi: EIGEN-1 i EIGEN-2, jak również stworzono mapę pola magnetycznego litosfery ziemskiej
DORIS - system składa się z odbiorników na satelitach i 50 transmisyjnych stacji naziemnych. Główny cel systemu to wyznaczanie precyzyjnych orbit satelitów. Poza ty wyznaczanie pozycji stacji transmisyjnych, badanie pola grawitacyjnego, badanie położenia środka Ziemi i inne. Zasada działania opiera się na efekcie doplera. Stacje naziemne wysyłają sygnał na dwóch częstotliwościach i na podstawie przesunięcia dopplerowskiego wyznaczana jest odległość (dokładność 0.3 - 0.5 mm/s). Odbiorników na satelitach - obecnie SPOT 2, SPOT 4, TOPEX, Envisat,
Jason i w przyszłości SPOT 5.
GOCE - misja ma na celu wyznaczenie geoidy światowej z dokładnością 1 cm, oraz otrzymanie anomalii grawimetrycznych. Istota badania polega na tym że po dwóch orbitach leżących w jednej płaszczyźnie („jedna nad drugą”) poruszają się z równą prędkością kątowo satelity. Satelita na niższej orbicie podlega wpływowi pola grawitacyjnego. Wpływy te bada satelita poruszający się po orbicie wyższej mierząc przesunięcia orbity niższej.
Misja GRACE (Gravity Recovery and Climate Experiment) to dwa satelity
odległe od siebie o 220 km. Obydwa satelity od 17 marca 2002 znajdują się na
orbicie bliskiej polarnej, o nachyleniu 89◦, na wysokości od 300 km do 500 km.
Głównym celem misji GRACE jest uzyskiwanie zarówno statycznego jak i zmiennego w czasie modelu pola grawitacyjnego Ziemi o bardzo dużej dokładności w okresach co 30 dni przez 5 lat. Stworzony zostanie również profil ciśnienia, temperatury i wilgotności dla atmosfery oraz wyznaczone zostaną zmienne opisujące jonosferę.
Kolejnym zadaniem misji jest globalne badanie klimatu i jego zmian. W tym celu zostaną przeprowadzone badania prądów oceanicznych i transportu ciepła w oceanach oraz zmiany masy oceanów i lodowców. To wszystko możliwe jest dzięki bardzo dokładnym pomiarom odległości między satelitami przy użyciu mikrofal. Oprócz tego każdy z satelitów został wyposażony w anteny systemu GPS, który zastosowano tu do wyznaczania dokładnej pozycji obu satelitów, jak również do wyznaczenia opóźnienia fal radiowych przy ich przejściu przez atmosferę.
Misja PRARE - zainicjowana przez University of Stuttgart. Oprócz typowych pomiarów wykonywał będzie badanie topografii i wysokości mórz i oceanów.
75. Najważniejsze międzynarodowe organizacje naukowe.
76. Najistotniejsze cykliczne sympozja i konferencje.
77. Program IGGOS.
Integrated Globar Geodetic Observing System
Zadania:
78. Sieci IGS, EPN, CERGOP, SAGET.
(część opisana w pytaniu 57)
32
3
![]()
Wyszukiwarka
Podobne podstrony:
GPS Vector data(2), gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, Kozowy folder
Pytania ze sprawdziaz satki, gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna
projekt sieci, gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, siec gps II klasy
wyrównanie wojtek, gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, Kozowy folder
operat 1satka, gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, sprawka
satka 2, gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, sprawka
satka stare egzaminy, gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, Geodezja Satelitarna
GPS Vector data(2), gik, semestr 4, satelitarna, Satka, Geodezja Satelitarna, Kozowy folder
sciaga 1 kolos, gik, semestr 4, satelitarna, Satka, Satelitarna
wykład2, gik, semestr 4, kartografia
wykład3, gik, semestr 4, kartografia
Wykład6, gik, semestr 4, kartografia
Wykład7, gik, semestr 4, kartografia
wyklady2, gik, semestr 3, etp
Porównanie pomiarów uzyskanych niwelatorem technicznym i laserowym, gik, semestr 5, GIP, GIP Geodezj
SUWNICA, gik, semestr 5, GIP, GIP Geodezja Inżynieryjno-Przemysłowa, kolos
jakieś zaliczenie wykladow, gik, semestr 5, GIP, wykłady 6 sem, fwdpdgip
więcej podobnych podstron