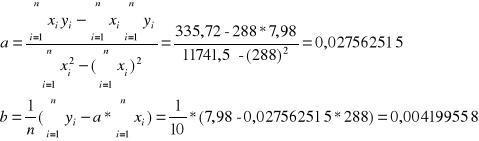Piotr Wiśniewski 25.X.2002
Ćwiczenie 43
Temat: Wyznaczanie współczynników temperaturowych rozszerzalności liniowej i oporu elektrycznego dla metali i stopów.
Tabela wyników:
Teoria:
Unoszenie - przykładem przenoszenia się ciepła wraz z materią - unoszenie ciepła - może być płomień zwykłego palnika gazowego. Powietrze znajdujące się w bezpośredniej bliskości płomienia po ogrzaniu posiada mniejszą gęstość, niż powietrze otaczające, dzięki temu wytwarza się prąd ogrzewanego powietrza ku górze, przenoszący ze sobą energię cieplną.
Promieniowanie - stosujemy tu twierdzenie:
Przewodnictwo
Obliczenia:
Niepewność pomiarowa:
Niepewność dla a :
niepewność dla
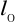
:niepewność dla
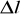
:niepewność dla T:
pochodna po
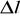
:pochodna po
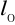
:pochodna po
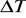
:niepewność całkowita:
niepewność rozszerzona:
wynik:
Niepewność dla
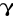
:niepewność dla
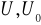
:niepewność dla
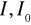
:niepewność dla T:
pochodna po U :
pochodna po
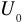
:pochodna po I :
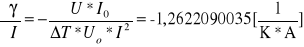
pochodna po
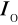
:pochodna po
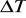
:niepewność całkowita:
niepewność rozszerzona:
wynik:
Wnioski:
Lp. |
U [V] |
E [mV] |
l [mm] |
T [K] |
I [A] |
R |
1 |
1 |
0,1 |
0,03 |
2,5 |
0,1513 |
6,609385327 |
2 |
2 |
0,3 |
0,13 |
7,5 |
0,325 |
6,153846154 |
3 |
3 |
0,5 |
0,28 |
12,5 |
0,445 |
6,741573034 |
4 |
4 |
0,7 |
0,44 |
17,5 |
0,569 |
7,029876977 |
5 |
5 |
0,9 |
0,59 |
23 |
0,674 |
7,418397626 |
6 |
6 |
1,2 |
0,87 |
30 |
0,789 |
7,604562738 |
7 |
7 |
1,5 |
1,06 |
37,5 |
0,869 |
8,055235903 |
8 |
8 |
1,8 |
1,26 |
45 |
0,931 |
8,592910849 |
9 |
9 |
2,1 |
1,58 |
52,5 |
0,994 |
9,054325956 |
10 |
10 |
2,4 |
1,74 |
60 |
1,053 |
9,496676163 |
11 |
11 |
2,7 |
1,94 |
67,5 |
1,094 |
10,05484461 |
Jeśli ogrzewamy jakiekolwiek ciało w pewnym punkcie, to zawsze stwierdzimy po pewnym czasie ogrzanie sąsiednich punktów tego ciała lub też innych ciał znajdujących się w pobliżu. Dowodzi to, że energia cieplna przenosi się z jednych punktów do drugich. Przenoszenie to odbywać się może trzema różnymi sposobami:
Każde ciało znajdujące się w temperaturze O K promieniuje do otoczenia energię, którą można określić w następujący sposób:
![]()
Stosunek zdolności emisyjnej ciała E(lambda,T) do jego zdolności absorpcyjnej a(lambda,T) jest dla wszystkich ciał taką samą funkcją zależną od długości emitowanego promieniowania i temperatury ciała.
Prawo Kirchoffa.
I równanie przewodnictwa (równanie Fouriera):
![]()
![]()
K - współczynnik przewodnictwa cieplnego
II równanie przewodnictwa (szybkość przewodnictwa ciepła):
![]()
Hc - przewodnictwo termometryczne.
![]()
Rozszerzalność liniowa w zależności od temperatury przedstawia się następująco:
Jest to zależność liniowa. Współczynnik alfa nosi nazwę współczynnika temperaturowego rozszerzalności liniowej.
Przyrost długości pręta jest wprost proporcjonalna do przyrostu temperatury. Całkowita długość pręta podczas jego ogrzania o delta T wzrośnie o :
![]()
a wartość każdej jednostki długości pręta ogrzanego o 1 K wzrośnie o :
![]()
Wielkość a nazywamy współczynnikiem termicznym rozszerzalności liniowej . Jak widać z równania powyżej, współczynnik rozszerzalności liniowej jest równy stosunkowi długości do iloczynu pierwotnej długości i przyrostu temperatury.
Uwzględniając, że:
![]()
otrzymamy z powyższych wzorów wzór na długość pręta w temperaturze T:
![]()
Powyższa zależność stosuje się dokładnie tylko w niewielkim zakresie temperatur, stanowi bowiem pierwsze przybliżenie.
Dokładne pomiary wykazują, że należałoby stosować wyrażenia zawierające zależność długości również o kwadratu, a nawet i od sześcianu przyrostu temperatury, a więc typu :
![]()
przy czym współczynnik beta jest na ogół znikomo mały i wywiera wpływ tylko przy stosunkowo dużych zmianach temperatury.
W miarę wzrostu temperatury wszystkie wymiary ciała rosną w tym samym stosunku, wobec tego rośnie też jego powierzchnia i objętość. W związku z tym można wprowadzić pojęcie współczynnika rozszerzalności powierzchniowej i objętościowej.
W ćwiczeniu wykorzystywane jest zjawisko termoelektryczne Seebecka, które polega na wystąpieniu siły elektromotorycznej w obwodzie złożonym z dwóch kawałków różnych metali, których połączone końce znajdują się w różnych temperaturach. Sam taki obwód złożony z połączonych ze sobą na końcach kawałków dwóch różnych metali nazywamy termoparą. Wielkość siły termoelektryczną występują w termoparze opisuje prawo Avenariusa:
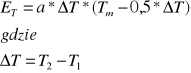
Oznacza różnicę temperatur pomiędzy końcami termopary, a jest stałą charakterystyczną dla danej pary metali, zaś Tm jest temperaturą punktu neutralnego - jest to temperatura gorętszego spojenia termopary, przy której występuje największa siła termoelektryczna dla zadanej temperatury chłodniejszego spojenia.
Siłę termoelektryczną występującą w termoparze można mierzyć włączając w obwód woltomierz. Ma w tym przypadku zastosowanie prawo trzeciego metalu tzn. wprowadzenie do obwodu metali A i B trzeciego metalu C nie wpływa na wartość wypadkowej siły termoelektrycznej, pod warunkiem, że oba końce przewodu z metalu C znajdują się w takiej samej temperaturze.
Jeżeli do końców przewodnika doprowadzimy napięcie U, to wytworzone w ten sposób pole elektryczne spowoduje przepływ prądu a natężeniu I. Prawo Ohma mówi, że stosunek napięcia między dwoma punktami przewodnika do natężenia przepływającego przezeń prądu jest wielkością stałą i nie zależy ani od napięcia ani od natężenia prądu. Stosunek ten nazywamy oporem:
![]()
Opór elektryczny przewodnika zmienia się wraz z temperaturą; w przypadku przewodników metalicznych opór ten w miarę wzrostu temperatury wzrasta, w przypadku półprzewodników (węgiel i inne) i elektrolitów - maleje. Niektóre stopy mogą wykazywać stałość oporu przy zmianach temperatury. Wielkością charakteryzującą zmiany temperaturowe oporu danego przewodnika jest współczynnik temperaturowy a (alfa). Wyraża on ze względny przyrost oporu:
![]()
Przy ogrzaniu przewodnika o 1stopień C. Jeśli przyrost oporu spowodowany ogrzaniem od 0 do t stopni, to współczynnik a (alfa) możemy określić zależnością:
![]()
Współczynnik a możemy zatem wyznaczyć na podstawie tego wzoru, jeśli zmierzony zostanie opór R0 w temperaturze 0 stopni C i opór Rt w temperaturze t.
Niejednokrotnie zdarza się tak, że możemy natomiast zmierzyć opór R0, bo nie dysponujemy lodem; możemy natomiast zmierzyć opór w dwu różnych od zera temperaturach t1 i t2. Posługujemy się wówczas wzorem na współczynnik a, wyprowadzonym w sposób następujący:
Z równania wynika, że zależność oporu od temperatury jest następująca:
![]()
Mając opory R1 i R2 tego samego przewodnika w temperaturach t1 i t2 możemy napisać dwa równania:
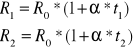
Dzieląc te równania stronami otrzymujemy wzór na współczynnik alfa:
![]()
![]()
I Prawo Ohma :
II Prawo Ohma :
![]()
gdzie:
l - długość przewodnika
s - powierzchnia przekroju
Lokalne Prawo Ohma :
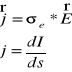
gdzie: j - gęstość prądu
Schemat obwodu pomiarowego:
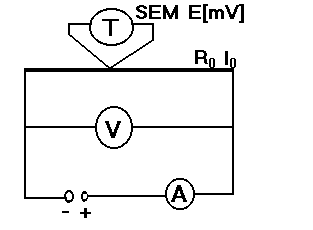
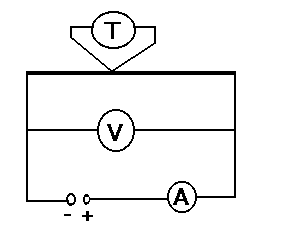
Ćwiczenie rozpoczynamy od sprawdzenia połączeń układu. Następnie wyznaczamy długość początkową drutu i zerujemy czujnik zegarowy. Włączamy zasilanie. Następnie zmieniamy napięcie co 1 V (do 10 V) i notujemy po ustaleniu się temperatury drutu SEM termopary E, przyrost długości, napięcie U oraz natężenie prądu I.
Wyniki:
Wykonując pomiary dwu wielkości x i y uzyskujemy pary liczb (xi, yi) i naszym zadaniem jest znaleźć równanie prostej najlepiej „pasującej” do nich. Niech równanie to będzie miało postać:
y = a * x + b
a „dopasowanie” zgodnie z metodą najmniejszych kwadratów oznacza, że:
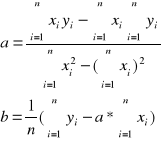
![]()
gdzie a i b są empirycznymi współczynnikami regresji liniowej, Poszukując ekstremum związanego powyższego równania udowadnia się, że:
gdzie i = 1,2,3,4,...,n czyli n jest ilością par punktów (xi, yi).

Na odchylenie standardowe S(a) i S(b) będące miarą niepewności pomiarowych współczynników regresji a i b otrzymuje się następujące równania:
Kryterium tego jak punkty pomiarowe (xi, yi) potwierdzają liniową zależność pomiędzy wielkościami x i y, stanowi wartość tzw. współczynnika korelacji liniowej p. Jego wartość zmienia się w granicach od 1 do 0. Gdy p=1, to dopasowanie jest idealne. Gdy p=0, to zależność liniowa pomiędzy xi i yi nie istnieje.
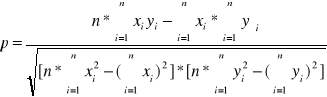
Dla pierwszego wykresu ![]()
:
T [K] - x |
l [mm] y |
|
|
x * y |
2,5 |
0,03 |
6,25 |
0,0009 |
0,075 |
7,5 |
0,13 |
56,25 |
0,0169 |
0,975 |
12,5 |
0,28 |
156,25 |
0,0784 |
3,5 |
17,5 |
0,44 |
306,25 |
0,1936 |
7,7 |
23 |
0,59 |
529 |
0,3481 |
13,57 |
30 |
0,87 |
900 |
0,7569 |
26,1 |
37,5 |
1,06 |
1406,25 |
1,1236 |
39,75 |
45 |
1,26 |
2025 |
1,5876 |
56,7 |
52,5 |
1,58 |
2756,25 |
2,4964 |
82,95 |
60 |
1,74 |
3600 |
3,0276 |
104,4 |
Suma |
||||
|
7,98 |
11741,5 |
9,63 |
335,72 |
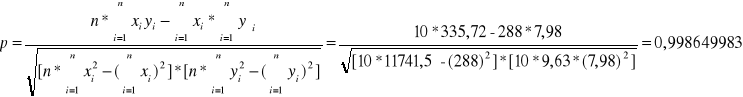
Równanie prostej : y = 0,027562515 * x + 0,004199558
Współczynnik korelacji liniowej : p = 0,998649983
Dla drugiego wykresu![]()
:
T [K] - x |
R - y |
|
|
x * y |
2,5 |
6,609385327 |
6,25 |
43,6839744 |
16,52346332 |
7,5 |
6,153846154 |
56,25 |
37,86982249 |
46,15384615 |
12,5 |
6,741573034 |
156,25 |
45,44880697 |
84,26966292 |
17,5 |
7,029876977 |
306,25 |
49,41917031 |
123,0228471 |
23 |
7,418397626 |
529 |
55,03262334 |
170,6231454 |
30 |
7,604562738 |
900 |
57,82937443 |
228,1368821 |
37,5 |
8,055235903 |
1406,25 |
64,88682546 |
302,0713464 |
45 |
8,592910849 |
2025 |
73,83811685 |
386,6809882 |
52,5 |
9,054325956 |
2756,25 |
81,98081851 |
475,3521127 |
60 |
9,496676163 |
3600 |
90,18685815 |
569,8005698 |
Suma |
||||
288 |
76,75679073 |
11741,5 |
600,1763909 |
2402,634864 |
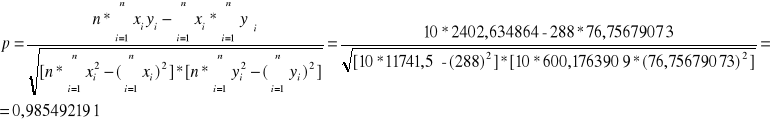

Równanie prostej : y = 0,27672231 * x - 0,293923693
Współczynnik korelacji liniowej : p = 0,985492191
Wyniki:
Odczytując z wykresów odpowiednie wartości otrzymujemy:
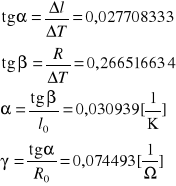
![]()
![]()
![]()
![]()
![]()
![]()
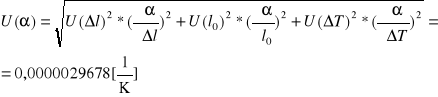
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
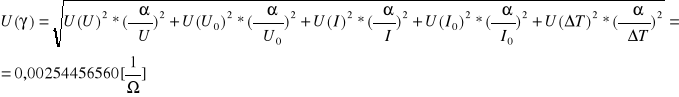
![]()
![]()
1
8
![]()
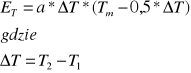
![]()
![]()
![]()
![]()
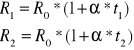
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
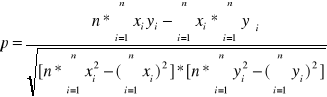

![]()
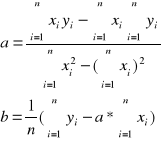
![]()
![]()
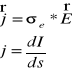
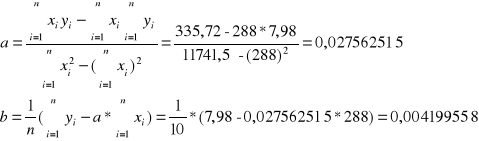
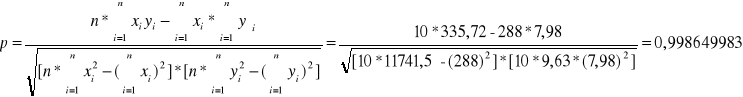

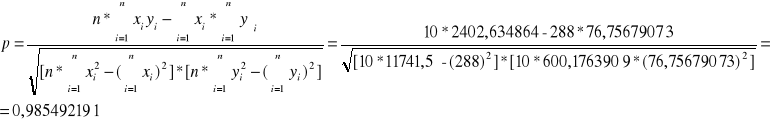
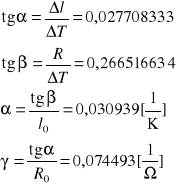
Wyszukiwarka
Podobne podstrony:
modu- younga - opracowanie, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - labo
lab 361i 29 listopada 2002, studia,
laborka44, studia, fizyka, laborka z fizy, Laborki
laborka35, studia, fizyka, laborka z fizy, Laborki
modu- younga - teoria, Studia PWr W-10 MBM, Semestr II, Fizyka, Fizyka - laborki, Fizyka - laborki,
33, Studia, Fizyka, LABORKI, fizyka spr
24[2]. moje OBLICZENIA, Studia, Fizyka, LABORKI
Ćwiczenie nr 17, Studia, Fizyka, LABORKI
Ćwiczenie1 42, Studia, Fizyka, LABORKI
czasy gramatyczne, Studia, Fizyka, LABORKI
więcej podobnych podstron