Wyprowadzenie wzoru :

Załóżmy, że lewy koniec belki jest zamocowany poziomo, a do jej prawego

końca przykładamy siłę (obciążenie). Pod wpływem działania tej siły belka ugnie się w sposób pokazany na rysunku. Górne warstwy belki wydłużają się, a warstwy dolne ulegają skróceniu. W środku wysokości belki istnieje tzw. warstwa obojętna W, której długość nie ulegnie zmianie. Zarówno do wydłużenia, któremu ulega górna część belki, jak i skróceniu (część dolna) stosuje się prawo Hooke'a. Oznaczmy przez s strzałkę ugięcia, czyli odchylenie prawego końca belki od położenia belki nieobciążonej. Będę obserwować, jakim zmianom na skutek ugięcia ulegają przekroje p i q, odległe od punktu zamocowania belki o x oraz (x +
x). Przed odkształceniem belki przekroje te były równoległe do siebie, a po ugięciu tworzą kąt
. Przez punkt, w którym płaszczyzna q przecina warstwę W przeprowadzimy płaszczyznę q' równoległą do płaszczyzny p. Na skutek ugięcia warstwa V, znajdująca się w odległości y od warstwy W, wydłuża się o
. Przekrój powierzchni prostopadłej do długości belki wynosi b
. Siła powodująca odkształcenie tego elementu wyraża się wzorem:

(
)

(
)

(
)

Moment siły względem warstwy W wynosi:

Sumując powyższe wyrażenie na wszystkie wartości y otrzymamy:

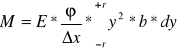
Jeżeli ponadto wprowadzimy oznaczenie:

(****)

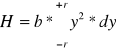
to ostatnie równanie przyjmie postać:

(*)

Belkę odkształca moment pochodzący od zewnętrznej siły F

gdzie l oznacza długość belki, a wyrażenie w nawiasie kwadratowym jest ramieniem przekroju q. Po zaniedbaniu małej wielkości
ostatnie równanie przyjmie postać:

(**)

Kąt
zawarty jest również między stycznymi do belki w punktach, w których przekroje p i q przecinają górną powierzchnię belki; zatem możemy napisać:

(***)

Porównując równania (*) i (**) oraz uwzględniając związek (***), otrzymamy:

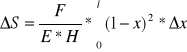
a po scałkowaniu:

Wartość współczynnika H zależy od kształtu i wymiarów geometrycznych belki.

W przypadku, gdy przekrój belki posiada kształt prostokąta o wysokości h i szerokości b to równanie (****) przyjmie postać:

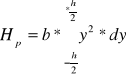
po scałkowaniu:

Całkowanie podobnego wyrażenia dla kołowego przekroju belki daje:

Podstawiając wzory na H_P i H_K do wzoru na strzałkę ugięcia, otrzymamy wzory dla belki jednostronnie zamocowanej o przekroju prostokątnym i wysokości h oraz dla belki okrągłej o promieniu r:

Wzór na strzałką można również stosować w przypadku, gdy belka jest podparta na dwóch końcach i obciążona w środku siłą F. Belka zachowuje się wtedy w taki sposób, jak gdyby była zamocowana w środku, a na każdy z jej końców działa siła F/2 skierowana ku górze. Siła F/2 działa wtedy na połowę belki - l/2.

Podstawiając do wzoru na strzałkę ugięcia zamiast długości l wartość l/2 oraz zamiast siły F wartość F/2, otrzymamy nowy wzór na strzałkę ugięcia:

Gdy podstawimy do powyższego wzoru wyrażenia na H odpowiednio dla belki o przekroju prostokątnym i okrągłej otrzymamy:

- 1 -

1

---