Tatiana Zaszkowska 15 XI 2001

Ćwiczenie nr 24

Temat: Badanie obwodu RLC.

Teoria

Obwodem RLC nazywamy obwód zawierający kondensator o pojemności C, cewkę o indukcyjności L i oporze R. Obecność tego oporu powoduje, że w każdym cyklu w obwodzie wydziela się ciepło Joule'a, energia obwodu maleje i drgania zanikają. Otrzymujemy w ten sposób drgania swobodne tłumione. Współczynnik tłumienia wyraża się wzorem:

. W obwodzie zawierającym opór można uzyskać drgania niezanikające, nazywane drganiami wymuszonymi. Należy wówczas podłączyć zmienną SEM zwaną siłą wymuszającą:

. Drgania w obwodzie mają maksymalną amplitudę, gdy pulsacja
ma wartość:
. Równanie drgań w obwodzie RLC ma postać:

Ćwiczenie polega na pomiarze natężeń prądu przy odpowiednich częstotliwościach generowanych przez generator. Układ łączymy według schematu.

Wyprowadzenie wzorów roboczych.

Wiadomo, że:

(*)

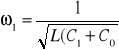
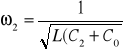
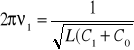
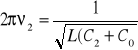
Podnosząc do kwadratu i obliczając L z obydwu równań otrzymujemy:

Ostatecznie:

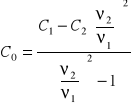
Drugi wzór otrzymujemy z relacji (*):

Obliczenia:

Częstość rezonansowa wynosi:

Dla C₁=510pF
₁=760kHz

Dla C₂=200pF
₂=1160kHz

Pojemność własna obwodu wynosi:

C₀=33,14583334pF

Indukcyjność zwojnicy wynosi:

L=0,080741465mH

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla C₁ i C₂:

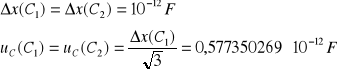
Niepewność całkowita dla
i
:

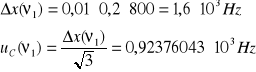
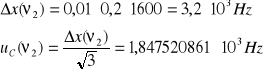
Aby obliczyć pochodne cząstkowe przekształcę wzór roboczy następująco:

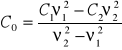
Wartości pochodnych cząstkowych C₀ względem poszczególnych zmiennych:

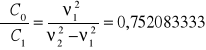
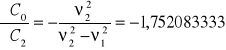
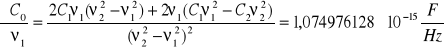
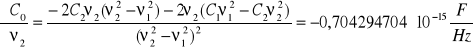
Niepewność całkowita dla C₀:

Niepewność rozszerzona ( dla
=0,95 k=2 ) wynosi:

Wartości pochodnych cząstkowych L względem poszczególnych zmiennych:

Niepewność całkowita dla L:

Niepewność rozszerzona ( dla
=0,95 k=2 ) wynosi:

Ostateczne wyniki po zaokrągleniu do dwu miejsc znaczących:

Pojemność własna obwodu

Indukcyjność zwojnicy

---