Tomasz Pajączkowski

11.04.2001

Ćwiczenie nr 13.

Temat: Wyznaczanie napięcia powierzchniowego cieczy metodą naczyń włosowatych.

Celem ćwiczenia jest wyznaczenie współczynnika napięcia powierzchniowego wody metodą naczyń włosowatych, a następnie wyznaczenie promieni naczyń połączonych użytych przy wykonaniu ćwiczenia

Tabela:

	seria pomiarowa
[ cm ]	1)	2)	3)	4)	5)	6)			7)					8)	Σ	wartość średnia
h-00	39,16	39,09	39,16	39,09	39,15	39,08			39,17					39,05	312,95	39,12
h0	36,18	35,95	36,11	36,16	35,99	35,16			35,99					36,11	287,65	35,96
h1	36,88	36,84	36,82	36,85	36,7	36,83			36,89					36,78	294,59	36,82
h2	37,42	37,62	37,64	37,63	37,93	37,6			37,86					37,56	301,26	37,66
h3	38,5	38,38	38,4	38,36	38,39	38,42			38,4					38,4	307,25	38,41
h4	39,12	39,02	39,12	39,04	39,26	39,12			39,3					39,16	313,14	39,14
h5	39,95	39,83	39,75	39,84	39,93	39,86			39,86					39,85	318,87	39,86

Teoria zjawiska:

Pomiędzy drobinami cieczy działają siły van der Waalsa zwane również siłami spójności, a ich wielkość zależy od odległości pomiędzy drobinami. Cząsteczki znajdujące się w warstwie powierzchniowej równej promieniowi sfery działania sił międzycząsteczkowych znajdują się pod działaniem sił wciągających je do wnętrza cieczy. Warstwa powierzchniowa przybiera możliwie najmniejszą powierzchnię.

Aby określić wartość napięcia powierzchniowego, skupić się należy na wycinku powierzchni cieczy ΔS. Wycinek ten ma skłonność do zmiany swojej powierzchni, działając pewną siłą na sąsiednie odcinki powierzchni cieczy. Siła ta nosi nazwę siły napięcia powierzchniowego i jest skierowana prostopadle do ograniczenia cieczy, a stycznie do jej powierzchni.

Stosunek siły napięcia powierzchniowego do długości ograniczenia powierzchni nazywamy napięciem powierzchniowym i oznaczamy σ.

Napięcie powierzchniowe maleje ze wzrostem temperatury i dla temperatury krytycznej jest równe zero.

Napięcie powierzchniowe wiąże się z pracą wykonaną wbrew siłą spójności, potrzebną do zwiększenia swobodnej powierzchni cieczy. W związku z powyższym można zapisać następującą zależność: σ = W/ΔS.

W powyższym przedstawiłem zjawiska zachodzące na granicy ciecz i gaz, związane z cząsteczkową budową cieczy. Siły spójności działające między cząsteczkami ciecz, gazu lub ciała stałego a cząsteczkami jakiegoś ciała stałego prowadzą do zjawiska przylegania.

Za miarę przylegania cieczy do ciała stałego należy przyjąć pracę W potrzebną do oderwania cieczy od ciała stałego o powierzchni 1 m². Należy przy tym uwzględnić zarówno siły, które wywierają na siebie cząsteczki cieczy, jak i siły oddziaływania cząsteczek cieczy i ciała stałego.

Odróżniamy tu dwa skrajne przypadki: a) przyleganie cieczy niezwilżającej, b) przyleganie cieczy zwilżającej ( na rysunkach poniżej przedstawiono przypadki kształtu cieczy ).

W przypadku cieczy zwilżającej siły oddziaływania cząsteczek są mniejsze niż siły spójności między cząsteczkami cieczy i ciała stałego.

Dla cieczy niezwilżającej siły spójności cząsteczek cieczy są mniejsze niż siły spójności między cząsteczkami cieczy i ciała stałego.

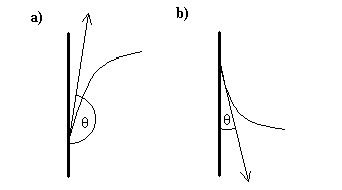
Kształt powierzchni cieczy przy ściankach naczynia: a) ciecz niezwilżająca, b) ciecz zwilżająca

Napięcie powierzchniowe cieczy i przyleganie cieczy do ścianek powoduje wystąpienie zjawiska włosowatości, wznoszenia lub opadania cieczy, które występuje najwyraźniej w cienkich rurkach ( włoskowatych ). Zjawisko to wygląda inaczej, gdy ciecz ich ścianek nie zwilża, a inaczej gdy je zwilża. Gdy ciecz znajduje się w wąskiej rurce, kształt powierzchni granicznej między cieczą i gazem jest wklęsły dla cieczy zwilżającej, a wypukły dla cieczy niezwilżającej ( co pokazano na rysunkach poniżej ).

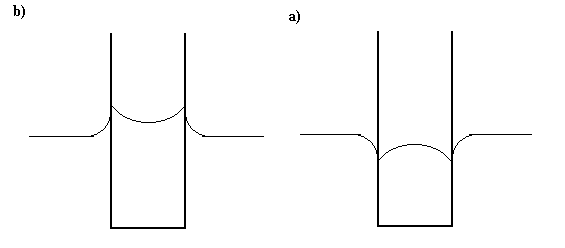
Meniskiem nazywamy ową wygiętą powierzchnię cieczy. Menisk bywa wypukły lub wklęsły.

Siły powierzchniowe powodujące wzniesienie słupka działają na obwodzie kapilary ( 2πr ) i wynoszą: F = 2πrσ.

Opis metody z opisem przeprowadzonego eksperymentu:

Celem powyższego ćwiczenia było wyznaczenie napięcia powierzchniowego wody przy panujących warunkach atmosferycznych. Dokonałem tego przy użyciu naczyń połączonych wykorzystujących zjawiska kapilarne. Przy wykorzystaniu tej metody pomiar sprowadza się do wyznaczenia różnicy wysokości słupa cieczy kapilary ( h-00 ) zanurzonej w cylindrze wzorcowym w stosunku do poziomu cieczy w tym cylindrze ( h0 ). Pomiaru tego dokonać można na różne sposoby. W powyższym ćwiczeniu dokonałem tego przy pomocy lunety umieszczonej na wyskalowanym statywie. Pozwalało to, na odczytanie wysokości po przednim ustawieniu celownika lunety na menisk dolny cieczy kapilary.

Uzyskane wartości zebrałem w tabeli, a następnie na ich podstawie obliczyłem napięcie powierzchniowe wody w panujących warunkach atmosferycznych.

Druga część ćwiczenia polegała na wyznaczeniu promieni pozostałych naczyń w oparciu o wyznaczoną wartość napięcia powierzchniowego. W tym celu konieczne było wyznaczenie wysokości słupa cieczy w tych naczyniach, co też uczyniłem. Pomiary wysokości słupków cieczy naczyń połączonych wykonałem w sposób analogiczny jak powyżej.

Otrzymane wartości zebrałem w powyższej tabeli, a następnie na ich podstawie dokonałem obliczeń i wyciągnąłem końcowe wnioski.

Wyprowadzenie wzoru roboczego:

Siły powierzchniowe powodujące wzniesienie słupka działają na obwodzie kapilary ( 2πr ) i wynoszą: F = 2πrσ. Są one równoważone ciężarem słupa wody o wysokości h ( F= πr²hρg).

Przyrównując powyższe wartości otrzymujemy:

πr²hρg = 2πrσ

σ = 1/2·rhgρ gdzie: h = h-00 - h0 = Δh

Obliczenia do wykonanego ćwiczenia:

σ = 0,5·( 39,12 -35,96 )·0,5·10^-3·9,81·1000 = 77,50·10^-3 N/m

{ działanie na jednostkach: m·m·m/s²·kg/m³ = mkg/s²m = N/m

σ = Δhrgρ/2

r = 2σ/Δhgρ

Po podstawieniu do powyższego wzoru wartości otrzymałem:

r1 = 0,0018 m = 2 mm

r2 = 0,00093 m = 1 mm

r3 = 0,000645 m = 0,65 mm

r4 = 0,000497 m = 0,5 mm

r5 = 0,000405 m = 0,4mm

Szacowanie niepewności pomiaru:

U_C(g) = 0,0058 m/s²

U_C(r) = 0,1·10^-3/3^1/2 = 5,8·10^-5 m

U_C(ρ) = 1·10^-3/3^1/2 = 0,58 kg/m³

U_C(Δh) = 0,01·10^-3/3^1/2 = 5,8·10^-5

[ ðσ/ðΔh = rgρ/2 = 2,45 kg/s²m]² = 6,01 kg²/s⁴m²

[ ðσ/ðr = Δhgρ/2 = 155 kg/s²m]² = 2402 kg²/s⁴m²

[ ðσ/ðg = rΔhρ/2 = 0,0079 kg/m]² = 6,24·10^-5 kg²/m²

[ ðσ/ðρ = rΔhg/2 = 7,75·10^-5 m³/s²]² = 6,01·10^-9 m⁶/s⁴

U_C(σ) = [ ( ðσ/ðh )²·U²_C(h) + ( ðσ/ðr )²·U²_C(r) + ( ðσ/ðg )²·U²_C(g) + ( ðσ/ðρ )²·U²_C(ρ) ]^1/2 =

= 2,85·10^-3 N/m

dla α = 0,95

U_C = 5,7·10^-3 N/m

σ = ( 77,50 ± 5,70 )·10^-3 N/m

Szacowanie niepewności pomiaru przy wyznaczaniu promieni naczyń połączonych:

1. ðr/ðσ = 2/Δhgρ = ... m²/kg·s²

2. ðr/ðΔh = 2σ/ρgΔh² = ... 1

3. ðr/ðg = 2σ/ρg²Δh = ... s²

4. ðr/ðρ = 2σ/ρ²gΔh = ... m⁴/kg

Wartości wyliczone zgodnie z powyższymi wzorami ze względów estetycznych umieściłem w poniższej tabeli a następnie na ich podstawie wyznaczyłem błąd pomiaru dla każdej wartości r.

1)	0,0002375	0,0001202	0,0000834	0,0000642	0,0000524
2)	-0,0000214	-0,0000055	-0,0000026	-0,0000016	-0,0000010
3)	-0,0000019	-0,00000095	-0,00000066	-0,00000051	-0,00000041
4)	-0,000000018	-0,0000000093	-0,0000000065	-0,000000005	-0,0000000041

{ jednostki jw.

U(g)={(ðr/ðσ)²·U_C²(σ)+(ðr/ðΔh)²·U_C²(Δh)+(ðr/ðg)²·U_C²(g)+(ðr/ðρ)²·U_C²(ρ)}^1/2= ... m

0,000058

0,000058

0,000058

0,000058

0,000058

{ jednostki jw.

dla α = 0,95 U_C(g) = 2·U(g) = 0,00012 m = 1,2·10^-4 m

r1 = 0,0018 ± 0,00012m = 2,00 ± 0,12 mm

r2 = 0,00093 ± 0,00012m = 1,00 ± 0,12 mm

r3 = 0,000645 ± 0,00012 m = 0,65 ± 0,12 mm

r4 = 0,000497 ± 0,00012 m = 0,50 ± 0,12 mm

r5 = 0,000405 ± 0,00012 m = 0,40 ± 0,12 mm

Wnioski:

Wyznaczony współczynnik napięcia powierzchniowego wynosi: σ = ( 77,50 ± 5,70 )·10^-3 N/m. Wartość ta nieznacznie różni się od wartości odczytanej z tablic dla temperatury 20°C, która to wynosi σ = 72,75·10^-3 N/m, co dowodzi poprawności wykonanego ćwiczenia.

Na końcowy wynik wpływ miał niewątpliwie fakt, że powyższe ćwiczenie wykonywane było w zespole dwuosobowym ( każda z osób wykonała cztery serie pomiarów ), co skutkuje różną dokładnością wyznaczonych wartości.

Wyznaczone promienie naczyń połączonych wynoszą odpowiednio:

r1 = 2,00 ± 0,12 mm

r2 = 1,00 ± 0,12 mm

r3 = 0,65 ± 0,12 mm

r4 = 0,50 ± 0,12 mm

r5 = 0,40 ± 0,12 mm

Wartości te są przybliżone do wartości najbardziej prawdopodobnych.

Stałe:

T = 21,5°C

P = 754 mmHg

r = 05 mm

ρ = 0,998 g/cm³

---