Schemat stanowiska
Wzory wyjściowe i wynikowe
Strumień objętości obliczam z zależności:
![]()
Aby obliczyć prędkość cieczy korzystam z zależności:
![]()
Podstawowym wzorem, z którego wyznaczamy liczbę Reynoldsa Re jest:
![]()
gdzie:
![]()
Sumę strat miejscowych w punktach 1, 3 i 4 obliczam z zależności:
![]()
Straty liniowe na kapilarach ![]()
i ![]()
wynoszą (na podstawie wzoru Darcy'ego - Weisbacha):
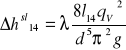
Doświadczalnie współczynnik oporu liniowego ![]()
wyznaczam na z zależności:
![]()
![]()
![]()
Otrzymuję następujący wzór:
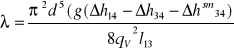
Teoretyczny współczynnik oporu liniowego ![]()
obliczam z zależności:
![]()
Tabela pomiarowa
|
|
|
|
|
|
|
|
|
|
|
|
mm |
mm |
cm3 |
s |
cm3/s |
m/s |
- |
- |
mm |
mm |
mm |
- |
1204 |
709 |
50 |
40,87 |
1,22 |
0,97 |
1275 |
0,0502 |
143 |
854 |
72 |
0,0640 |
1099 |
648 |
50 |
44,87 |
1,11 |
0,88 |
1161 |
0,0551 |
119 |
778 |
59 |
0,0713 |
794 |
471 |
50 |
59,31 |
0,84 |
0,67 |
878 |
0,0729 |
68 |
589 |
34 |
0,0920 |
629 |
375 |
50 |
72,66 |
0,69 |
0,54 |
717 |
0,0893 |
45 |
480 |
23 |
0,1105 |
498 |
297 |
25 |
44,16 |
0,57 |
0,45 |
590 |
0,1085 |
31 |
395 |
15 |
0,1310 |
490 |
294 |
25 |
44,31 |
0,56 |
0,45 |
588 |
0,1089 |
30 |
394 |
15 |
0,1285 |
406 |
243 |
25 |
53,57 |
0,47 |
0,37 |
486 |
0,1316 |
21 |
326 |
10 |
0,1585 |
327 |
196 |
25 |
66,1 |
0,38 |
0,30 |
394 |
0,1624 |
14 |
264 |
7 |
0,1963 |
265 |
159 |
25 |
80,37 |
0,31 |
0,25 |
324 |
0,1975 |
9 |
217 |
5 |
0,2370 |
200 |
118 |
25 |
98,75 |
0,25 |
0,20 |
264 |
0,2426 |
6 |
177 |
3 |
0,2786 |
142 |
86 |
25 |
144,59 |
0,17 |
0,14 |
180 |
0,3552 |
3 |
121 |
1 |
0,4129 |
![]()
Oznaczenia symboli:
![]()
- wysokość strat ciśnienia na odcinku 14
![]()
- wysokość strat ciśnienia na odcinku 34
![]()
- wysokość strat miejscowych na odcinku 14
![]()
- wysokość strat liniowych na odcinku 14
![]()
- liczba Reynoldsa
![]()
- objętość cieczy
![]()
- czas przepływu cieczy
![]()
- kinematyczny współczynnik lepkości
![]()
- strumień objętości
![]()
- szybkość przepływu cieczy
![]()
- wartość średnia strumienia objętości
![]()
- średnica rury
![]()
- temperatura wody
![]()
- współczynnik strat miejscowych w przepływie ze zbiornika do rury
![]()
- współczynnik strat miejscowych w przepływie z rury do zbiornika
![]()
- współczynnik oporu liniowego
Dane, przydatne do obliczeń:
![]()
![]()
![]()
![]()
![]()
![]()
Przykładowe obliczenia
Dla pierwszego pomiaru obliczenia wyglądają następująco:
Strumień objętości:
![]()
Prędkość cieczy:
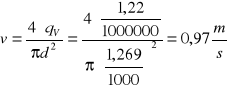
Liczba Reynoldsa Re wynosi:
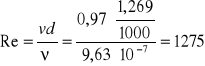
Kinematyczny współczynnik lepkości obliczam na podstawie wzoru:
![]()
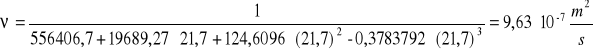
Teoretyczny współczynnik oporu liniowego ![]()
:
![]()
Sumę strat miejscowych w punktach 1, 3 i 4 obliczam z zależności:
![]()
Straty liniowe na kapilarach ![]()
i ![]()
wynoszą (na podstawie wzoru Darcy'ego - Weisbacha):
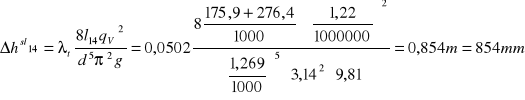
Doświadczalnie współczynnik oporu liniowego ![]()
:
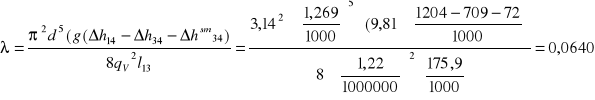
Wykresy
Wnioski
Wraz ze wzrostem liczby Reynoldsa wartość współczynnika oporu liniowego
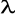
maleje.
Niewielkie przesunięcie wykresu doświadczalnego w stosunku do teoretycznego wynika z niedokładności pomiarów oraz przybliżeń przyjętych w obliczeniach.
Zależności wysokości strat miejscowych i liniowych (zobrazowane na drugim wykresie) są zależnościami wielomianowymi drugiego stopnia, co wynika z użytych wzorów.
Linie trendu wyznaczają dalszą część wykresu, których początek przecina się w początku układu współrzędnych. Jest to efektem tego, że gdy strumień objętości wynosi zero (ciecz nie płynie) nie może być żadnych strat wysokości ciśnienia.
Naczynie Marinota ułatwiło utrzymanie stałego strumienia objętości powietrza, dzięki czemu pomiary stały się dokładniejsze.
Niedokładności pomiarów mogą wynikać z opóźnionego czasu reakcji podczas pomiaru czasu przepływu danej objętości cieczy oraz nieidealnego oka ludzkiego. Mogą one też być wynikiem długiego czasu stabilizowania się ciśnień w manometrach (odczyt
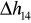
i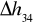
).
Wyszukiwarka
Podobne podstrony:
N12, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
n9-Aga, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N10, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N17, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N2, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N14, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N4, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N7, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
plyny4, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N19, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N13, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
N21, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny, laborki
WAZne PLYNY N10, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, płyny
MIUE koło 0 gr2, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, maszyny i urz elektr, maszyny,
ćw 20-21, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, terma
ćw 24, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, terma
POLITECHNIKA WROCLAWSK1, PWr W9 Energetyka stopień inż, IV Semestr, sprawka, maszyny i urz elektr, m
więcej podobnych podstron