Imię i nazwisko	Katarzyna Ciereszko
Grupa	I8E1S1

Uwaga:

• integralną część sprawozdania stanowią wybrane pliki pakietów GRETL i EXCEL (jeżeli takie będą), zawierające szczegółowe obliczenia związane z rozwiązywanym zadaniem,

• wszystkie formalne zależności (wzory) wpisywać za pomocą edytora równań,

• wszystkie pola tabel oraz wyróżnione miejsca w tekście muszą być wypełnione.

1. Identyfikacja szeregu czasowego

1. Testy istnienia trendu

Nazwa testu	Wartość sprawdzianu	Wartość krytyczna testu	Występowanie trendu (TAK/NIE)
Analiza wzrokowa wykresu szeregu czasowego			Tak
Test współczynnika korelacji Pearsona	-6,38226	1,9826	Nie
Testu Danielsa dla dużych liczebności szeregu czasowego n	-6,05197	1,9826	Nie
Ostateczna decyzja			Nie

2. Test Fiszera stopnia wielomianu modelującego trend

Stopień wielomianu k	Wariancja resztowa wielomianu rzędu k	Wartość sprawdzianu dla wielomianu rzędu k i k+1	Wartość krytyczna testu	Modelem trendu jest wielomian rzędu n (TAK/NIE)
0
1
2
3
4
Ostateczna decyzja

2. Analiza wahań sezonowych

W tym miejscu umieścić korelogram

Zidentyfikowana liczba faz w cyklu wahań sezonowych (okresowość wahań sezonowych)

4

3. Model Kleina

1. Model pierwotny

• Postać modelu

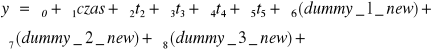
• Istotność parametrów strukturalnych

Parametr	Wartość parametru	Wartość testu	Wartość krytyczna testu	Ocena istotności (Tak/Nie)
	113,974	8,567	1,984	Tak
	-4,43023	-1,826			Tak
	0,113677	0,8338			Tak
	-0,00229302	-0,7269			Nie
	2,34541e-05	0,7365			Nie
	-8,62529e-08	-0,7417			Nie
	47,8219	13,53			Tak
	31,5223	8,941			Tak
	-15,5127	-4,400			Tak

1. Model końcowy

• Postać modelu




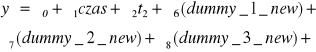
Parametr	Wartość parametru	Wartość testu	Wartość krytyczna testu
	106,893	17,39	1,983
	-2,80612	-10,78
	0,0170053	7,350
	47,9977	13,78
	31,5805	9,067
	-15,5706	-4,470

4. Prognoza szeregu czasowego

1. Prognoza

• Wartości zmiennych objaśniających:

Nazwy zmiennych objaśniających	czas	T2	Dummy_1_new	Dummy_2_new	Dummy_3_new
Wartości w okresie prognozy T = n+1	109	11881	1	0	0
Wartości w okresie prognozy T = n+2	110	12100	0	1	0

• Wartość szeregu czasowego w okresie T = n+2:-19,4

1. Błędy prognozy ex post:

• Tabela pomocnicza:

t	Wartości szeregu czasowego	prognoza wygasła	Błąd prognozy wygasłej
n-9	-35,5	-19,8	-15,7
n-8	-51,6	-67,7	16,1
n-7	82,4	44,9	37,5
n-6	48,0	29,2	18,8
n-5	-28,5	-17,3	-11,2
n-4	-65,5	-65,0	-0,5
n-3	43,9	47,7	-3,8
n-2	14,3	32,1	-17,8
n-1	-64,4	-14,2	-50,2
n	-37,6	-61,8	24,2

• Wielkości błędów:

Nazwa błędu ex post	Wartość błędu
ME	-0,25714
MAE	19,57376
RMSE	24,12877891
vp	93,8351828

PiS (2010/2011) - Sprawozdanie 5

4

---