Politechnika Śląska
Wydział AEiI
Laboratorium z fizyki
Absorpcja promieniowania γ
Grupa 4., sekcja 7.
Wioletta Bujak
Arkadiusz Mazur
Andrzej Zwierzchowski1. Wstęp teoretyczny.
Promieniowanie γ jest jednym z wysokoenergetycznych, elektromagnetycznych promieniowań jądrowych. Powstaje ono w trakcie przechodzenia jądra atomowego o wzbudzonym stanie energetycznym do stanu niższego. Różnica energii pomiędzy tymi poziomami zostaje wypromieniowana w postaci kwantu promieniowania elektromagnetycznego - fotonu γ Promieniowanie to oddziałuje z ośrodkiem, w którym się rozchodzi, czyli z elektronami, jądrami i polem elektrycznym jądra. Z oddziaływaniami tymi mamy do czynienia w zjawiskach:
- fotoelektrycznym;
- tworzenia par elektron-pozyton;
- zjawisku Comptona.
W celu zbadania oddziaływania promieniowania γ z materią najlepiej jest wykorzystać zjawisko Comptona, ponieważ w dwóch pozostałych zjawiskach oddziałujący foton γ zostaje całkowicie zaabsorbowany. W zjawisku fotoelektrycznym energia fotonu zostaje zużyta na jonizację fotonu i nadanie energii kinetycznej wybitemu elektronowi. Podczas tworzenia się par elektron-pozyton przy współdziałaniu jądra foton przekształca się w elektron i pozyton. Natomiast w zjawisku Comptona część energii fotonu γ zostaje przekazana elektronowi, z którym się zderza. Foton o niższym poziomie energii zostaje odchylony o pewien kąt od kierunku pierwotnego.
Jeśli na drodze wiązki promieniowania γ zostanie umieszczona płytka absorbenta, to jej natężenie zmaleje, ponieważ kwanty γ są usuwane z wiązki w skutek oddziaływania z absorbentem. Usuwanie zachodzi z określonym prawdopodobieństwem zależnym od energii fotonów wiązki i materiału absorbenta.
Oddziaływanie fotonów γ z materią można scharakteryzować za pomocą prawdopodobieństwa usunięcia z wiązki na jednostkę drogi przebytej w absorbencie. Własność:
n(x) = n0 * e -px
określa ilość n kwantów w wiązce w zależności od drogi x przebytej w absorbencie, gdzie:
n0 - początkowa ilość kwantów γ;
p - prawdopodobieństwo przypadające na jednostkę drogi w absorbencie.
Grubość absorbenta osłabiającego natężenie wiązki do połowy początkowej wartości nazywamy grubością połówkowego osłabienia i wynosi ona:
x1/2 = ln 2/p.
Ponieważ w konkretnym materiale wartość x1/2 zależy jednoznacznie od energii promieniowania γ, więc można jej użyć do wyznaczenia tej energii.
2. Wyniki pomiarów.
Po przeprowadzeniu doświadczenia otrzymaliśmy następujące wyniki:
średnia wartość tła:
(61+69+59+54+55)/5 ≈ 60 impulsów / min.
Grubość ołowiu [cm] |
Liczba impulsów na minutę [1/min] |
Liczba impulsów na minutę po odjęciu tła [1/min] |
0 |
2146 |
2086 |
0,51 |
1557 |
1497 |
1,04 |
1259 |
1199 |
1,524 |
933 |
873 |
2,038 |
669 |
609 |
3,064 |
401 |
341 |
4,078 |
230 |
170 |
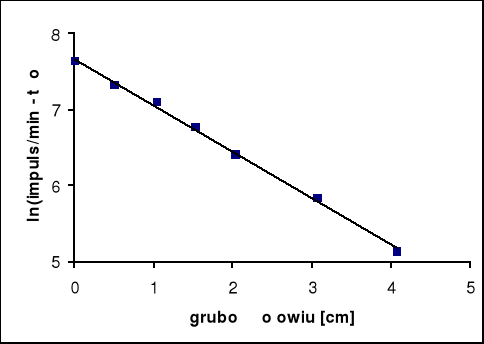
Od wyznaczonej szybkości zliczeń impulsów została odjęta wartość tła. Otrzymane wartości zostały po zlogarytmowaniu naniesione na wykres w zależności od grubości przysłony:
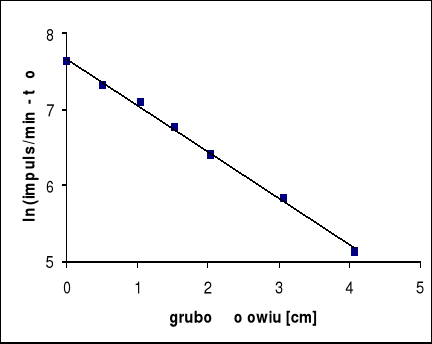
3. Obliczenia.
Równanie prostej regresji:
y = ax + b
gdzie :
a = -0,611 , cm]
b = 7,669 ,
Współczynnik kątowy a prostej regresji służy do obliczenia grubości połówkowego osłabienia d1/2:
przy czym błąd wynosi:
Podstawiając wartości liczbowe otrzymujemy:
d1/2 = 1,134 [ cm ]
d1/2 = 0,024 [ cm ]
Najczęściej wartość grubości połówkowego osłabienia wyraża się w jednostkach masowych:
dm = d1/2 * ρPb
Gęstość ołowiu wynosi: ρPb = 11,34 [ g/cm3 ]
Podstawiając wartości liczbowe otrzymujemy:
dm = 12,86 [ g/cm2 ]
dm = 0,27 [ g/cm2 ]
Korzystając z wykresu zależności grubości połówkowego osłabienia od energii promieniowania γ można odczytać średnią wartość energii tego promieniowania:
E = 1,41 [ MeV ]
Niestety, nie możemy wyznaczyć wartości błędu w MeV, ponieważ na dostępnym wykresie brakło skali.
4. Wnioski.
Ponieważ energia promieniowania γ izotopu 60Co mieści się w granicach 1,17 - 1,33 MeV, otrzymany wynik różni się od rzeczywistego o 5 - 17 %.
Dokładność wyników doświadczenia wzrosłaby przy wielokrotnym powtarzaniu pomiarów i uśrednieniu otrzymanych wartości dla konkretnej grubości przysłony. Wynika to z tego, że otrzymane przez nas wyniki pomiarów są tylko jednymi z możliwych, gdyż zjawisko to opisane jest przez rozkład Gaussa, a zwiększenie ilości pomiarów pozwala na uzyskanie bardziej prawdopodobnej liczby zliczanych impulsów.
Błąd wyznaczania grubości połówkowego osłabienia został obliczony przy użyciu metody różniczki zupełnej.
Wyszukiwarka
Podobne podstrony:
Kopia widma absorpcyjne, Księgozbiór, Studia, Fizyka, Biofizyka
Kopia absorpcjometr, Księgozbiór, Studia, Fizyka, Biofizyka
06 Badanie zaleznosci sily, Księgozbiór, Studia, Fizyka
metoda Bragga, Księgozbiór, Studia, Fizyka
Kopia cechowanie termopary, Księgozbiór, Studia, Fizyka, Biofizyka
Drgania har. -Aga, Księgozbiór, Studia, Fizyka
Wyznaczanie energii maksymalnej promieniowania beta, Księgozbiór, Studia, Fizyka
IS1, Księgozbiór, Studia, Fizyka
Analiza spr, Księgozbiór, Studia, Fizyka
LABFIZ08, Księgozbiór, Studia, Fizyka
bragg, Księgozbiór, Studia, Fizyka
Kopia hematokryt, Księgozbiór, Studia, Fizyka, Biofizyka
rezyst, Księgozbiór, Studia, Fizyka
więcej podobnych podstron