WYKŁAD 2
Własności funkcji ciągłych na przedziale domkniętym i ograniczonym:
1) funkcja f ciągła na <a,b> jest ograniczona na <a,b>
2)funkcja f ciągła na <a,b> jest na tym przedziale jednostajnie ciągła
3) funkcja f ciągła na <a,b> osiąga w nim swoje kresy: supremum i infemum, tzn. istnieją takie punkty x1,x2 Є<a,b> że
supxЄ<a,b> f(x)=f(x1), infxЄ<a,b>f(x)=f(x2)
4)jeżeli f jest ciągła na <a,b> oraz f(a)*f(b)<0 to istnieje taki punkt cЄ(a,b) że f(c)=0
5) własność Darboux: jeżeli funkcja f jest ciągła na przedziale I(niekoniecznie domkniętym) oraz przyjmuje w punktach x1,x2 Є I, x1<x2dwie różne wartości y1=f(x1), y2=f(x2) to f przyjmuje w przedziale < x1,x2 > wszystkie pośrednie wartości między y1a y2tzn.![]()
yo=f(x0)
Wniosek:
Wartości funkcji ciągłej na przedziale domkniętym <a,b> wypełnia przedział domknięty <infxЄ<a,b>f(x), sup xЄ<a,b>f(x)>.
6)jeżeli f jest funkcją różnowartościową wzajemnie jednoznaczną, ciągłą na przedziale <a,b> to funkcja odwrotna f-1 jest ciągła na przedziale <infxЄ<a,b>f(x), sup xЄ<a,b>f(x)>.
Uwaga:
Każda funkcja f jednostajnie ciągła na <a,b> (lub (a,b)) tzn. 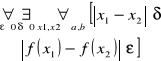
Jest ciągła na (a,b) oraz jednostajnie ciągła na końcach tego przedziału.
Rachunek różniczkowy funkcji rzeczywistej jednej zmiennej.
1)Pochodna funkcji rzeczywistej zmiennej rzeczywistej
Dana jest funkcja f: (a,b) o wartościach rzeczywistych. Niech x0Є(a,b).
Dla x1Є(a,b) przyrostem zmiennej niezależnej nazywamy różnicę ∆x= x1-x2, a przyrostem zmiennej zależnej nazywamy różnice ∆y=f(x1)-(x2).
Iloraz postaci: ![]()
przy x0≠0 to iloraz różnicowy funkcji f w x.
Jeżeli przy ∆x→0 istnieje granica właściwa lub niewłaściwa ilorazu różnicowego ![]()
to punktowi x0Є(a,b) można przyporządkować wyrażenie 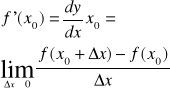
Zmieniając x0Є(a,b) uzyskujemy funkcje f'.
Def.
Funkcja f' gdzie ![]()
nazywamy pochodną funkcji f.
Def.
Pochodną lewostronną funkcji f nazywamy funkcją f'l przy czym ![]()
Pochodną prawostronną funkcji f nazywamy funkcją f'p przy czym ![]()
przykłady:
a) wykazać, że (xn)'=nxn-1 dla n=1,2.., określić zbiór xЄR dla których wzór ten zachodzi.
Dowód: oznaczamy przez ∆x przyrost zmiennej niezależnej, wtedy: 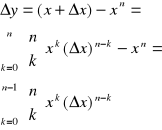
Przy ∆x≠0.
Stąd:
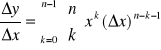
oraz
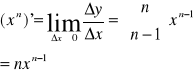
czyli (xn)'=nxn-1
powyższy wzór zachodzi przy n>1 dla każdego xЄR. Natomiast przy n=1 wzór ten ma miejsce gdy x≠0. ponadto widać, że ![]()
dla każdego xЄR.
b) zbadać pochodną funkcji f(x)=|x|, xЄR w punkcie x0=0 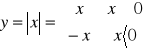
pochodne jednostronne funkcji f w x0 wynoszą 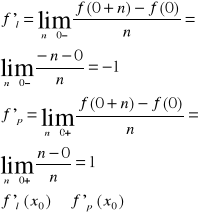
oznacza to, że w x0=0 nie istnieje pochodna funkcji f(x)=|x| mimo,że funkcja ta jest ciągła w x0=0.
Twierdzenie 1.
Jeżeli funkcja f określona na przedziale (a,b) posiada skończoną pochodną w x0=(a,b), to funkcja jest ciągła w x0.
Dowód:
Ponieważ istnieje skończona granica:

więc
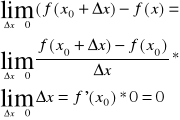
czyli
![]()
zatem f jest ciągła w x0.
Uwaga:
Przykład funkcji f(x)=|x|, xЄR świadczy o tym że twierdzenie odwrotne nie zachodzi.
Twierdzenie 2.
Jeżeli funkcje f,g posiadają skończone pochodne w x0Є(a,b) to:
a) kombinacja liniowa: α*f+β*g, gdzie α,β to stałe rzeczywiste, posiada skończoną pochodną w x0 oraz (α*f+β*g)'(x0)=
α*f'(x0)+β*g'(x0).
b) iloczyn f*g posiada skończoną granicę w x0 oraz
(f*g)' (x0)= f'(x0)*g(x0)+f(x0)*g'(x0).
c) przy dodatkowym założeniu g(x0)≠0 istnieje skończona pochodna ilorazu f/g
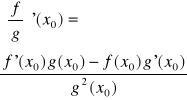
dowód a: we własnym zakresie
dowód b: 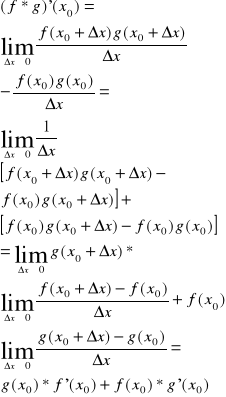
(
gdyż g jest ciągła w x0.
Dowód c:
ponieważ g(x0)≠0 oraz g jest ciągła w w x0 więc dla dostatecznie bliskich zera ∆x, ∆x≠0 ,mamy g(x0+∆x0)≠0.
(f/g)'(x0)=
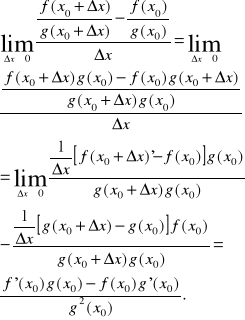
Twierdzenie 3.
Jeżeli:
a) funkcja g jest ciągła na <a,b> oraz istnieje skończona pochodna g'(x0) dla
x0Є(a,b)
b) funkcja f jest określona na przedziale <c,d> oraz posiada skończoną pochodną w punkcie g(x0).
To pochodna superpozycji h=f*g=f(g) jest równa h'(x0)= (f*g)'(x0)=f'(g (x0))* g'(x0)
Dowód:
Ponieważ istnieje skończona pochodna g'(x0) oraz f'(x0) więc przy y0= g(x0) można napisać: g(x0+∆x0)-g(x0)= ∆x(g'(x0)+u(x0,∆x))
f(y0+∆y)-f(y0)=∆y(f'(y0)+v(y0,∆y0)
gdzie:
u(x0,∆x)→0 przy ∆x→0
v(y0,∆y0)→0 przy ∆y→0
Zatem:
h(x0+∆x0)-h(x0)= f|g(x0+∆x0)|-f|g(x0)|=
f|g (x0)+∆y)|-f|g(x0)|=
f|(y0+∆y0|-f(y0)= ∆y(f'(y0)+v(y0,∆y0)=
|g(x0+∆x0)-g(x0)|*(f'(x0)+v(y0,∆y0)=
∆x(g(x0)+ u(x0,∆x0).
Twierdzenie 4.
Jeżeli funkcja f jest ciągła i ściśle monotoniczna na <a,b> oraz istnieje skończona pochodna f'(x0)≠0 w punkcie x0Є(a,b) to funkcja odwrotna f -1 posiada pochodną w punkcie y0=f(x0) oraz ![]()
Pochodne funkcji elementarnych:
a) f(x)=sinx
![]()
ponieważ:
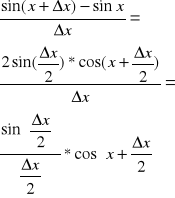
więc przy ∆x→0 otrzymujemy f(x)=(sinx)'=cosx, gdyż cos jest unkcją ciągłą f(x)= cosx.
Korzystając z twierdzenia o pochodnej funkcji złożonej, mamy:
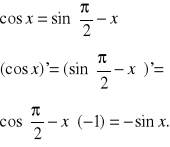
f(x)=tgx

f(x)=ctg
![]()
b) f(x)=arcsinx, f -1=siny, ![]()
, x'(y)= cosy
Na mocy tw.4 mamy:
y'(x)=1/cosy ,ponieważ
![]()
(znak `+', bo ![]()
) więc
![]()
dla xЄ(-1,1)
podobnie otrzymujemy
![]()
dla xЄ(-1,1)
f(x)=arctgx
Funkcją odwrotną do niej jest funkcja x=tgy ![]()
, ponieważ![]()
więc:

ponadto otrzymujemy
![]()
c)f(x)= logax a>0 ,a≠1, x>0
poneważ:

więc
![]()
w szczególności (lnx)'=1/x
d) f(x)=ax, a>0
ponieważ funkcją odwrotną do y= ax jest x= logay więc 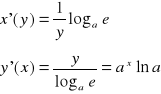
w szczególności (ex)'= ex
e)![]()
1˚ wiadomo, że dla funkcji potęgowej xn , nЄN:
![]()
f'(x0)=1 dla n=1
2˚dla nЄN mamy przy x≠0
![]()
3˚Jeżeli x=1/n n-liczba całkowita różna od zera, to funkcja ![]()
jest odwrotna do funkcji xn a więc przyjmuje ![]()
mamy x= xn oraz 
4˚dla ![]()
, gdzie m to liczba całkowita nЄN mamy 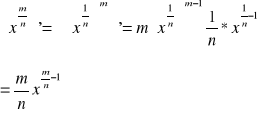
5˚ jeżeli ![]()
to mamy przy x>0 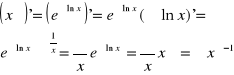
Podsumowanie:
![]()
Interpretacja geometryczna i mechaniczna pochodnej
a) Niech funkcja f będzie określona na przedziale (a,b) oraz niech f posiada skończoną pochodną f'(x0) w x0Є(a,b).
Równanie prostej przechodzącej przez punkty P0 i P1:
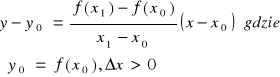
lub
![]()
przy ∆x→0 sieczna P0 P1dąży do położenia granicznego którym jest styczna do krzywej y=f(x) w punkcie P0 (podobnie jest gdy ∆x<0).
Współczynnik kierunkowy siecznej
![]()
dąży do pochodnej w x0.
Zatem:
Pochodna f'(x0) jest równa tangesowi kąta, który tworzy styczne do krzywej y=(x) z osia OX.
Zatem, jeżeli funkcja f posiada w x0Є(a,b) skończoną pochodną f'(x0) to równanie stycznej do krzywej y=f(x) w x0 ma postać:
y- y0= f'(x0)(x-x0).
Jeżeli funkcja f ma w x0 pochodną równą +∞ lub -∞ to równanie stycznej ma postać x= x0 .
b) Niech dane ciało materialne porusza się po osi liczbowej OX. W chwili t ciało znajduje się w punkcie M o współrzędnej s=f(t). W chwili początkowej t0 ciało znajduje się w punkcie M0 o współrzędnej s0= f(t0).Po upływ czasu ∆t ciało znajduje się w punkcie M1 o współrzędnej s1= f(t0+∆t).
Oznaczamy ∆s =s1-s0.Granicę ![]()
nazywam prędkością ciała w chwili t0 i oznaczamy przez v(t0), czyli 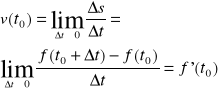
Przy założeniu że f'(t0) jest skończona.
c) Badamy reakcje syntezy substancji C, powstającej z substancji A i B. Ilość y substancji C zależy w następujący sposób od czasu t trwania reakcji y=f(t).
W chwili t0, ilość substancji C wynosi y0=f(t0) po upływie czasu ∆t ilość substancji C jest równa y1= f(t0+∆t).
Prędkość substancji w chwili t0 wynosi
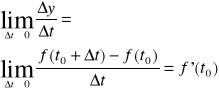
(przy założeniu istnienia skończonej pochodnej).
Pochodna funkcji przedstawiona parametrycznie:
Dane są funkcje:
![]()
określone i ciągłe względem parametru t, ![]()
podające związek imiennych x i y przy pomocy t.
Zakładamy, że :
φ jest ściśle monotoniczna
istnieje skończona pochodna φ'(t0)≠0 i ψ'(t0) dla
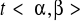
Zatem istnieje funkcja odwrotna φ-1 : t = φ-1 (x) ciągła i ściśle monotoniczna.
Funkcja złożona: ![]()
Jest ciągła, ponieważ:
![]()
więc na podstawie twierdzenia o pochodnej funkcji złożonej otrzymujemy
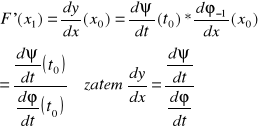
Wyszukiwarka
Podobne podstrony:
Wykład Chemia kwantowa 11
Wykład 9 CHEMIA ORGANICZNA
Zakres materiału obowiązujący na II kolokwium wykładowe, Chemia ogólna i nieorganiczna, giełdy
WYKŁAD 1 chemia, Chemia
wykłady chemia sem 1
Rzeczy których nie ma u piegusa wykład chemia( 02 2014
WYKŁAD chemia gips
Chemia wykłady, Chemia wykłady-mini, → ORBITALE ATOMOWE WODORU
WYKŁADY, chemia zywnosci w2-9, WYKŁAD 2
WYKŁADY, CHEMIA ZYWNOSCI nasze wyklady
WYKŁADY, chemia zywnosci w2-9, WYKŁAD 2
WYKŁADY, CHEMIA ZYWNOSCI nasze wyklady
Wykład Chemia kwantowa 2
chemia egzaminy!!, Studia Budownictwo UZ, 1 semestr, Chemia budowlana, Wykłady, chemia
więcej podobnych podstron