1998/99	LABORATORIUM Z FIZYKI
Ćwiczenie nr 72	Zjawisko Halla
ELEKTRONIKA gr. 1.1	Paweł Wojdaszko
Data wykonania:		Data	Ocena	Podpis
1999.05.16	T
	S

Zasada pomiaru:

Zjawisko Halla polega na powstawaniu pola elektrycznego E w płytce półprzewodnika, przez którą płynie prąd, umieszczonej w polu magnetycznym B:

Na powierzchniach bocznych płytki powstaje nadmiarowy ładunek - na jednej dodatni, na drugiej ujemny, w wyniku czego powstaje dodatkowe pole elektryczne o natężeniu:

działające na elektrony siłą
skierowaną przeciwnie do siły Lorentza.

Po ustaleniu się równowagi, FE = FL:

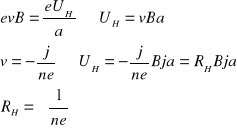
v -średnia prędkość elektronów

j - gęstość prądu w płytce

n - koncentracja elektronów

Stałą Halla RH (mającą znak ujemny w przypadku przewodnictwa n, lub ujemny dla przewodnictwa p), można wyznaczyć doświadczalnie ze wzoru:

b - grubość płytki

Przy znanej stałej Halla można obliczyć koncentrację elektronów swobodnych w metalu lub elektronów przewodnictwa w półprzewodniku zdegenerowanym oraz ich ruchliwość - ruchliwość holowską:

- opór właściwy materiału

Układ pomiarowy:

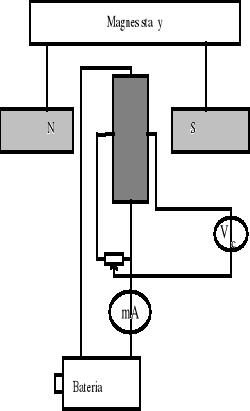
Ocena dokładności pojedynczych pomiarów:

woltomierz cyfrowy:

- dokładność 0,001V

- błąd maksymalny: ΔU = ±0,5 % + 1 znak

miliamperomierz:

- zakres: 15 mA

- podziałek: 60, 1 podziałka = 0,25 mA

• klasa: 0,5

- błąd maksymalny wyznaczany ze wzoru:

= 0,15 [mA]

Ze względu na nieliniowe zachowanie potencjometru regulującego prąd, szczególnie
przy wyższych wartościach trudne było dokładne ustawienie zadanych parametrów, dlatego też błąd pomiaru natężenia wynika również z przyczyn mechanicznych.

Tabele wyników:

a) parametry próbki i warunki pomiarów efektu Halla:

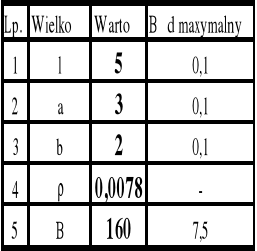
l - długość próbki

a - szerokość próbki

b - grubość próbki

- oporność właściwa

przenikalność magnetyczna 1

materiał - monokryształ Ge

typ przewodnictwa - n

Lp.	I	-UH	UH	UHśr	UHśr*I
		[mA]	[mV]	[mV]	[mV]	[mV][mA]
1.	2,00 ± 0,15	0,16 ± 0,001	0,17 ± 0,001	0,16 ± 0,002	0,33
2.	3,00 ± 0,15	0,24 ± 0,001	0,21 ± 0,001	0,22 ± 0,003	0,67
3.	4,00 ± 0,15	0,31 ± 0,002	0,29 ± 0,002	0,30 ± 0,004	1,20
4.	5,00 ± 0,15	0,39 ± 0,002	0,36 ± 0,002	0,37 ± 0,004	1,87
5.	6,00 ± 0,15	0,48 ± 0,003	0,44 ± 0,003	0,46 ± 0,006	2,76
6.	7,00 ± 0,15	0,54 ± 0,003	0,55 ± 0,003	0,54 ± 0,006	3,81
7.	8,00 ± 0,15	0,60 ± 0,003	0,60 ± 0,003	0,60 ± 0,006	4,80
8.	9,00 ± 0,15	0,74 ± 0,004	0,66 ± 0,004	0,70 ± 0,008	6,30
9.	10,00 ± 0,15	0,87 ± 0,005	0,74 ± 0,004	0,80 ± 0,009	8,05
10.	11,00 ± 0,15	0,90 ± 0,005	0,80 ± 0,004	0,85 ± 0,009	9,35
11.	12,00 ± 0,15	0,93 ± 0,005	0,91 ± 0,005	0,92 ± 0,010	11,04
12.	13,00 ± 0,15	1,04 ± 0,006	1,04 ± 0,006	1,04 ± 0,012	13,52
13.	14,00 ± 0,15	1,16 ± 0,006	1,11 ± 0,006	1,13 ± 0,012	15,89
14.	15,00 ± 0,15	1,13 ± 0,006	1,28 ± 0,007	1,20 ± 0,013	18,07
Δ	0,15	0,004	0,004	-	-
ε	-	-	-	9,33	97,68

Lp.	I^2	UHśr*ΔI	I*ΔUHśr	I*ΔI	UH (teor.)
		[mA^2]	[mV][mA]	[mV][mA]	[mA^2]	[mV]
1.	4	0,03	0,01	0,30	0,16
2.	9	0,04	0,01	0,45	0,24
3.	16	0,05	0,02	0,60	0,32
4.	25	0,06	0,02	0,75	0,40
5.	36	0,07	0,04	0,90	0,48
6.	49	0,09	0,05	1,05	0,56
7.	64	0,10	0,05	1,20	0,64
8.	81	0,11	0,08	1,35	0,72
9.	100	0,13	0,09	1,50	0,80
10.	121	0,13	0,10	1,65	0,88
11.	144	0,14	0,12	1,80	0,96
12.	169	0,16	0,16	1,95	1,04
13.	196	0,18	0,17	2,10	1,12
14.	225	0,19	0,20	2,25	1,20
ε	1239	1,48	1,12	17,85	-

Wykres:

Przykładowe obliczenia:

1. współczynnik kierunkowy prostej:

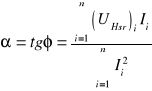
= 97,68 / 1239 = 0,08

= 4,57

2. stała Halla:

RH= 0,08*2*10-6/(160*10-3)= 0,001*10-3 m3/C

3. koncentracja elektronów:

n = 1/(0,001*10-3*1,602*10-19) = 6,243*1024/m3 = 6,243*1018/cm3

4. ruchliwość nośników:

H= 0,001*10-3/(7,8*10-3) = 0,000129 m²/s*v

Rachunek błędów:

Błędy wynikające z zastosowanych przyrządów pomiarowych zostały podane w punkcie o dokładności pojedyńczych pomiarów

U = ± 0,5 % V

I =

Wzór na błąd pomiaru stałej :

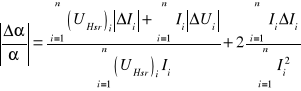
można uprościć do postaci:

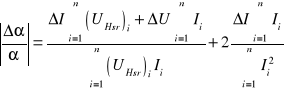
gdyż wszystkie pomiary zostały wykonane przy tych samych zakresach przyrządów:

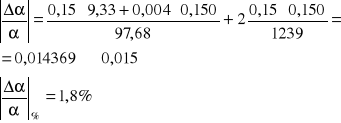
= 0,0012 0,002

Stąd błąd pomiaru stałej Halla obliczony metodą różniczki logarytmicznej wynosi:

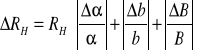
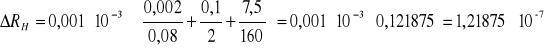
m³/c

RH= 1,21875*10-71,3*10-7 m³/c

Zważywszy na warunki pomiarów, a zwłaszcza rozregulowany potencjometr do ustawiania prądu, błąd rzędu 11% wydaje się być jeszcze zadawalający.

Zestawienie wyników:

RH = (1,00 0,13) * 10-6 m3/C

2 Olszewski. Opracowanie doświadczenia 1997/98.

---