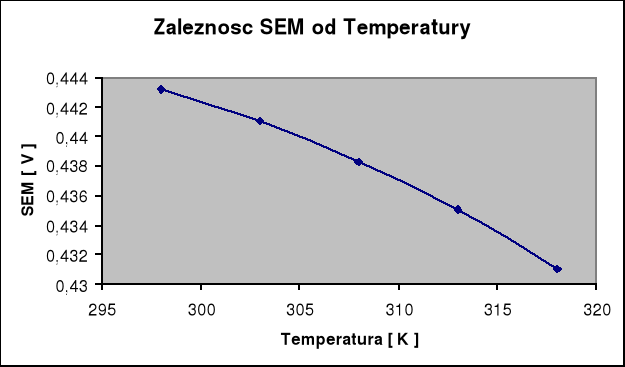
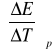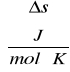ZESTAWIENIE WYNIKÓW
TEMPERATURA [ C] |
TEMPERATURA [ K ] |
SEM |
25 |
298 |
0,4432 |
30 |
303 |
0,4410 |
35 |
308 |
0,4383 |
40 |
313 |
0,4350 |
45 |
318 |
0,4310 |
1. W ogniwie chemicznym zachodzą nastepujące procesy:
na anodzie: 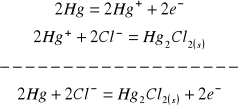
na katodzie: ![]()
co sumarycznie daje: ![]()
2. Używane w pomiarach ogniwo można przedstawić schematycznie w następujący sposób:
(-) ![]()
(+)
3. Równanie Nersta na SEM badanego ogniwa:
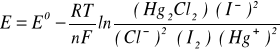
[V]
Ponieważ aktywność ciał stałych jest równa 1, więc (I2)=1 i (Hg2Cl2)=1. Wartość aktywności jonów Hg+ pomijamy ze względu na bardzo małe stężenie.
Stąd:
![]()
[V]
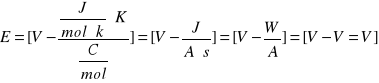
gdzie:
E- siła elektromotorczna [V]
E0 - normalna siła elektromotoryczna [v]
R - stała gazowa - 8,314 [J/mol.K]
T - temperatura bezwzględna [K]
n - liczba elektronów biorących udział w reakcji
F - stała Faradaya - 96485,3 C/mol
4. Dane literaturowe na temat potencjałów normalnych elektrod używanych w doświadczeniach:
Elektroda |
Reakcja elektrodowa |
Potencjał E0 [V] |
I-/I2,Pt |
I2+2e-= 2I- |
+0,5360 |
Cl-/Hg2Cl2,Hg |
2Hg ++2 Cl-= Hg2Cl2 |
+0,2680 |
5. Obliczenia normalnej siły elektromotorycznej ogniwa ( dla aktywności reagentów równych jedności) - ΔE0:
![]()
[V]
gdzie: E01 - potencjał normalny elektrody dodatniej [V]
E02 - potencjał normalny elektrody ujemnej [V]
ΔE0=0,5360-0,2680=0,2680 [V]
6. Obliczenie stosunku aktywności jonów I-/Cl- w ogniwie na podstawie zmierzonej wartości SEM ogniwa (napięcia ogniwa w warunkach bezprądowych) w warunkach standardowych i obliczonej wartości normalnej siły elektromotorycznej ogniwa:
Stosunek aktywności jonów I-/Cl- wyznaczamy z równania Nersta na SEM badanego ogniwa
![]()
po przekształceniu:
![]()
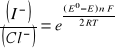
otrzymujemy:

7. Wartość współczynnika temperaturowego.

![]()
8. Z równania Gibbsa-Helmholtza obliczamy efekt cieplny ΔH, zmianę entalpii swobodnej ΔG oraz zmianę entropii ΔS w określonych warunkach temperatury, ciśnienia i stężenia reagentów. Obliczenia przeprowadzamy dla temperatury końcowej (najwyższej), w której badaliśmy dane ogniwo SEM - 450C:
Obliczamy entalpię swobodną :
![]()
= z .F .E
z = 2
F = 96485,31 [C/mol]
- dla 25,1 0C E = 0,4432 [V]
![]()
= - 2 * 96485,31 * 0,4432 = -85524,5![]()
- dla 30,1 0C E = 0,4410 [V]
![]()
= -85100,0![]()
- dla 35 0C E = 0,4383 [V]
![]()
= -84579,0![]()
- dla 40,05 0C E = 0,4350 [V]
![]()
= -83942,2![]()
- dla 45 0C E = 0,4310 [V]
![]()
= -83170,3![]()
![]()
=![]()
b) Obliczamy entropię:
![]()
= z .F .![]()
z = 2
F = 96485,31 [C/mol]
dla 25,1 0C
![]()
= 0
dla 30,1 0C ΔT = 5K ΔE=2,22*10-3
![]()
= 85,7 [J/mol *K]
dla 35 0C ΔT =4,9K ΔE=2,7*10-3
![]()
= 106,3[J/mol * K]
dla 40,05 0C ΔT = 5,05K ΔE=3,3*10-3
![]()
= 126,1 [J/mol * K]
dla 45 0C ΔT = 4,95K ΔE=4*10-3
![]()
=155,9 [J/mol * K]
ΔS= ![]()
Obliczamy entalpię :
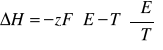
![]()
T = 25,1 0C
![]()
0
T = 30,1 0C
![]()
-82524,33
T = 35 0C
![]()
-80862,1
T = 40,05 0C
![]()
-78895,8
T = 45 0C
![]()
-76158,7
ΔH = ![]()
9. Obliczamy zależność SEM od temperatury :
![]()
z = 2
F = 96485,31
- dla T=25,1 0C ![]()
= 0
![]()
= 0
- dla T=30,1 0C ![]()
= 85,7
![]()
= 4,4* ![]()
- dla T=35 0C ![]()
=106,3
![]()
= 5,5 * ![]()
- dla T=40,05 0C ![]()
= 126,1
![]()
= 6,5 * ![]()
- dla T=45 0C ![]()
= 155,5
![]()
= 8,1 * ![]()
OPRACOWANIE WYNIKÓW:
TABELA POMIAROWA
T [°C] |
SEM [V] |
|
|
|
|
25,1 |
0,4432 |
- |
-85524,5 |
- |
- |
30,1 |
0,4410 |
-0,00044 |
-85100,0 |
84,9 |
-82524,3 |
35 |
0,4383 |
-0,00054 |
-84579,0 |
104,2 |
-80862,1 |
40,05 |
0,4350 |
-0,00066 |
-83942,2 |
127,3 |
-78895,8 |
45 |
0,4310 |
-0,0008 |
-83170,3 |
154,3 |
-76158,7 |
1
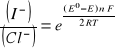
Wyszukiwarka
Podobne podstrony:
0 611 235 708 GBH 7 DE
0 611 222 703 GBH 4 DSC
611 Orędzie Żywego Płomienia Już za moment zatrzymam czas
0 611 228 703 GBH 2 24 DSR
0 611 238 703 GBH 2 24 DFR
0 611 218 703 GBH 2 24 DSR
611
611
611
44 611 624 Behaviour of Two New Steels Regarding Dimensional Changes
harm szkolen 611 po kl leg
avt 611 Alarm termiczny
611
610 611
611
611
611
2015 OR ćwid(611
więcej podobnych podstron