SPRAWOZDANIE Z LABORATORIUM Z FIZYKI

ĆWICZENIE NR. 8

BADANIE ZALEŻNOŚCI TEMPERATUROWEJ PRZEWODNICTWA ELEKTRYCZNEGO METALI I PÓŁPRZEWODNIKÓW.

SEKCJA VI T - 13:

Marcin Cholewa

PRZEBIEG ĆWICZENIA:

1. Ustalamy natężenie I = 1, 2 [mA] prądu płynącego przez próbkę metalową.

2. Włączamy termostat i nastawiamy na nim żądaną temperaturę pomiarową.

3. Wyznaczamy dokładną temperaturę danych próbek kierując się wskazaniami miernika temperatury podłączonego do termopary.

4. Mierzymy spadek napięcia U przy przepływie prądu elektrycznego przez próbkę metalową.

5. Mierzymy rezystancję próbki półprzewodnikowej.

6. Pomiary opisane w p. 3, 4, 5 przeprowadzamy w zakresie temperatur od 25⁰ C do 95⁰ C co 5⁰ C.

7. Notujemy klasy dokładności i zakresy pomiarowe użytych mierników.

TEMPERATURA [^0 C]	U [mV]	R [kΩ]
22, 1	121, 2	0, 701
25	122, 7	0, 770
30	123, 9	0, 716
35	125, 4	0, 650
40	126, 8	0, 582
45	128, 3	0, 521
50	129, 8	0, 461
55	131, 3	0, 404
60	133, 0	0, 354
65	134, 6	0, 307
70	136, 6	0, 267
75	138, 0	0, 232
80	139, 6	0, 203
85	141, 4	0, 176
90	143, 1	0, 153
95	144, 9	0, 133

KLASY DOKŁADNOŚCI I ZAKRESY POMIAROWE UŻYTYCH MIERNIKÓW:

1. AMPEROMIERZ

2. OMOMIERZ

3. WOLTOMIERZ

4. TERMOMETR

	ZAKRES	KLASA DOKŁ.	Δ
AMPEROMIERZ	5 [mA]	1,5 [mA]	0,075 [mA]
OMOMIERZ	2 [kΩ]	0,05 [kΩ]	0,001 [kΩ]
WOLTOMIERZ	200 [mV]	0,05 [mV]	0,1 [mV]
TERMOMETR	200 [^0C]	0,05 [^0C]	0,1 [^0C]

KORZYSTAJĄC Z PRAWA OHMA WYZNACZAMY REZYSTANCJĘ PRÓBKI METALOWEJ.

U [V]	J [A]	R [Ω]	ΔR [Ω]
0,1212	0,0012	101, 00	6, 40
0,1227	0,0012	102, 25	6, 47
0,1239	0,0012	103, 25	6, 54
0,1254	0,0012	104, 50	6, 61
0,1268	0,0012	105, 67	6, 69
0,1283	0,0012	106, 92	6, 77
0,1298	0,0012	108, 17	6, 84
0,1313	0,0012	109, 42	6, 92
0,1330	0,0012	110, 83	7, 01
0,1346	0,0012	112, 17	7, 09
0,1366	0,0012	113, 83	7, 20
0,1380	0,0012	115, 00	7, 27
0,1396	0,0012	116, 33	7, 35
0,1414	0,0012	117, 83	7, 45
0,1431	0,0012	119, 25	7, 54
0,1449	0,0012	120, 75	7, 63

ZA POMOCĄ RÓŻNICZKI ZUPEŁNEJ OBLICZAMY NIEPEWNOŚCI REZYSTANCJI:

ΔU = 1⋅10^-3 [V]

ΔJ =

DANE DO WYKRESU DLA PRÓBKI METALOWEJ:

T[⁰C] = T[⁰K] - 273

R [Ω]	T [^0K]
102,25	298
103,25	303
104,50	308
105,67	313
106,92	318
108,17	323
109,42	328
110,83	333
112,17	338
113,83	343
115,00	348
116,33	353
117,83	358
119,25	363
120,75	368

METODĄ NAJMNIEJSZYCH KWADRATÓW WYZNACZAMY PARAMETRY KIEUNKOWE PROSTEJ APROKSYMUJĄCEJ ZALEŻNOŚĆ REZYSTANCJI PRÓBKI METALOWEJ OD TEMPERATURY:

Dla n = 15

[K]

[Ω]

[KΩ]

[K²]

[K²]

[Ω²]

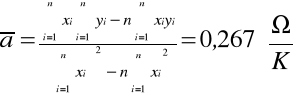
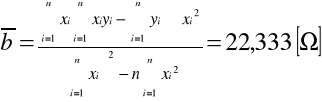
KORZYSTAJĄC Z WYZNACZONYCH PARAMETRÓW PROSTEJ APROKSYMUJĄCEJ R = aT + b ORAZ KORZYSTAJĄC Z NIŻEJ PODANEGO WZORU WYZNACZAMY WARTOŚĆ PARAMETRU α DANEJ PRÓBKI:

gdzie T₀ = 0 [⁰C] =273 [⁰K] a więc R₀ = 273a + b

natomiast

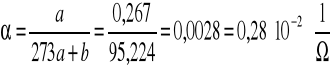
METODĄ RÓŻNICZKI ZUPEŁNEJ OBLICZAMY NIEPEWNOŚĆ TEGO WYNIKU:

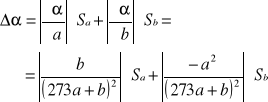
DANE DO WYKRESU PRÓBKI PÓŁPRZEWODNIKOWEJ:

R [Ω]	T [^0 K]
770	298
716	303
650	308
582	313
521	318
461	323
404	328
354	333
307	338
267	343
232	348
203	353
176	358
153	363
133	368

DLA PRÓBKI PÓŁPRZEWODNIKOWEJ SPORZĄDZAMY WYKRES ln R JAKO FUNKCJI ODWROTNOŚCI TEMPWRATURY 1/T:

DANE DO WYKRESU:

ln R	1/T
6,646391	0,003356
6,57368	0,0033
6,476972	0,003247
6,36647	0,003195
6,25575	0,003145
6,133398	0,003096
6,001415	0,003049
5,869297	0,003003
5,726848	0,002959
5,587249	0,002915
5,446737	0,002874
5,313206	0,002833
5,170484	0,002793
5,030438	0,002755
4,890349	0,002717

METODĄ NAJMNIEJSZYCH KWADRATÓW WYZNACZAMY PARAMETRY KIEUNKOWE PROSTEJ APROKSYMUJĄCEJ ZALEŻNOŚĆ REZYSTANCJI PRÓBKI PÓŁPRZEWODNIKOWEJ OD TEMPERATURY:

Dla n = 15

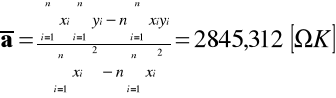
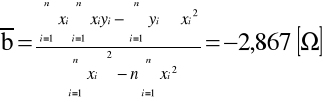
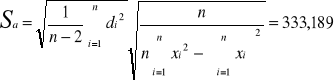
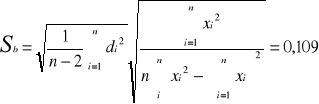
KORAYSTAJĄC Z WYZNACZONYCH PARAMETRÓW PROSTEJ APROKSYMUJĄCEJ ln R = 1/T ORAZ Z NIŻEJ PODANEGO WZORU WYZNACZAMY WARTOŚĆ ENERGII AKTYWACJI BADANEGO PÓŁPRZEWODNIKA.

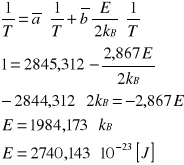
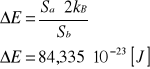
Dokładność wykonanych pomiarów uwarunkowana była dokładnością dysponowanego przez nas sprzętu. Błędy jakie mogą wystąpić są spowodowane niedokładnością odczytu z przyrządów mierniczych.

1

1

---