CYFROWE PRZETWARZANIE SYGNAŁ*W ELEKTRYCZNYCH

1. Cel ćwiczenia

Celem ćwiczenia jest poznanie zasad cyfrowego przetwarzania sygnałów oraz zalet i wad tego sposobu przetwarzania

3.1. Pomiary harmonicznych sygnału okresowego

Opis użytych przyrządów i programów

- komputer PC: procesor Pentium MMX, częstotliwość zegara 166MHz, pamięć RAM 32 MB, system operacyjny Windows XP

- program AH_CPSE opracowany w Zakładzie Metrologii Elektrycznej PŁ

Pomiary w przypadku, gdy znana jest wartość częstotliwości podstawowej harmonicznej

Badanie wpływu liczby próbek na parametry widma sygnału

Zwiększenie liczby próbek M wpływa na parametry widma korzystnie, gdyż powoduje

• wzrost gęstości prążków w widmie,

• wzrost liczby prążków N,

• wzrost szerokości widma f_g.

Badanie wpływu częstotliwości próbkowania na parametry widma sygnału

Zwiększenie częstotliwości próbkowania powoduje

• zwiększenie rozdzielczości widma f_W, co jest niekorzystne,

• zwiększenie f_g, co jest korzystne, oraz

• nie wpływa na N.

Powyższe wyniki badań są zgodne ze wzorami (wybrać wzory zawierające tylko M i f_S­):

Wnioski:

1. Jeżeli chcemy podwoić gęstość widma (zmniejszyć f_W 2-krotnie) bez zmniejszenia szerokości widma, to musimy 2 -krotnie  zwiększyć M i pozostawić bez zmian f_S.

2. Jeżeli chcemy podwoić szerokość widma bez zmniejszenia gęstości, to musimy 2 -krotnie zwiększyć f_S i po­zostawić bez zmian M.

Badanie wpływu niedokładnego nastawienia częstotliwości próbkowania na wyniki analizy harmonicznych

Obliczenia dla sygnału o liczbie harmonicznych n_max = 7

Liczba składowych widma powinna wynosić co najmniej

2nmax+1=15

Minimalna liczba próbek w oknie pomia­rowym wynosi

15

W celu zastosowania FFT wybieramy liczbę próbek

16

Obliczamy częstotliwość próbkowania i jej wartość po zwiększeniu o 1%

800
808

Zwiększamy liczbę próbek do M' = 16 i obliczamy maksymalną liczbę okresów

1

Odpowiada jej nowa częstotliwość próbkowania (zwiększona o 1%)

War­tość skuteczną sygnału obliczamy ze wzoru

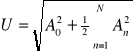
Wyniki pomiarów Tabela 3a

Sygnał - fala poliharmoniczna: n_max = 7, A₀ = 1 V, A₁ = 10 V, f₁ = 50 Hz, A_nmax = 4,03 V, f_nmax = 353,5Hz

Lp.		M		fS		A1p		f1p		A2p		f2p		A5p		f5p		Anmaxp		fnmaxp		Up
_		_		Hz		V		Hz		V		Hz		V		Hz		V		Hz		V
1.		16		800		10		50		9		100		6		250		4		350		14,195
2.		16		808		10,19		50,5		8,77		101		5,02		252,5		4,03		353,5		14,239
3.		16		792		9,80		49,5		9,22		99		6,90		247,5		3,83		346,5		14,148

Wyniki obliczeń błędów względnych pomiarów Tabela 3b

Lp.	δA1p	δf1p	δA2p	δf2p	δA5p	δf5p	δAnmaxp	δfnmaxp	δUp
_	%	%	%	%	%V	%	%	%	%
2.	1,9	1	-2,5	1	-16,3	1	0,7	1	0,3
3.	-2	-1	2,4	-1	15	-1	-4,2	-1	-0,3

Przykłady obliczeń

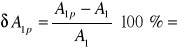
1,9%

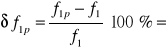
1%

0,3%

Wnioski:

1. W celu wykonania dokładnej analizy harmonicznych musimy znać częstotliwość pierwszej harmonicznej i numer najwyższej harmonicznej badanego sygnału.

2. Przy minimalnej liczbie próbek 1-procentowa odchyłka częstotliwości próbkowania od wartości prawidłowej powoduje większy błąd względny pomiaru amplitud harmonicznych.

3. Przy minimalnej liczbie próbek 1-procentowa odchyłka częstotliwości próbkowania od wartości prawidłowej powoduje taki sam błąd względny pomiaru częstotliwości harmonicznych.

Badanie wpływu niestabilności częstotliwości sygnału f₁ na wyniki analizy harmonicznych

Wyniki pomiarów Tabela 4a

Sygnał - fala poliharmoniczna: n_max = 9, A₀ = 1 V, A₁ = 10 V, A_nmax = 2 V, M = 32, f_S  =1600 Hz

Lp.	f1	A1p	f1p	A2p	f2p	A5p	f5p	Anmaxp	fnmaxp	Up
_	Hz	V	Hz	V	Hz	V	Hz	V	Hz	V
1.	49.5	10.209	50	8,75	100	5,05	250	0,048	750	13,959

Wyniki obliczeń błędów względnych pomiarów Tabela 4b

Lp.	δA1p	δf1p	δA2p	δf2p	δA5p	δf5p	δAnmaxp	δfnmaxp	δUp
_	%	%	%	%	%	%	%	%	%
1.	2	1	2,2	1	15,8	1	2,3	1	1,6

Wniosek

Odchyłka 1-procentowa częstotliwości badanego sygnału prawie ta­kie sa­me błędy w analizie harmonicznych, co 1-procentowa odchyłka częstotliwości próbkowania.

Badanie skutków niespełnienia przez liczbę próbek warunku M = 2^c

Nastawiamy liczbę próbek M = 96 i częstotliwość próbkowania f_S = 6400 Hz.

Wyniki pomiarów Tabela 5a

Sygnał - fala poliharmoniczna: n_max = 9, A₀ = 1 V, A₁ = 10 V, f₁ = 50 Hz, A_nmax = 2 V, f_nmax = 450 Hz

Lp.

M

Mrz

fS

A1p

f1p

A2p

f2p

A5p

f5p

Anmaxp

fnmaxp

Up

_

_

_

Hz

V

Hz

V

Hz

V

Hz

V

Hz

V

1.

96

128

6400

9,001

50

8,1524

100

6,6000

250

0,1300

3150

11,392

Wyniki obliczeń błędów względnych pomiarów Tabela 5b

Lp.	δA1p	δf1p	δA2p	δf2p	δA5p	δf5p	δAnmaxp	δfnmaxp	δUp
_	%	%	%	%	%	%	%	%	%
1.	-10	0	-5,3	0	10	0	3,2	0	24,6

Wniosek

Jeżeli liczba próbek nie spełnia warunku M = 2^c, to dużymi błędami obarczone są pomiary amplitud harmonicznych /i wartości skutecznej sygnału.

3.2. Badanie zjawiska nakładania się składowych widma

Doświadczalna weryfikacja wzoru na częstotliwość odbitej składowej widma

Wyniki pomiarów Tabela 7

Sygnał - 2 cosinusoidy: A₀ = 0 V, A₁ = 10 V, f₁ = 100 Hz, A₂ = 4 V, f₂ = var, M = 16, f_S = 800 Hz

f2	Hz	200	250	300	350	400	450	500	600	700	800	900	1000	1100
f2p	Hz	200	250	300	350	brak	350	300	200	100	0	100	200	300
np	_	2	2,5	3	3,5	brak	3,5	3	2	1	0	1	2	3

f2	Hz	1300	1400	1500	1600	1700	1900	2200	2600	2900	3200	3500	3900	4100
f2p	Hz	300	200	100	0	100	300	200	200	300	0	300	100	100
np	_	3	2	1	0	1	3	2	2	3	0	3	1	1

Sprawdzamy, czy ostatnie dwie nastawione wartości f­₂ są zgodne ze wzorem

Skutek zmiany kąta fazowego drugiej cosinusoidy o 180°.

Obliczenia częstotliwości f_2p dla dwóch wartości częstotliwości f₂: 1500 i 2200 Hz

100Hz

200Hz

Wnioski:

1. faza odbitej składowej widma ulega zmianie na przeciwną,

2. wyniki wszystkich obliczeń są zgodne z wynikami pomiarów.

3.3. Przeciwdziałanie nakładaniu się składowych widma

Zastosowanie nadpróbkowania

Mierzymy pierwszych 7 harmonicznych fali prostokątnej. Obliczamy minimalną liczbę próbek

2(n_max + 1)= 2(7 + 1) = 16 i częstotli­wość próbkowania
Mf₁ = 16⋅100 = 1600 Hz

Przy nadpróbkowaniu zwiększamy liczbę próbek i częstotli­wość próbkowania 16-krotnie.

Wyniki pomiarów Tabela 8

Sygnał - fala prostokątna: A₁ = 10 V, f₁= 100 Hz, A₀ = 7.5 V, w = 0.125, M = 16, f_S = 1600 Hz;

M_N = 256, f_SN = 25600 Hz; M_F = 32, f_SF = 1600 Hz; M_FN = 64, f_SFN = 3200 Hz

Lp.	Częstotliwość	Amplitudy harmonicznych
		harmonicznej	teoretyczne	bez filtru dla fS	bez filtru dla fSN	z filtrem dla fSF	z filtrem dla fSFN
_	Hz	V	V	V	V	V
1.	100	4.8725	4.9039	4,8726	4,8726	4.8725
2.	200	4.5016	4,6194	4,5020	4,5019	4,5017
3.	300	3.9211	4,1573	3,9220	3,9221	3,9212
4.	400	3.1831	3,5355	3,1844	3,1882	3,1833
5.	500	2.3526	2,7779	2,3541	2,3744	2,3529
6.	600	1.5005	1,9134	1,5019	1,5670	1,5009
7.	700	0.6961	0,9755	0,6969	0,8153	0,6965

Zastosowanie filtru dolnoprzepustowego

Włączamy filtr antyaliazingowy o częstotliwości granicznej f_gr = 800 Hz, czyli nieco większej od częstotliwości siódmej harmonicznej i wykonujemy pomiary harmonicznych przy częstotliwości próbkowania f­_SF = 1600 Hz i liczbie próbek M_F = 2M = 32.

Z analizy kształtu charakterystyki filtru U_wy(f) wynika, że stosunek napięcia wyjściowego do wejściowego wynosi: dla f = 700 Hz − 100 %

Zastosowanie filtru dolnoprzepustowego i nadpróbkowania

W celu zmniejszenia skutków zjawiska aliazingu stosujemy niewielkie nadpróbkowanie: zwiększamy 2-krotnie częstoliwość próbkowania do wartości f­_SFN = 1600 Hz i liczbę próbek do wartości M_FN = 64. Wyniki wszystkich pomiarów wpisujemy do tabeli 8.

Obliczamy względne błędy pomiaru amplitudy 2 harmonicznej, odniesione do wartości teoretycznej A_t.

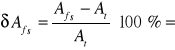
2,6%

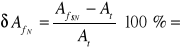
0,009%

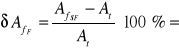
0,007%

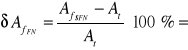
0,002%

Wniosek

Ze względu na skuteczność eliminacji zjawiska nakładania się składowych widma szeregujemy użyte metody w następującej kolejności:

1. filtrowanie z nadpróbkowaniem

2. nadpróbkowanie,

3. filtrowanie

4. Uwagi o wynikach pomiaru

Ćwiczenie wykonywane było w programie AH_CPSE, nie znamy jego dokładności obliczeniowej (długość mantysty, błędy obcięcia itp.), wpływającej na dokładność wyników pomiarów, które otrzymywaliśmy w trakcie wykonywania ćwiczenia.

2

---