POLITECHNIKA ŚWIĘTOKRZYSKA
LABORATORIUM FIZYKI
Numer ćwiczenia: M7	Temat ćwiczenia: Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła fizycznego Katera	Zespół: Mazur Karol Chudka Grzegorz
Data wykonania: 13.03.2007	Data oddania do sprawdzenia: 21.03.2007	Ocena:

Wstęp teoretyczny:

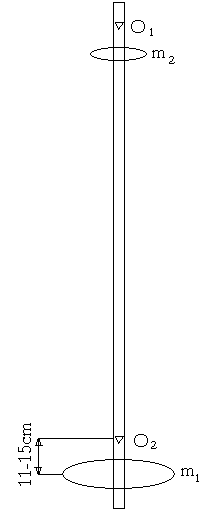
Okres drgań T wahadła matematycznego (punkt materialny o masie m, zawieszony na nieważkiej i nierozciągliwej nici o długości l), dany jest wzorem:

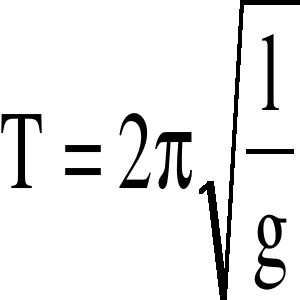
Znając okres drgań T i długość l wahadła, można obliczyć wartość przyspieszenia, które uzyskują ciała spadające swobodnie w danym miejscu na powierzchni Ziemi, czyli wartość przyspieszenia ziemskiego g. Wahadło matematyczne jest abstrakcją i w praktyce bywa zastępowane przez kulkę o realnym rozmiarze, zawieszoną na zwykłej nici lub na drucie. Powoduje to dodatkowe błędy przy wyznaczaniu przyspieszenia ziemskiego g. Dlatego też, aby tę wielkość wyznaczyć dokładniej, wykorzystuje się grawitacyjne wahadła fizyczne, to jest ciała sztywne, wykonujące ruch periodyczny wokół osi poziomej.

Wahadło rewersyjne przedstawione obok składa się z pręta, na którym można przesuwać dwie masy w postaci krążków m₁ i m₂. W tym eksperymencie krążek m₁ pozostaje w tym samym położeniu, a krążek m₂ może być przesuwany pomiędzy ostrzami O₁ i O₂. oddalonymi od siebie o
 . Odległość obu ostrzy może być wyznaczona z dużą dokładnością np. za pomocą specjalnej suwmiarki. Pręt może być zawieszony na jednym albo na drugim ostrzu. Dowiedziono, że można znaleźć takie położenie krążka m₂ na pręcie, przy którym okresy drgań wahadła zawieszonego na ostrzach O₁ i O₂ są takie same, czyli T₁ = T₂. Wtedy odległość L obu ostrzy, zwana długością zredukowaną, jest równa długości idealnego wahadła matematycznego o takim samym okresie. Wystarczy podstawić L i T₁ = T₂ do wzoru i wyznaczyć g. Dokładność wyznaczenia wartości g tą metodą jest wysoka, ze względu na precyzyjne określenie długości L wahadła zredukowanego i dokładniejsze wyznaczenie jego okresu na podstawie punktu przecięcia dwu krzywych.

Pomiary i obliczenia:

L.p.	Ilość wahnięć	Odległość między masami [cm]	Czas t1 [s]	Okres T1 [s]	Czas t2 [s]	Okres T2 [s]
1.	20	111	41,92	2,10	42,12	2,11
2.	20	101	40,31	2,01	40,97	2,05
3.	20	91	39,91	1,99	40,19	2,01
4.	20	81	39,72	1,98	39,19	1,96
5.	20	71	39,66	1,97	38,75	1,94
6.	20	61	39,59	1,97	38,44	1,92
7.	20	51	39,69	1,98	39,06	1,95
8.	20	41	40,22	2,01	40,72	2,04
9.	20	31	40,15	2,00	43,66	2,18

Odległość	Czas t [s]	Ilość wahnięć	Okres T [s]
33 cm	115,86	50	2,3172
98 cm	112,74	50	2,22548

Obliczam średnią wartość okresu wahań ze wzoru:

gdzie

-okres wahań dla położenia mas odpowiadającego punktom
;

-okres wahań dla położenia mas odpowiadającego punktom
;

Obliczam wartość przyśpieszenia ziemskiego ze wzoru:

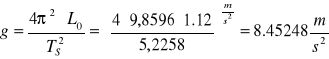
gdzie

-odległość między ostrzami O₁ i O₂

Rachunek błędów:

Metoda pomiaru przyśpieszenia ziemskiego za pomocą wahadła fizycznego Katera należy do dokładniejszych ze względu na to, iż występujące we wzorze końcowym wielkości L oraz T są wyznaczane z dużą precyzją.

Wyznaczenie błędu pomiaru:

• ∆l=0,001m

• ∆T=0,01s

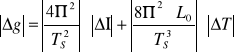
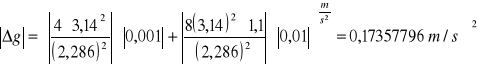
|∆g|=0,173577996m/s²

Przyśpieszenie ziemskie wynosi g=9,9~0,10m/s²

Wnioski:

Przeprowadzając w ten sposób doświadczenie możemy z dużą dokładnością wyznaczyć

przyśpieszenie ziemskie. Ważne jest aby starać się dokładnie odczytywać okresy drgań oraz

nie działać na wahadło zbyt dużą siłą, czyli nie powodować zbyt dużych wychyleń. Ponieważ wpływa to bezpośrednio na odczyt przyśpieszenia ziemskiego.

Otrzymujemy na wykresie krzywe zbliżone do paraboli o bardzo dużym kącie rozchylenia i w następstwie dwa punkty przecięcia. Powstały błąd w wyznaczaniu przyśpieszenia ziemskiego wynika z:

• nieprawidłowego odczytania pomiaru czasu poszczególnych wahnięć

• niejednakowych kątów wahnięć

Wyliczona wartość przyśpieszenia nie mieści się w granicach błędów.

1

---