PIERŚCIENIE NEWTONA

Cel ćwiczenia:

Celem wykonywanego doświadczenia jest poznanie zjawiska interferencji występującego w klinie optycznym oraz wykorzystanie tego zjawiska do celów pomiarowych.

Zestaw przyrządów:

- mikroskop interferencyjny,

- poczerniana płytka płasko-wypukła,

- lampa spektralna z oświetlaczem,

- komplet badanych soczewek,

Przebieg pomiarów:

1. Oświetlając przez płytkę dzielącą układ soczewka + płytka, znaleźć obraz prążków interferencyjnych.

2. Za pomocą podziałki mikrometrycznej określić średnicę mierzonego prążka, mierząc na podziałce mikroskopu wartość z lewej i prawej strony prążka.

Promień tego prążka wynosi:

r_u=(a_k^l-a_k^p)/2

3. Pomiar wykonać kilkakrotnie.

4. Obliczyć długość fali światła dla lampy spektralnej ze wzoru:

gdzie: R- promień krzywizny soczewki

r_u- wyznaczany promień K- tego prążka

Dla lampy sodowej λ=586[mm]

5. Wyznaczyć promień krzywizny soczewki

gdzie: λ- długość fali dla światłą sodowego

6. Ocenić dokładność dokonanych odczytów:

7. Obliczyć błąd względny i bezwzględny wyznaczonego promienia R.

Teoria:

PIERŚCIENIE NEWTONA

Interferencyjne prążki równej grubości, powstające w świetle przechodzącym lub odbitym w pobliżu miejsca zetknięcia się powierzchni wypukłej (np. sferycznej) z płaszczyzną.

Interferencja zachodzi w cienkiej warstwie powietrza rozdzielającej stykające się ciała. Przy monochromatycznym oświetleniu obserwuje się układ jasnych i ciemnych pierścieni odpowiadających liniom stałej grubości optycznej, a zatem i geometrycznej, ponieważ współcz. załamania powietrza jest bliskie 1. W świetle przechodzącym maksima luminencji występują dla t=(m-d)λ/2 gdzie:

m - liczba całkowita,

t - grubość warstwy powietrza,

λ - długości fali,

α - suma przesunięć fazowych przy odbiciu światła od obu powierzchni dzielona przez 2 Π.

Dla tych samych wartości t w świetle odbitym obserwuje się minima luminencji.

Ponieważ odległość między prążkami odpowiada zmianie grubości warstwy powietrza o λ/2, pierścienie Newtona służą do pomiaru promieni krzywizny soczewek i kontroli regularności kształtu powierzchni wypukłych i płaskich. Promień krzywizny pow. sferycznej można obliczyć według wzoru:

ϕ=(r²n-r²m)/λ(n-m)

gdzie: ru i rm - promienie n-ego i m-ego ciemnego prążka w świetle odbitym.

Luminencja prążków zależy nie tylko od natężenia światła przechodzącego, lecz także od współcz. R, oraz t, λ, α. Ze względu na stosunkowo małe wartości R obserwowane pierścienie są na ogół bardzo rozmyte. Pokrycie stykających się powierzchni półprzezroczystą warstewką srebra pozwala na uzyskanie prążków bardzo ostro zarysowanych, a tym samym na dokładną ocenę gładkości powierzchni. Przy oświetleniu światłem białym obserwuje się przy małych grubościach zbiór różnobarwnych pierścieni (położenie prążków dla różnych R jest różne). Dla większych grubości prążków grubości się nie obserwuje.

Zasada powstania pierścieni Newtona:

Doświadczenie opiera się na zjawisku załamania i częściowo odbicia światła przy przejściu wiązki światła przez granicę dwóch ośrodków o różnych współczynnikach załamania. Jeżeli dwie powierzchnie graniczne tworzą klin, to wiązki odbite od nich wzajemnie ze sobą interferują. Za przykład może posłużyć powietrzny klin interferencyjny utworzony pomiędzy dwiema wewnętrznymi powierzchniami P₁ i P₂ płasko równoległych

płytek szklanych. Fale odbite nakładają się we wszystkich punktach powierzchni P₁. Amplitudę zinterferowanej fali określa różnica dróg optycznych promieni padających - D. Przy założeniu, że kąt klina jest bardzo mały, równoległa wiązka światła monochromatycznego pada na powierzchnię klina prostopadle, możemy obliczyć różnicę dróg optycznych interfeniującymi promieniami. Określa to zależność : gdzie h jest grubością klina w danym miejscu. W miejscach gdzie D wynosi : k = 0,1,2,… n nastąpi wygaszenie światła na skutek interferencji, a dla Δ=(k+1)λ k = 0,1,2,…n nastąpi wzmocnienie światła. W klinie o płaskich powierzchniach zaobserwujemy więc na jasne i ciemne prążki. Tak zwany prążek zerowy (k=0) powstaje w miejscu styku obu powierzchni czyli na krawędzi klina. Pierwszy (k=1) na wysokości itd.

Prążki interferencyjne najłatwiej jest zaobserwować umieszczając na płaskiej płytce szklanej wypukło-sferyczną soczewkę. Powstaje wówczas między powierzchni płytki, a powierzchnią soczewki klin powietrzny o zmieniającym się kącie. Prążki powstające w takim klinie mają kształt kolisty. Nazywamy je prążkami Newtona. W miejscu styku soczewki i płytki powstaje ciemny (zerowy) prążek, natomiast kolejne prążki coraz bardziej się zagęszczają, aż przestaną być zauważalne.

Prążki Newtona można wykorzystać do wyznaczania promienia krzywizny soczewki

( R ) trzeba w tym celu znad długości fali i użytego światła oraz zmierzyć promień ( r ) dowolnego k-tego ciemnego prążka Promień krzywizny soczewki oblicza się ze wzoru na promień czaszy sferycznej o promieniu podstawy ( r ) i wysokości ( h ):

Znając długość fali oraz promień k-tego prążka kołowego ( r ) można wyznaczyć promień krzywizny soczewki. Do obserwacji używa się przyrządu jak na rysunku:

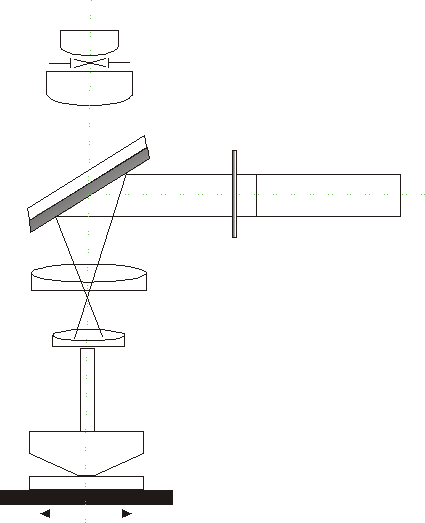
Jest to mikroskop na którego stoliku umieszczona jest płytka P i mierzona soczewka LO. Poprzez obiektyw oświetlone równoległą wiązką światła monochromatycznego z oświetlacza, odbitego od zwierciadła półprzepuszczalnego Z umieszczonego nad obiektywem mikroskopu. W okularze „umieszczony” jest krzyż celowniczy, którym ustawia się na wybrany obraz prążka. Należy dokonać pomiaru promienia wybranego prążka, poprzez odczytanie wskaźników przesunięcia lewostronnego i prawostronnego (a_k^l) ; (a_k^p)

Opisuje to zależność:

Dzięki znajomości długości fali świetlnej, można obliczyć promień krzywizny soczewki. Mając już obliczony promień możemy odwrócić przebieg doświadczenia i po przekształceniu wzoru na promień obliczyć nieznaną długość fali świetlnej, wydzielonej z wiązki światła białego poprzez założenie na oświetlacz filtra interferencyjnego.

Wzory:

1) - długość fali światła dla lampy spektralnej (l. sodowa)

W naszym przypadku: λ=586mm

2) - promień krzywizny soczewki

3) - promień danego prążka

gdzie:

k - numer mierzonego prążka, mierzonego w kolejności od środka

a_k^L - wartość z lewej strony prążka odczytana na podziałce mikrometru

a_k^P - wartość z lewej strony prążka odczytana na podziałce mikrometru.

Wzory do obliczeń Błędów „R”

Promień krzywizny soczewek

- błądbezwzględny

- błąd względny

Wyniki wraz z obliczonymi błędami i dyskusją błędów:

Soczewka nr 1.

K	prawa strona [mm]	lewa strona [mm]	rk [mm]	λ [mm]	R [m]
1	83	84	0,5	586	0,43
2	82,8	84,1	0,65	586	0,36
3	82,5	84,3	0,9	586	0,46

1.

2.

3.

1.

2.

3.

Soczewka nr 2.

K	prawa strona [mm]	lewa strona [mm]	rk [mm]	λ [mm]	R [m]
1	83,1	84	0,45	586	0,34
2	82,8	84,1	0,65	586	0,36
3	82,6	84,3	0,85	586	0,41

1.

2.

3.

1.

2.

3.

Soczewka nr 3.

K	prawa strona [mm]	lewa strona [mm]	rk [mm]	λ [mm]	R [m]
1	81,3	81,8	0,25	586	0,11
2	81,2	82,2	0,5	586	0,21
3	81,8	82,8	0,5	586	0,14

1.

2.

3.

1.

2.

3.

Wnioski:

Tematem ćwiczenia był pomiar pier ścieni Newtona powstających na skutek przejścia lub odbicia światła w pobliżu miejsca zetknięcia się powierzchni wypukłej (w naszym przypadku soczewki) z płaszczyzną.

Dzięki wykorzystaniu światłą lampy sodowej (światła monochromatycznego o jednakowej długości fali świetlnej zaobserwowałem układ ciemnych i jasnych pierścieni (na przemian).

Ponieważ promienie poszczególnych pierścieni zależą od grubości warstwy powietrza między soczewką a płaszczyzną, mierząc wartości tych promieni i wykorzystując wzór XXXXXXXX można obliczyć promień krzywizny soczewki. Jeżeli natomiast znanmy promień krzywizny soczewki R (można go zmierzyć tzw. sferometrem) przekształcając powyższy wzór jesteśmy w stanie określić długość fali świetlnej XX padającej na badaną soczewkę.

Pierścienie Newtona Służą również do kontroli regularności kształtu powierzchni (wypukłych i płaskich).

W przeprowadzonym ćwiczeniu sprawdziłem również jak zachowuje się światło przechodząc przez płaską płytkę i przez klin. Płytka nie powodowała powstania żadnych zjawisk świetlnych, co może oznaczać, że światło przechodząc przez płytkę odbija się pod tym samym kątem co światło padające.

Klin natomiast powodował odbicie się światła w taki sposób iż w mikroskopie zaobserwowano równoległe do siebie przechodzące linie świetlne, tak jak w przypadku soczewki na przemian ciemne i jasne.

Odczyt wartości ciemnego i jasnego promienia obarczony jest dużym błędem z powodu nie punktowego przylegania soczewki do płytki.

Błąd wynika z niedokładności przyrządów pomiarowych. Przyjąłem 0,05 mm, co dla wartości promieni rzędu kilku dziesiętnych milimetra co stanowi dość dużą odchyłkę i możliwość popełnienia sporych błędów.

2

---