1. Jaka jest ilość istotnych efektów głównych w analizie wariancji 2x2x3?

A 3 B 5 C 10 D 30

2. Jaka jest maksymalna ilość istotnych interakcji w analizie wariancji 2x2x3?

A 3 B 4 C 5 D 10

3. Jaka jest maksymalna ilość prostych efektów głównych badaniu 2x4?

A 2 B 3 C 5 D 6

4. Ile grup występuje w badaniu 2x2x3(bez powtarzanych pomiarów)?

A 3 B 7 C 18 D 22

5. Wzór wyników wskazuje na wystąpienie:

	Niska frustracja	Wysoka frustracja
Niski lęk	3,5	6
Wysoki lęk	6	3,5

A istotnego efektu głównego frustracji

B istotnego efektu głównego lęku

C istotnego efektu interakcji

D istotnego efektu głównego frustracji oraz istotnego efektu interakcji

6. Wzór wyników wskazuje na wystąpienie:

	Niska frustracja	Wysoka frustracja
Niski lęk	3,5	7
Wysoki lęk	6	4,5

A istotnego efektu głównego frustracji

B istotnego efektu głównego lęku

C istotnego efektu interakcji

D istotnego efektu głównego frustracji oraz istotnego efektu interakcji

7. Wzór wyników wskazuje na wystąpienie:

	Niska frustracja	Wysoka frustracja
Niski lęk	3,5	5
Wysoki lęk	7	8,5

A istotny efekt główny frustracji i istotny efekt główny lęku

B istotny efekt główny lęku i istotny efekt interakcji

C istotny efekt główny frustracji i istotny efekt interakcji

D istotny efekt główny frustracji, lęku i interakcji

8. Jaka jest ilość df w analizie wariancji 2x2?

A 1 B 2 C 3 D 5

9. Dodatkowa analiza zmierzająca do oszacowania istotności i kierunku prostych efektów głównych zalecana jest w przypadku stwierdzenia w analizie wariancji:

A jednego lub więcej istotnych efektów głównych

B istotnych interakcji dwóch zmiennych

10. Dodatkowa analiza zmierzająca do oszacowania istotności i wzoru interakcji prostych zalecana jest przypadku stwierdzenia w analizie wariacji:

A więcej niż jednego istotnego efektu głównego

B więcej niż jednej istotnej interakcji dwóch zmiennych

C istotnej interakcji trzech zmiennych

11. Wydruk analizy wariancji dla danych z powtarzanymi pomiarami zawiera 8 oszacowań wartości F dla każdego efektu. Oszacowania te są zawsze identyczne gdy:

A jest tylko jedna zmienna niezależna

B żadna ze zmiennych niezależnych nie występuje na więcej niż dwóch poziomach

12. W analizie wariancji dla danych z powtarzanymi pomiarami założenie o sferyczności nie musi być spełnione gdy:

A żadna ze zmiennych niezależnych nie występuje na więcej niż dwóch poziomach

B stosowane jest rozwiązanie wielozmiennowe

C stosowany jest test Huynh-Feldta, Greenhouse-Geissera lub Lower-band

D wszystkie odpowiedzi są prawidłowe

13. Tabela zawiera wyniki eksperymentu 2x2x2 nad wpływem zmiennych niezależnych AxBxC na zmienną zależną. Liczby dotyczą średniego poziomu zmiennej zależnej w ośmiu grupach. Jeśli założyć istotność wszystkich występujących różnic to przedstawiony wzór wyników wskazuje na wystąpienie:

A1 A2

		B1		B2
C1		10		24
C2		24		10
		B1		B2
C1		24		10
C2		10		24

A istotnych efektów głównych zmiennych A, B, C

B istotnych interakcji AxBxC

C istotnych efektów głównych zmiennych A, B, C oraz istotnej interakcji AxBxC

D żadna odpowiedź nie jest poprawna

14. W którym schemacie badania wystąpić mogą istotne interakcje (sprawdzić to pytanie)

A 2x2

B 2x3

C 2x2x3

D wszystkie

15. W analizie kowariancji:

A współzmienna musi być skorelowana ze zmienną zależną

16. Analiza kowariancji stosowana jest zamiast analizy wariancji gdy chcemy:

A zmniejszyć błąd losowy

B statystycznie wyrównać wyjściowe różnice między grupami

C zmniejszyć błąd losowy lub/i statystycznie wyrównać wyjściowe różnice między grupami

17. Metoda głównych składowych to jedna z metod należących do rodziny:

A w analizie czynnikowej

18. W równaniu regresji jeśli korelacja między zmienną przewidywaną Y a predykatorem X wynosi 0 i jeśli nie ma innych predyktorów to wartość zmiennej przewidywanej Y równa się:

A średniej Y

B średniej X

C 0

19. Gdy zmienna X, której chcemy użyć jako predyktora w równaniu regresji mierzona jest na skali nominalnej i ma więcej niż 2 poziomy konieczne jest jej przekształcenie na kilka nowych predyktorów, z których każdy ma tylko 2 poziomy (dummy coding). Ile takich nowych prektorów musimy utworzyć w przypadku, gdy zmienna ma 5 poziomów:

A 4 (zawsze o jeden mniej)

20. Badacz interesuje się zależnością między płcią studenta, płcią wykładowcy a preferencją do siedzenia na wykładzie w przedniej lub tylnej części klasy. W analizie wyników zastosowana test chi kwadrat (2x2x2). Wadą takiej analizy jest:

A niemożność stwierdzenia czy występuje statystycznie istotna interakcja

21. Zastosowanie testu chi kwadrat prowadzi czasem do trudności w ustaleniu, które kombinacje poziomów dwóch zmiennych odpowiedzialne są za istotną zależność. Trudność taka dotyczy, którego ze schematów:

A 2x2

B 3x5

C 2x2x2

D wszystkie

22. W analizie czynnikowej, arbitralne decyzje badacza dotyczące rodzaju i parametrów przeprowadzonej analizy:

A mają wpływ na ilość czynników i stopień ich skorelowania

B mają wpływ na wielkość korelacji między czynnikami, ale nie na ilość czynników

C mają wpływ na ilość czynników, ale nie na ich skorelowanie

D nie mają wpływu na ilość czynników ani na stopień ich skorelowania

23. Przedstawione wyniki analizy wyjściowej uwzględniają(do badania z przedmiotami):

A 6 zmiennych wyjściowych i 2 czynniki

24. W przedstawionej analizie czynnikowej korelacja między czynnikami:

A wynosi 0

25. Wedle powszechnie przyjętej klasyfikacji, wartość eta = 0,5 oznacza:

A mały efekt

B średni efekt ???????/

C duży efekt

D brak efektu

26. Praca semestralna studenta stanowi replikację badania wcześniejszego, ale na mniejszej próbie. Można oczekiwać, że w porównaniu z wynikami oryginalnego badania, wyniki pracy semestralnej wykażą:

A podobną siłę efektu i podobny poziom istotności

B niższą siłę efektu

C podobną siłę efektu, ale mniej istotne wyniki

27. Weryfikacja hipotez postawionych w badaniu z wykorzystaniem efektu Stroopa dla

pokazania ...... kategoryzacji społecznej wymaga analizy:

B) wariancji z powtarzanym pomiarem w układzie 2X2 (rasa osoby bodźcowej X czcionka)

28. Najbardziej konserwatywny test istotności dla efektów wewnątrzobiektowych to:

C) Lower bound

29. Z testu sferyczności założonej można korzystać gdy:

Test sferyczności jest nieistotny

30. Lambda Wilksa i ślad Pilai to:

przykłady testów wielu zmiennych

31. Testy wielu zmiennych przy powtarzanym pomiarze można stosować:

1. Zawsze

32. W eksperymencie (2)X2 z użyciem counterbalansingu:

Poziom zmiennej niezależnej bez powtarzanych pomiarów decyduje o kolejności poziomów zmiennej niezależnej z powtarzanym pomiarem.

33. Efekt główny counterbalansingu w eksperymencie (2)X2 pokazuje:

3. że, to który pomiar był wykorzystany wcześniej powoduje różnice w wartościach

zmiennej zależnej

34. Nieprawdą jest że w analizie kowariancji:

1. zmienna zależna jest dostosowana ze względu na różnice indywidualne w zakresie

innej mierzonej zmiennej

2. analiza kowariancji pozwala odróżnić statystyczny wpływ zmiennych ubocznych od

wpływu zmiennej niezależnej.

3. Analizą kowariancji można posłużyć się w celu wyeliminowania wstępnych różnic

między grupami.

4. Wszystkie odpowiedzi są poprawne

35. W analizie kowariancji df dla współzmiennej

wynosi 1

36. Nieprawdą jest, że w analizie kowariancji:

1. współzmienna musi być skorelowana ze zmienną zależną

2. współzmienna może być wyjaśniana poziomami zmiennej zależnej (przed manipulacją eksperymentalną)

3. może być tylko 1 współzmienna

37. Przewagą podziału badanych na grupy wyznaczone dwoma poziomami współzmiennej nad analizą kowariancji z tą współzmienną jest:

1. możliwość wykonania analizy wariancji z dodatkową zmienną niezależną i sprawdzenia czy wchodzi ona w interakcję z pozostałymi zmiennymi niezależnymi

38. Jeżeli współczynnik korelacji wynosi r=0,6 to współczynnik determinacji (R2) wynosi:

1. 36

2. 36% - współczynnik wariancji

3. 0,36

4. 0,0036

39. w analizie regresji do przewidywania poziomu zmiennej Y (zależnej) używa się info:

1. o średnim poziomie zmiennej Y w populacji oraz o zmiennej X (zależnej) skorelowanej ze zmienną Y.

40. możliwość skutecznego przewidywania poziomu jednej zmiennej na podstawie innej zmiennej:

1. oznacza, że zależność jest przyczynowa

2. oznacza, że zależność jest przyczynowa i pokazuje która zmienna jest przyczyną a która skutkiem

3. oznacza że zależność nie jest przyczynowa, ale pokazuje co jest zmienną objaśniającą a co objaśnianą.

4. Żadna nie jest prawdziwa

41. gdy jakaś zmienna której chcemy użyć jako predyktora w analizie regresji mierzona jest na skali nominalnej ma więcej niż 2 poziomy...............

1. jej przekształcenie na kilka predyktorów z których każdy ma tylko 2 poziomy

2. wykonanie dummy coding

42. metodą której warto użyć dla przewidywania czasu odrabiania lekcji w oparciu o płacenie za stopnie, średnią ocen ucznia, ilość godzina spędzanych na nauce itp...

b) regresja wielokrotna

43. Poniższy wykres może ilustrować wyniki eksperymentu:

- jednozmiennowego z czterema grupami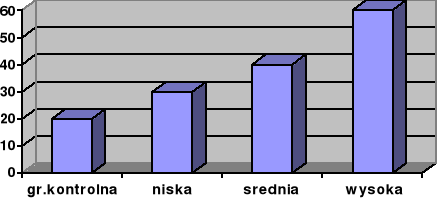


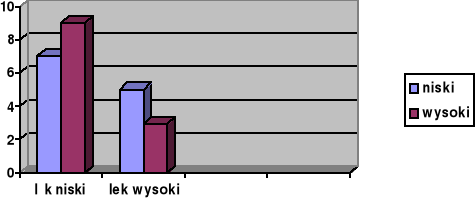
44. Poniższy wykres może ilustrować wyniki eksperymentu:

• wielozmiennowego 2x2




45. Poniższy wydruk analizy wariancji pokazuje istotny;

efekt interakcji frustracji i lęku oraz efekt główny lęku (test efektów międzyobiektowych)

46. Ponizsza tabela wskazuje:

efekt główny zmiennej IV 1 =20

IV1 poz 1 IV2 poz 2

IV2 poz 1 20 40 +20

IV2 poz 1 20 40 +20

=0 =0

47. Analiza wariancji dla trzech zmiennych niezależnych daje:

1. 3 efekty główne

2. 3 interakcje (AB AC BC)

3. interakcje 3 zmiennych

4. wszystkie odpowiedzi prawdziwe

48. Istotna interakcja 3 zmiennych występuje, gdy:

• interakcja dwóch zmiennych niezależnych zmienia się w zależności od poziomu trzeciej zmiennej niezależnej

49. Poniższy wykres ilustrujący wyniki z tabeli pokazuje:

1. przy wyższym lęku mniejsza agresja

2. efekt główny zmiennej lęk

3. interakcja zmiannej lęk i frustracja

4. wszystkie odpowiedzi są prawdziwe




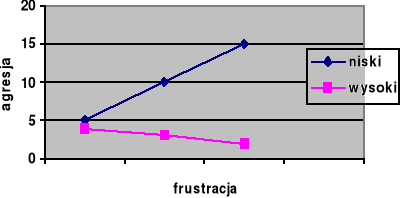
50. W eksperymencie 2x2 efekt interakcji wyst. Gdy:

b) proste efekty główne zmiennej niezależnej sąróżne

c) wpływ jedenj zmiennej niezaleznej na zmiennązalezną jest różny w zalezności od poziomu drugiej zmiennej niezależnej

d) odpowiedzi c i b są prawdziwe.

51. W eksperymencie 2x3 jest:

• 6 prostych efektów głównych

52. W eksperymencie 2x3 jest:

• jedna interakcja

53. Proste efekty główne pokrywają się z prostymi porównaniami parami, gdy:

• wszystkie zmienne niezależne występują na dwóch poziomach

54. Która informacja o interakcjach nie jest prawdziwa:

• Są istotne dopiero przy istotnych efektach głównych danych zmiennych

55. Testy post hoc w porównaniu z porównaniami parami:

1. Są bardziej konserwatywne

2. testy post hoc stosowane są szczególnie często gdy zmienne występują na więcej niż3 poziomach

d) a i b są prawdziwe

56. Test Tukeya, Scheffyego i Bonnferoniego to:

• porównania post hoc

57. Interakcja prosta dwóch zmiennych w układzie 2x2x2 to:

1. interakcja zachodząca przy danym poziomie trzeciej zmiennej

2. jedyna interakcja potrójna

3. interakcja przy uśrednieniu dwóch interakcji

58. Ilość df dla interakcji jest równa:

• iloczynowi df dla każdego efektu głównego

59. Counetrbalansing to:

• losowy dobór do grup różniących się kolejnością poziomów zmiennych niezależnych

60. Badanie z wykorzystaniem efektu Stroopa do bad. kategoryzacji społecznej pokazało:

1. badanie z powtarzanym pomiarem dla rożnych kolorów czcionki

2. dla różnych osób bodźcowych

3. rasy osoby bodźcowej

4. wszystkie odpowiedzi są prawdziwe

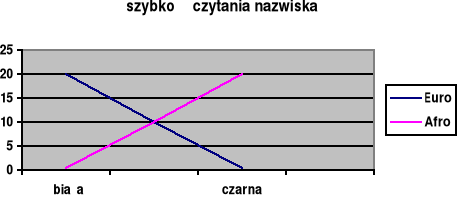
61. Przy założeniu, że wszystkie widoczne na rys. efekty są istotne można powiedzieć, że:

• badani czytają szybciej nazwiska Euroamerykanie gdy są napisane białą czcionką (niż czarną) zaś Afroamerykanie czytają szybciej, gdy są napisane czarną czcionką.

62. Co najmniej jedna współzmienna występuje zawsze w:

analizie kowariancji

63. Przedstawione wyniki tabeli uwzględniają:

1 2

fran ,960

niem

lacina

mate

rys

muzyka

• odpowiedź: 6 zmiennych wyjściowych i dwa czynniki

64. Szare pole wskazuje istotny efekt:

- prosty zmiennej frustracja na poziomie niskiego lęku.

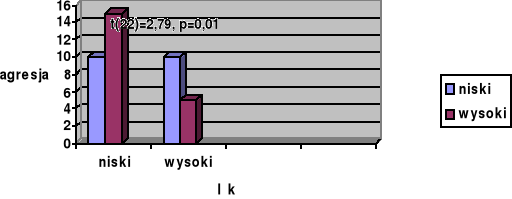
65. Ile efektów interakcji można znaleźć w : 2x3x2

Odp. 4

66. Analiza wariancji w układzie 2x2x2 (zapis)

• efekt główny frustracji: F(1,88)= 12.24; p=0,001

• efekt główny lęku: F(1,88)=17.77; p<0,001

67. Wykres ilustrujący wyniki badań z wykorzystaniem efektu Stroopa pokazuje, że:

wszystkie odpowiedzi są fałszywe

9

---