POLITECHNIKA ŚLĄSKA WYDZIAŁ ELEKTRYCZNY KATEDRA MECHATRONIKI
Laboratorium Mechaniki i Mechatroniki
Nr: 6	Temat: Drgania układów n-masowych - pomiary i symulacje
Wykonano: 23.11.2011			Oddano: 21.12.2011
	Prowadzący: dr inż. Paweł Kielan
	Nazwisko i Imię			Ocena		Data, podpis
Studia: SI Elektrotechnika Semestr: III Grupa: II Sekcja: II Dz. i godz. zajęć Środa, godz. 10^15	…………………………………………… …………………………………………… …………………………………………… …………………………………………… ……………………………………………			……… ……… ……… ……… ………

I. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z następującymi zagadnieniami:

- Zapoznanie się z możliwością wykorzystania środowiska Matlab-Simulink do symulacji

drgań układów elektromechanicznych;

- Opanowanie formalizmu Lagrange'a II rodzaju do formułowania dynamicznych równań

ruchu;

- Określenie częstotliwości rezonansowych dla n- masowego układu drgań skrętnych.

II. Wprowadzenie teoretyczne

Metoda Sztywnych Elementów Skończonych polega na skupieniu masy (tzw. dyskredytacji) , dzięki której z rzeczywistego układu o nieskończonej liczbie swobody otrzymujemy układ gdzie liczba swobody jest skończona. Następnie węzły, dla których dokonano skupienia masy (tzw. węzły redukcji) łączy się między sobą elementami sprężystymi i tłumiącymi. Dzięki tym zabiegom możemy obliczyć ruch korzystając z tzw. równań Lagrange'a oraz zależności na energię.

Równania Lagrange'a II rodzaju:

Metodę SES wykorzystuje się do obliczeń częstotliwości rezonansowych rzeczywistych układów przeniesienia napędów, stosuje się ją także do symulowania odkształceń, naprężeń, przemieszczeń a także do określenia wytrzymałość konstrukcji. Za pomocą tejże metody możliwe jest uzyskanie wyników dla skomplikowanych kształtów , dla których przeprowadzenie obliczeń analitycznych nie byłoby możliwe.

Zależności na energię dla ruchu liniowego i obrotowego:

III. Równania Lagrange'a dla układów

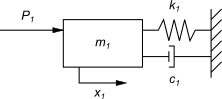
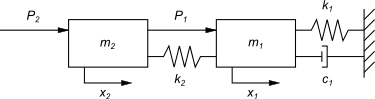
IV. Symulacje w programie Matlab - Simulink

Implementacja

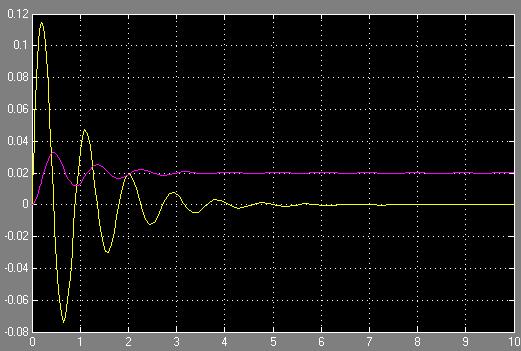
Przykładowy wykres dla parametru k = 2

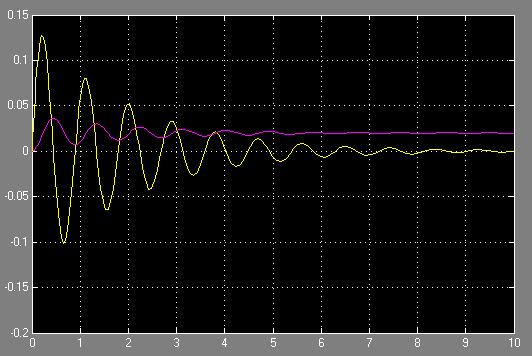
Przykładowy wykres dla parametru k = 1

Wyniki symulacji

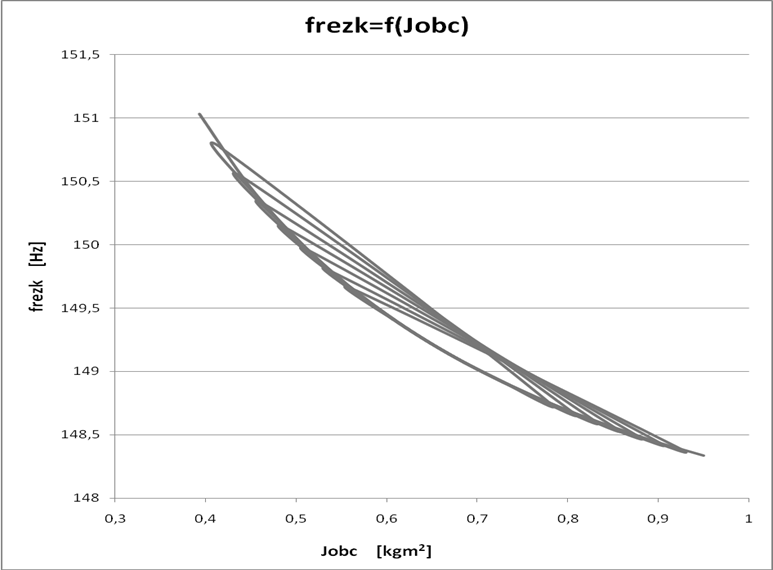
V. Wnioski

Dokonując symulacji przy pomocy programu Matlab-Simulink, uzyskaliśmy zależność momentu obciążenia i częstotliwości w zależności od wypełnienia tarczy bezwładnościowej krążkami, dla różnych konfiguracji wypełnienia tarczy.

Dla uzyskanych w wyniku symulacji pomiarów otrzymaliśmy charakterystykę malejącą frezk=f(Jobc), gdzie wraz ze wzrostem obciążenia tarczy obserwujemy spadek częstotliwości rezonansowej.

Także zmieniając parametry symulacji wykonywanej w punkcie IV zauważyliśmy znaczne różnice w charakterystykach wyjściowych badanego układu. Dla przykładu zwiększanie wartości parametru m oraz zmniejszanie k (współczynnika sprężystości) znacznie wydłużało czas potrzebny na ustabilizowanie się układu.