1. STAN GAZOWY

1.1. GAZY I PARY

Powietrze jest mieszaniną par i gazów. W warunkach wchodzących w zakres rozpatrywanej tematyki gazami są np.: azot, tlen, argon, natomiast pary to np.: para wodna, ditlenek węgla. Większość zanieczyszczeń powietrza to także pary, jak np. ditlenek siarki, pary rozpuszczalników organicznych. Przy rozpatrywaniu zagadnień związanych z właściwościami powietrza oraz gazów odlotowych, gdzie pary występują w mieszaninie z gazami i są zwykle znacznie rozcieńczone, nie ma potrzeby rozróżniać, który ze składników jest gazem a który parą. Upraszczając zagadnienie, wszystkie składniki możemy traktować jako gazy.

Wiele substancji (pierwiastków, związków chemicznych) może występować w trzech stanach skupienia (trzech fazach). Przez odpowiednią zmianę parametrów możemy powodować ich przemiany fazowe. Obszary występowania poszczególnych stanów skupienia przedstawiono na przykładzie wody, stanowiącej (jako para wodna) istotny składnik atmosfery. Ilustruje to rysunek 1.1.

Rys. 1.1. Wykres równowag fazowych dla wody (T_K - temperatura krytyczna)

Charakteryzując pokrótce trzy przedstawione na rysunku fazy można powiedzieć że:

• ciała stałe cechują się określonym kształtem i granicą faz, a cząstki je tworzące (atomy, jony lub cząsteczki) są umiejscowione w siatce krystalicznej i wykonują ruchy drgające,

• ciecze nie mają określonego kształtu, lecz przyjmują kształt naczynia, mają natomiast granicę faz, a cząstki, które je tworzą mogą zmieniać położenie względem siebie bez większych zmian odległości, o których decydują siły oddziaływania międzycząsteczkowego,

• gazy oraz pary nie mają własnego kształtu ani granicy faz, przyjmują objętość naczynia, które wypełniają, a odległości między cząstkami są znaczne, stąd siły wzajemnego oddziaływania są znikome (na ogół wręcz pomijalne).

Jak widać z przedstawionego wcześniej rysunku z gazem mamy do czynienia wtedy, gdy temperatura jest wyższa od temperatury krytycznej, T_K. Przykładowe wartości temperatury krytycznej wybranych składników i zanieczyszczeń powietrza przedstawiono w tabeli 1.1.

Tabela 1.1

Temperatury krytyczne wybranych składników powietrza

Substancja	Wzór chemiczny	Temperatura krytyczna, TK [K]
Azot	N2	126
Tlen	O2	154,3
Argon	Ar	150,7
Ditlenek siarki	SO2	430,6
Ditlenek węgla	CO2	304,2
Hel	He	5,1
Powietrze	-	132,4
Amoniak	NH3	405,5
Woda	H2O	647,1

Z danych zawartych w tabeli wynika, że w temperaturze pokojowej, 293 K, spośród wymienionych substancji, będących składnikami powietrza, ditlenek siarki, ditlenek węgla, amoniak, para woda są parami, a pozostałe gazami. Często parę określa się wręcz jako gaz znajdujący się w temperaturze mniejszej od temperatury krytycznej, T_K. W potocznym rozumieniu za parę, błędnie, uważa się obłoki mgły powstające w czasie kondensacji. Pary są równie przeźroczysta jak gazy.

Gazy i pary oraz ich mieszaniny, w warunkach tego samego przyciągania ziemskiego, są substancjami jednorodnymi i wywierają równomierne ciśnienie na ścianki naczynia, które zajmują. W skali całej atmosfery ziemskiej występuje jednak zróżnicowanie wartości ciśnienia oraz gęstości powietrza. Im większa odległość od powierzchni ziemi tym mniejsze wartości przyjmuje gęstość oraz ciśnienie.

1.2. PRAWA GAZU DOSKONAŁEGO

Stan określonej ilości gazu, wyrażonej liczbą kilomoli n (określanej mianem liczności), można opisać za pomocą trzech, ściśle ze sobą powiązanych parametrów:

• ciśnienia (wywieranego na ścianki naczynia) p, wyrażonego w paskalach, Pa,

• temperatury, wyrażonej w kelwinach, K,

• objętości, wyrażonej w metrach sześciennych, m³.

Niekiedy stan gazu opisujemy tylko dwoma parametrami, przez podanie ciśnienia i temperatury. Wtedy opis dotyczy dowolniej (nieokreślonej) ilości gazu.

Wzajemną zmienność powiązanych ze sobą parametrów gazów możemy opisywać prostymi równaniami, przy upraszczającym założeniu, że mamy do czynienia z gazem doskonałym. Pod tym pojęciem rozumiemy gaz stanowiący zbiór punktów materialnych nie oddziałujących na siebie siłami przyciągania i odpychania, poruszających się ruchem prostoliniowym, ulegających zderzeniom idealnie sprężystym.

Prawo Avogadro

Jednakowe objętości różnych gazów, w tych samych warunkach (ciśnienia i temperatury) zawierają taką samą liczbę cząstek. W uzupełnieniu można dodać kilka informacji dodatkowych.

• Jeden kilomol gazu zawiera 6,023 ∙ 10²⁶ cząstek.

• Jeden kilomol gazu przyjmuje objętość molową V_M. Jest to wielkość zmienna, zależna od parametrów. W warunkach normalnych (WN) przyjmuje ona wartość (V_M)_WN = 22,415 m³/kmol.

• Warunki normalne są umownie przyjętymi parametrami: ciśnienia, p_N = 101325 Pa oraz temperatury, T_N = 273,15 K

• W praktyce podane wyżej wielkości stosuje się w obliczeniach z mniejszą dokładnością: (V_M)_WN = 22,4 m³, p_N = 1,013 ∙ 10⁵ Pa, T_N = 273 K.

Z prawa Avogadra wynika praktyczna informacja - wykorzystywana w obliczeniach inżynierskich - że takie same ilości różnych gazów (wyrażone w kilomolach), w tych samych warunkach (temperatury i ciśnienia) przyjmują takie same objętości.

Prawo Boyla-Mariotte'a

W stałej temperaturze, dla określonej ilości gazu, iloczyn ciśnienia i objętości jest wielkością stałą. Matematyczny zapis prawa jest równaniem izotermy gazu.

p ∙ V = const (T = const) (1.1)

Prawa Gay-Lussaca

Dla określonej ilości gazu, pod stałym ciśnieniem stosunek objętości i temperatury jest wielkością stałą. Prawo opisuje równanie izobary.

(p =  const) (1.2)

Dla określonej ilości gazu, przy zachowaniu stałej objętości, stosunek ciśnienia i temperatury jest wielkością stałą. Prawo opisuje równanie izochory.

(V = const) (1.3)

Równanie stanu gazu doskonałego

Przedstawione wyżej zależności można (dla określonej, dowolnej ilości gazu) ująć w jedno równanie:

(1.4)

Stany 1 oraz 2 są dowolne (w zakresie parametrów, w którym dana substancja występuje w postaci gazu). Można zatem napisać:

(1.5)

Wartość liczbowa iloczynu (const) zależy od ilości rozpatrywanego gazu, wyrażonej w kilomolach, czyli jego liczności (n). Dla jednego kilomola gazu (n = 1) przyjmuje ona wartość szczególną, oznaczaną symbolem R, określaną jako uniwersalna stała gazowa. Jej wartość wynosi:

[J/(kmol∙K)] (1.6)

Przez
określona jest objętość molowa gazu w temperaturze T i pod ciśnieniem p. W dalszej części pracy może ona być - w sytuacjach gdy przyczyni się to do lepszej czytelności zapisu - oznaczana symbolem
, co informuje, że jej wartość zależy od wartości temperatury (T) oraz ciśnienia (p).

Z wymiaru stałej gazowej
wynika często formułowana jej definicja, iż jest to praca (wyrażona w dżulach [J]) jaką „wykona” 1 kilomol gazu podgrzany o 1 K, pod stałym ciśnieniem.

Równanie stanu gazu doskonałego, dla jednego kilomola gazu przyjmie postać:

p ∙ V_M = R∙ T (1.7)

Po uwzględnieniu, że całkowita objętość rozpatrywanej ilości gazu jest równa:

V = V_M ∙ n (1.8)

uzyskujemy równanie opisujące stan gazu, często używane w obliczeniach, nazywane równaniem Clapeyrona:

p ∙ V = n ∙ R ∙ T (1.9)

Prawo Daltona

Całkowite ciśnienie (p) wywierane przez mieszaninę gazów, nie reagujących ze sobą, jest równe sumie ciśnień jakie wywierałby każdy z gazów wchodzących w skład mieszaniny, gdyby sam został umieszczony w całej objętości zajmowanej przez mieszaninę, w tej samej temperaturze.

p = ∑p_i (1.10)

Ciśnienie pojedynczego składnika mieszaniny (p_i - ciśnienie parcjalne) zależy od jego ilości w mieszaninie, wyrażonej w kilomolach:

p_i ∙ V = n_i ∙ R ∙ T (1.11)

Ilość gazu całej mieszaniny wyrażona w kilomolach jest w tym wypadku równa:

n = ∑n_i ( 1.12)

Wzór Clapeyrona, dla mieszaniny gazów, można zatem wyrazić następująco:

p ∙ V = ∑p_i ∙ V = ∑n_i ∙ R ∙ T = n ∙ R ∙ T (1.13)

Przedstawione wyżej wzory służą do opisu określonej ilości gazu wyrażonej w kilomolach. Ilość gazu możemy również określać jako masę wyrażoną w kilogramach, m_i [kg]. Zamiana masy m_i na liczbę kilomoli n_i jest możliwa przy znajomości masy molowej rozpatrywanej substancji M_i [kg/kmol].

(1.14)

Stosując powyższą zależność możemy powiązać ciśnienie parcjalne rozpatrywanego składnika p_i z jego masą m_i zawartą w określonej objętości mieszaniny V:

(1.15)

W tabeli 1.2 podano masy molowe ważniejszych składników powietrza oraz typowych, gazowych zanieczyszczeń atmosfery.

Tabela 1.2

Masy molowe wybranych składników oraz zanieczyszczeń powietrza

Substancja	Wzór chemiczny	Masa molowa kg/kmol
Azot	N2	28,01
Tlen	O2	32,00
Argon	Ar	39,95
Ditlenek siarki	SO2	64,06
Ditlenek węgla	CO2	44,01
Ditlenek azotu	NO2	46,00
Tlenek azotu	NO	30,00
Woda	H2O	18,02
Tlenek węgla	CO	28,01
Amoniak	NH3	17,03
Acetaldehyd	CH3CHO	44,05
Aceton	CH3COCH3	58,08
Benzen	C6H6	78,11
Butanol	C4H9OH	74,12
Chlor	Cl	35,45
Chlorowodór	HCl	36,46
Formaldehyd	HCHO	30,03
Ksylen	C6H5 (CH3)2	107,17
Octan etylu	CH3COOC2H5	88,10
Octan butylu	CH3COOC4H9	116,16
Siarkowodór	H2S	34,02
Toluen	C6H5CH3	92,13

W większości prezentowanych dalej obliczeń będą stosowane wartości mas molowych z dokładnością do jednego miejsca po przecinku.

Przedstawione wcześniej zależności (równania od 1.1 do 1.15) opisują zachowanie gazu doskonałego. Do opisu gazów rzeczywistych stosuje się bardziej złożone wzory, w których uwzględnia się dane empiryczne. Najczęściej stosowany jest wzór van der Waalsa.

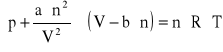
(1.16)

gdzie a oraz b są empirycznymi stałymi, charakterystycznymi dla danego gazu.

Powyższe równanie ma postać zbliżoną do równania Clapeyrona. Zawiera ono poprawkę na ciśnienie wynikające z sił oddziaływania między cząsteczkami gazu (a ∙ n²/V²) oraz poprawkę związaną z objętością własną cząstek gazu (b). Dla niezbyt wysokich wartości ciśnienia (poniżej 2 MPa) oraz dla temperatur wyższych od temperatury wrzenia substancji, wpływ obu poprawek jest pomijalnie mały a opis stanu gazu równaniem Clapeyrona jest wystarczająco dokładny dla obliczeń inżynierskich.

Powyższe równania dotyczą konkretnej ilości gazów w układzie statycznym, np. w zamkniętym naczyniu lub pomieszczeniu. W praktyce przemysłowej, np. w przypadku wydalania gazów do atmosfery mamy do czynienia z objętościowym strumieniem gazów,
[m³/s], któremu odpowiada odpowiedni strumień molowy,
[kmol/s]. Objętościowy strumień gazów to określona jego objętość V, przepływająca przez element instalacji lub wydalana do atmosfery przez emitor w określonym czasie τ [s].

(1.17)

Równanie stanu gazu można również zastosować do strumieni gazów. Wzory (1.4) oraz (1.9) przyjmą wtedy odpowiednio postacie:

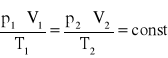
(1.18)

(1.19)

Dwa ostatnie wzory mają istotne znaczenie praktyczne. Służą do jednoznacznego określania wielkości strumienia emitowanych gazów. Wartość
zależy od parametrów gazów czyli od temperatury oraz ciśnienia (stąd za całkowicie poprawny zapis można uznać oznaczenie
), dlatego porównywanie różnych strumieni gazów ma sens wtedy gdy dokona się przeliczenia ich wartości na te same warunki odniesienia. Zwykle różne strumienie gazów, o różnych parametrach, pochodzące z różnych źródeł emisji lub z tego samego źródła ale w różnych fazach jego pracy, porównuje się po przeliczeniu na warunki normalne
.

Adaptując równanie (1.15) do opisu strumienia emitowanych gazów uzyskamy wzór pozwalający obliczać masowy strumień rozpatrywanego składnika m_i, którym może być np. zanieczyszczenie gazów. Jest do tego potrzebna znajomość jego prężności parcjalnej p_i.

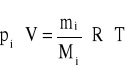
(1.20)

Do rozwiązania

Przykład 1.2

Określona ilość gazu zajmuje objętość
 = 2,20 m³ w temperaturze
 = 310 K i pod ciśnieniem
 = 0,993 ∙ 10⁵ Pa. Jaka będzie objętość tego gazu
w temperaturze
 = 291 K i pod ciśnieniem
 = 1,055 ∙ 10⁵ Pa.

Przykład 1.6

Jaka ilość gazu, wyrażona w kilomolach, mieści się w zbiorniku o objętości
 m³. Temperatura gazu jest równa
K a ciśnienie
Pa. Sprawdź jednostki.

Przykład 1.8

Jaka jest masa powietrza zawartego w pomieszczeniu o objętości V = 71,5 m³ jeśli temperatura wynosi T = 294 K a ciśnienie p = 1,006 ∙ 10⁵ Pa? Masa molowa powietrza zawartego w tym pomieszczeniu jest równa M_p = 28,9 kg/kmol. Sprawdź jednostki.

Przykład 1.10

Ciśnienie parcjalne ditlenku węgla w powietrzu wynosi
= 38,5 Pa. Jaka jego masa,
, mieści się w jednym metrze sześciennym powietrza, V = 1,00 m³, jeśli temperatura jest równa T = 297 K.

Przykład 2.11

W temperaturze
K i pod ciśnieniem
Pa jeden metr sześcienny powietrza, V = 1,00 m³, zawiera 7,44 grama pary wodnej,
kg. Jaką ilość pary wodnej,
będzie zawierał jeden metr sześcienny tego powietrza gdy temperatura wzrośnie do
K a ciśnienie pozostanie niezmienione?

Przykład 1.14

Strumień objętościowy gazów odlotowych wyzwalany w procesie produkcyjnym wynosi
 m³/s (tj. 18500 m³/h). Temperatura jest równa T₁ = 330 K a ich ciśnienie p₁ = 1,02 ∙ 10⁵  Pa. Określ wielkość strumienia gazów w przeliczeniu na warunki normalne,
.

Przykład 1.16

Do atmosfery jest wydalany strumień objętościowy gazów odlotowych
6,19 m³/s (tj.22300 m³/h). Temperatura gazów wynosi T = 331 K a ciśnienie jest równe
Pa. Gazy zawierają pary toluenu. Ciśnienie parcjalne par toluenu wynosi
Pa. Oblicz strumień masowy toluenu,
wydalany do atmosfery z gazami odlotowymi.

para

gaz

ciecz (woda)

Ciśnienie ,N/m²

612,9

273,1

T_K=647,1

ciało stałe (lód)

Punkt potrójny

Temperatura, K

---