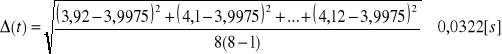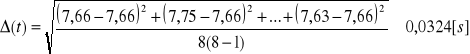1.Wstęp teoretyczny:
Ciecz doskonała:
Ciecz jednorodna, nielepka, nieściśliwa, a więc taką, której objętość nie zmienia się pod wpływem sił zewnętrznych (ciśnienia) nieprzewodząca ciepła, która nie paruje i nie zamarza; w cieczy doskonalej nie rozpuszczają się gazy; ciecz doskonała w przyrodzie nie występuje.
Wzór Stokesa:
Wzór określający siłę oporu R, która działa na kuliste ciało o promieniu r poruszające się z prędkością v w lepkiej cieczy: R=6πηrv, gdzie η - współczynnik lepkości; wzór Stokesa słuszny jest, gdy prędkość ciała jest dostatecznie mała (brak zawirowań cieczy) i służy m.in. do pomiaru lepkości cieczy; podany przez Stokesa 1851.
R=6πηrv
η-współczynnik lepkości cieczy
r- promień ciała
v-prędkość ciała
Ruchy kuli w cieczy:
Ruch laminarny:
W ruchu laminarnym tory cząstek różnią się niewiele od siebie. Pozostające w ruchu medium można traktować jako zbiór oddzielnych warstw, poruszających się względem siebie z różną prędkością i niemieszających się ze sobą. Ruch taki występuje w mediach o dużej lepkości (μ), np. lawa wulkaniczna.
Ruchu turbulentny:
W ruchu tym ruch cząstek płynu powoduje mieszanie się ze sobą rożnych warstw. Ruch ten występuje w mediach o względnie malej lepkości (μ), np. woda, powietrze. Przy niewielkich prędkościach strumienia ruch jest laminarny, a przy przekroczeniu pewnej prędkości granicznej przechodzi w ruch turbulentny. Istotą turbulencji są bezładne ruchy cząstek płynu, których wypadkowa wyznacza główny kierunek przepływu. Wielkość i kierunek wektora prędkości w danym punkcie zmienia się z chwili na chwilę, dlatego w ogólnym opisie ruchu burzliwego (turbulencji) operuje się prędkością średnią. Przekazywanie energii z jednej warstwy płynu do drugiej związane z obecnością zawirowań powoduje, że do efektów lepkości dynamicznej (μ), dołączają efekty tzw. lepkości wirowej, oznaczanej literą η (eta). W związku z tym wpływ turbulencji na transport materiału ziarnowego jest dwojaki, tj. lepkość wirowa zwiększa znacznie opór przepływu i naprężenia ściągające działające na dno. Obecność skierowanej pionowo ku górze składowej sił ciśnienia (składowej unoszącej) umożliwia unoszenie ziaren w zawiesinie. Istnienie siły unoszącej wyjaśnia równanie Bernoulli'ego.
Równanie Bernoulli'ego jest matematycznym zapisem zasady zachowania energii całkowitej w przepływie. Stosowane jest ono dla cieczy idealnych (doskonałych). W granicach dopuszczalnego błędu można je jednak stosować dla cieczy rzeczywistych. W ruchu turbulentnym siły wywierane przez znajdujący się w ruchu płyn na ziarno spoczywające na dnie mogą być, niezależnie od ich genezy, rozłożone na dwie składowe:
Siła skierowana równolegle do kierunku przepływu, zmierzająca do przemieszczenia ziarna po dnie, nazywana siłą wlekącą-

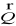

Siła skierowana prostopadle do kierunku przepływu, zmierzająca do poderwania ziarna w górę, nazywana siłą unoszącą.
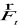
Zakłada się także, że wzdłuż linii prądu suma składników energii całkowitej w przepływie jest stała (Ecałk = const.), tzn. energia nie ulega zmianie w dół koryta, oraz przepływ Q jest również wielkością stałą (Q = const).
Ecałk = const
czyli: Ec = Ek + Ep + p
Ec - energia całkowita
Ek - energia kinetyczna
Ep - energia potencjalna
pV - energia związana z
ciśnieniem hydrostatycznym
p - ciśnienie hydrostatyczne
V - objętość
m - masa
g - przyśpieszenie siły ciężkości
h - wysokość n.p.m.
ς- gęstość
d - wysokość słupa wody (głębokość)
czyli:
przechodzimy do energii właściwej (Ewł)
= energii 1kg wody w dowolnym przekroju;
1kg wody=1dm3 czyli V=1
czyli:
/:ςg
Ewł - energia właściwa
v - prędkość
g - przyśpieszenie siły ciężkości
h - wysokość n.p.m., dla koryt o bardzo
małym nachyleniu praktycznie niezmienna
d - głębokość
zatem:
2. Wykonanie ćwiczenia:
Celem ćwiczenia był pomiar lepkości cieczy.
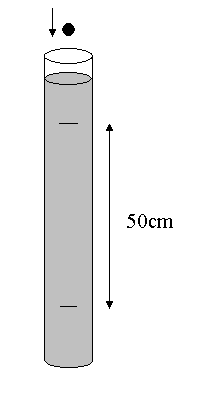
Schemat układu pomiarowego:
Układ pomiarowy składa się z rury szklanej wypełnionej cieczą, do której wrzucane są stalowe kulki.
Opis wykonania pomiarów:
Droga kulek jest liczona od pewnej odległości od powierzchni cieczy, ponieważ prędkość na początku nie jest stała. Średnica kulek była zmierzona mikromierzem, z czego został wyliczony je promień. Kulki były wrzucane tuż nad powierzchnią cieczy i możliwie jak najbliżej środka rury by odległość od ścian była jednakowa. Czas jest mierzony od momentu przekroczenia przez kulkę początku zaznaczonej drogi do odmierzonej odległości 50cm. Pomiary zostały wykonane w taki sam sposób dla 20 kulek.
Do doświadczenia użyto:
- rurę szklaną
- 16 szklanych kulek
- sekundomierz
- mikromierz
- 70% roztwór gliceryny
3. Tabelka z wynikami:
Nr |
l[m] |
d1[mm] |
t1[s] |
d2[mm] |
t2[s] |
|
|
|
1 |
0,855 |
10,47 |
3,92 |
6,47 |
7,66 |
0,529056 |
0,372175 |
|
2 |
|
|
4,1 |
|
7,75 |
0,55335 |
0,376548 |
|
3 |
|
|
4,03 |
|
7,76 |
0,543902 |
0,377034 |
|
4 |
|
|
4,01 |
|
7,6 |
0,541203 |
0,36926 |
|
5 |
|
|
3,98 |
|
7,67 |
0,537154 |
0,372661 |
|
6 |
|
|
3,98 |
|
7,55 |
0,537154 |
0,36683 |
|
7 |
|
|
3,84 |
|
7,67 |
0,518259 |
0,372661 |
|
8 |
|
|
4,12 |
|
7,63 |
0,556049 |
0,370717 |
|
|
|
|
3,9975 |
|
7,66125 |
0,539516 |
0,372236 |
|
4. Obliczenia:
Stałe wartości potrzebne do wykonania obliczeń:
Gęstość kulek: 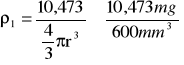
![]()
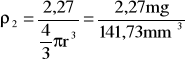
![]()
Stąd: ![]()
=![]()
, możemy stwierdzić, że oba rodzaje kulek są wykonane z tego samego materiału i mają taką samą gęstość.
Średnica rury: 2R = 5[cm] = 0,05[m]
Średnica d1 i d2: d1 = 10,47[mm] ≈ 0,01[m]
d2 = 6,47[mm] ≈ 0,006[m]
Gęstość cieczy: ![]()
Przyspieszenie ziemskie: ![]()
Wyznaczenie promienia kulki:
Obliczenie mikromierzem średnicy kulki d a następnie promienia r
![]()
np. ![]()
![]()
![]()
np. ![]()
![]()
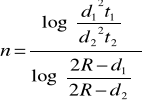
, gdzie d1-średnica dużych kulek w [m], d2- średnica małych kulek w [m], t1- czas opadania dużych kulek [s], t2-czas opadania małych kulek [s], 2R-średnica rury w [m].
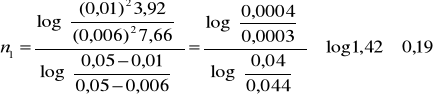
Analogicznie obliczamy pozostałe wartości n:
n2 = |
0,21 |
n3 = |
0,2 |
n4 = |
0,21 |
n5 = |
0,2 |
n6 = |
0,21 |
n7 = |
0,18 |
n8 = |
0,22 |
|
|
![]()
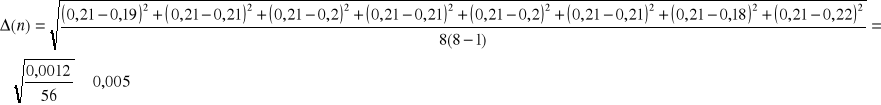
Obliczenie prędkości opadania kulki, ruch jest jednostajny, więc prędkość możemy obliczyć ze wzoru:
![]()
![]()
Obliczenie współczynnika lepkości ze wzoru:
![]()
Jednostki: 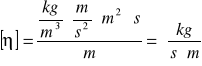
Np. 1) 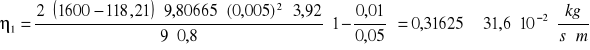
obliczane dla d1, analogicznie oblicza się dla pozostałych większych kulek.
2) 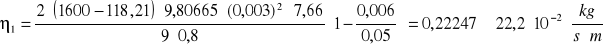
Obliczane dla d2, analogicznie oblicza się dla pozostałych mniejszych kulek.
Wyznaczenie średniej arytmetycznej współczynnika lepkości:
Dla d1:
![]()
Dla d2:
![]()
Analiza niepewności pomiarowych:
Błąd pomiaru czasu wynikający z dokładności sekundomierza i szybkości reakcji człowieka:
![]()
![]()
![]()
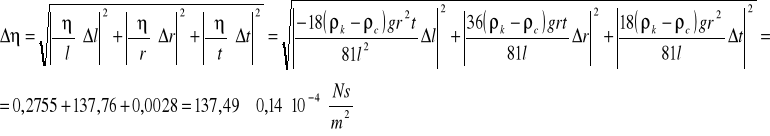
Podstawiając odpowiednie dane otrzymujemy ![]()
![]()
Obliczone dla d1.
Obliczone dla d2.
5. WNIOSKI:
Przed przystąpieniem do pomiarów musieliśmy zmierzyć i zważyć dwa rodzaje kulek.
Wrzucane kulki poruszały się z początku ruchem przyspieszonym, później jednak ich prędkość stabilizowała się. Aby uzyskać ruch jednostajny kulki i otrzymać poprawne wyniki pomiarów, rozpoczynaliśmy mierzenie czasu opadania kulki w odległości kilkunastu cm od tafli cieczy.
Niedokładność pomiaru może wynikać np. z niedoskonałej podziałki linijki (błąd systematyczny) lub błędów pomiaru czasu (niedokładne zmierzenie na sekundomierzu - błąd przypadkowy).
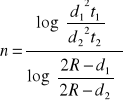
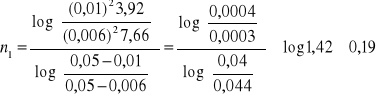
![]()
Wyszukiwarka
Podobne podstrony:
sprawozdanie 1, ZiIP, inne kierunki, politechnika, sem III, ergoom
sprawozdanie 5, ZiIP, inne kierunki, politechnika, sem III, ergoom
sprawozdanie 3, ZiIP, inne kierunki, politechnika, sem III, ergoom
materialoznastwo-sciaga, ZiIP, inne kierunki, politechnika, sem III, z pena
temat 13, ZiIP, inne kierunki, politechnika, sem III, ang
2, ZiIP, inne kierunki, politechnika, sem III, z pena, Downloads, materiały, spraw nowe
Finanse!, ZiIP, inne kierunki, politechnika, sem III, z pena
Materiałka, ZiIP, inne kierunki, politechnika, sem III, z pena
temat 6, ZiIP, inne kierunki, politechnika, sem III, ang
2, ZiIP, inne kierunki, politechnika, sem III, z pena, Downloads, materiały, spraw nowe
Tabela tygodnie parzyste-nieparzyste, ZiIP, inne kierunki, politechnika, sem III, z pena
Materiałoznawstwo - wstęp, ZiIP, inne kierunki, politechnika, sem III, z pena, Downloads, materialki
2, ZiIP, inne kierunki, politechnika, sem III, z pena, Downloads, materiały, spraw nowe
10 , ZiIP, inne kierunki, politechnika, sem III, z pena, Downloads, materiały, spraw nowe
temat 3, ZiIP, inne kierunki, politechnika, sem III, ang
temat 10, ZiIP, inne kierunki, politechnika, sem III, ang
więcej podobnych podstron