69. Definicja osi i wałów maszynowych. Klasyfikacja osi i wałów.

Osiami lub wałami nazywamy części służące do podtrzymywania ruchomych elementów maszynowych (przeważnie kół napędowych i innych), a same podparte w łożyskach.

Wałem nazywamy część, której głównym zadaniem jest przenoszenie momentu skręcającego.

Osie to tylko takie elementy, których zadaniem jest tylko podtrzymywanie elementów ruchomych. Oś nie przenosi w zasadzie momentu skręcającego.

Klasyfikacja osi i wałów:

- gładkie

- kształtowe - przekrój poprzeczny zmienny

Ze względu na sztywność:

- sztywne

- półsztywne

- giętkie

70. Obliczanie wytrzymałościowe osi ruchomych i nieruchomych

Osie obliczamy na ogół na zginanie. Po ustaleniu obciążenia zewnętrznego obliczamy reakcję łożysk osi. Następnie obliczamy moment gnący w przekroju niebezpiecznym. Jako naprężenia dopuszczalne w przypadku osi ruchomej k_go. W tym przypadku bowiem naprężenia we włóknach skrajnych zmieniają się od σ_gmax do σ_gmax. W przypadku osi nieruchomej bierzemy do obliczeń k_g lub k_gj , gdyż naprężenia nie mogą zmieniać tu znaku, a najwyżej wartość od 0 do σ_gmax. W pewnych przypadkach oś nieruchoma może być poddana obciążeniom zmiennym.

Warunek wytrzymałościowy:

skąd obliczamy średnicę osi:

lub

72. Obliczanie wału z warunku dopuszczalnych odkształceń skrętnych

Warunek wytrzymałości na skręcanie

moment skręcający

stąd średnicę wału można obliczyć ze wzoru

Wały długie ulegają znacznym odkształceniom skrętnym. Obliczanie cieńszych wałów uzależnia się często nie tylko naprężeń skręcających , ale i od dopuszczalnego kąta skręcania,

który wynosi 1/4^o na metr długości wału. Kąt skręcania wału możemy obliczyć ze wzoru

gdzie

l - oznacza długość odcinka skręcanego

G -moduł sprężystości postaciowej, którego wartość dla stali węglowej można przyjąć równą 810000 MN/m².

I_o - biegunowy moment bezwładności przekroju wału

ϕ=0,004 rad /m

rad /m

rad /m

71. Obliczanie wałów maszynowych dwupodporowych.

Wały dwupodporowe obliczamy na zginanie i skręcanie. W dowolnym przekroju wału panują naprężenia normalne wywołane zginaniem.

oraz styczne wywołane skręcaniem

naprężenia zastępcze

(1)

- przyjmujemy naprężenia zastępcze

gdzie zredukowane naprężenie

Przekształcając ten wzór następująco

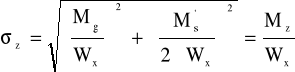
gdzie

możemy obliczyć tak zwany moment zastępczy

W przypadku jednoczesnych naprężeń zginających i skręcających obustronnie zmiennych, ważny będzie wzór (1) oraz wynikający z niego wzór na moment zastępczy.

Warunek wytrzymałości dla danego przekroju ma postać

stąd średnica danego przekroju dla wału pełnego

[cm]

dla wału drążonego uwzględniamy wartość wskaźnika wytrzymałości

73. Obliczanie wałów maszynowych wielopodporowych

Długie wały wielopodporowe stanowią one belki na wielu podporach jednocześnie skręcanie zginane. Ponieważ nie znamy z góry rozstawienia podpór, więc upraszczamy sobie zagadnienie obliczając je tylko na skręcanie. Przyjmujemy za to niższe naprężenia dopuszczalne . Obciążenie skrętne takich wałów może być co najwyżej tętniące. Bierzemy do obliczenia naprężenie k_sj zmniejszone o połowę. Ponieważ 0,5 k_sj = k_so, a więc do wzorów można zamiast k_sj wstawić k_so. Warunek wytrzymałości na skręcanie ma więc postać

74. Sprawdzenie sztywności statycznej i dynamicznej wałów, prędkość krytyczna.

Sztywność statyczna jest to właściwość wału polegająca na odkształcaniu się pod działaniem sił statycznych obciążających go. siłami tymi są przede wszystkim ciężary wirników oraz siły pochodzące od elementów współpracujących, a więc naciski na koła zębate, naciągi pasów w przypadku kół pasowych itp. Sprawdzenie sztywności polega na obliczeniu maksymalnego ugięcia wału (strzałki ugięcia) i sprawdzaniu, czy nie przekracza ona wartości dopuszczalnych dla danego typu maszyn.

Wzór określający strzałkę ugięcia ma postać:

gdy masa jest umieszczona w środku wału, to znaczy a = l/2 wtedy

Strzałka ugięcia wałów maszynowych nie powinna na ogół przekroczyć wartości:

f_dop = (0,0002 ÷ 0,0003) l

Ugięcia styczne wału:

Sztywnością dynamiczną wału określamy jako właściwość ulegania odkształceniom w warunkach ruchu wału.

Dynamiczne ugięcie wału:

Na masę m działa w płaszczyźnie prostopadłej do osi wału siła sprężystości ugiętego wału proporcjonalna od ugięcia y : S = k⋅y; przekładamy dla ośrodka masy siły d'Alamberta: B = m⋅y+e)⋅ω²

Siły te równoważą się: ky = m⋅(y+e)⋅ ω²

wyznaczamy stąd ugięcie dynamiczne y:

Stosunek k/m jest kwadratem częstości drgań giętych masy m na wale o sztywności k

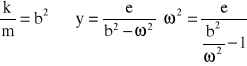
Współczynnik siły sprężystej k może być wyznaczony jako stosunek ciężaru wirnika do statycznej strzałki ugięcia

stąd częstość drgań giętych

Krytyczna prędkość kątowa wynosi:

ω_kr = b =

a krytyczna ilość obrotów

n_kr =

75. Klasyfikacja i cel stosowania sprzęgieł.

Cel stosowania.

Sprzęgła są to urządzenia, które służą do łączenia wałów. Stosuje się je wówczas, gdy np.

a) ze względu na znaczną długość, nie możemy użyć wału z jednolitego materiału, lecz z kilku odcinków (np. długie wały transmisyjne); mamy wówczas do czynnika ze sprzęgłami stałymi (sztywnymi)

b) zachodzi potrzeba okresowego odłączenia pewnych części wału, aby nie przenosiły ruchu np. w obrabiarkach, samochodach itp.; mamy wówczas do czynienia ze sprzęgłami wyłączalnymi

c) wały nie są współosiowe, lecz równoległe lub pochylone o pewien kąt (np. wał pędny samochodowy ze sprzęgłem Cardana); mamy wówczas do czynienia ze sprzęgłami okuwanymi lub przegubowymi

Klasyfikacja

a) sprzęgła sztywne

- sprzęgła tulejowe

- sprzęgła łubkowe

- sprzęgła tarczowe

b) sprzęgła samonastawne

- sprzęgła kołowe

- sprzęgła krzyżowe

- sprzęgła przegubowe

- sprzęgła zębate

- sprzęgła przegubowe zdwojone

- sprzęgła podatne

76. Sprzęgła sztywne i samonastawne - szkice.

Sprzęgła sztywne:

- tulejowe rys. 8.1

- łubkowe rys. 8.2

- tarczowe rys. 8.3, 8.4, 8.5

Sprzęgła samonastawne:

- kłowe rys. 8.8

- krzyżowe rys. 8.10

- przegubowe rys. 8.16

- zębate rys. 8.11

- przegubowe zwojowe rys. 8.17

- podatne rys. 8.32

77. Sprzęgła podatne, rodzaje charakterystyk, sztywność, współczynnik tłumienia - szkice

Jako sprzęgła podatne stosuje się przede wszystkim sprzęgła sprężyste. W sprzęgłach sprężystych między elementami łączącymi umieszczone zostają łączniki sprężyste Sprężyste ugięcia łącznika umożliwia pewną swobodę względnych odkształceń, w szczególności skrętnych

- sprzęgło tarczowe

tarcze łączone są ze sworzniami; sworznie połączone są z jedną tarczą sztywno, a z drugą za pośrednictwem krążków gumowych, skórzanych lub płóciennych

Sprzęgła podatne nierozłączne - sprzęgła kłowe mają one na swych tarczach występy (kły) zewnętrzne i wewnętrzne. Między kły wsunięte są skórzane klocki:

Specjalnym rodzajem sprzęgieł podatnych są sprzęgła zębate Na końcu wałów umieszczone są pierścienie z uzębieniem zewnętrznym Zęby te mają kształt łukowy i współpracują z

uzębieniem wewnętrznym umieszczonym w tulejach obejmujących wał. Takie wykonanie sprzęgła umożliwia przesunięcie względne wzdłużne oraz zmianę kąta pochylenia

osi wałów

Współczynnik tłumienia

78. Sprzęgła przegubowe - Cardana, szkice.

Do stałego łączenia wałów o osiach nie pokrywających się służą sprzęgła przegubowe (Cardana). Końce wałów zaopatrzone są w widełki, osadzone w sposób umożliwiający ich obrót na krzyżu K. Wały mogą ze sobą tworzyć kąt δ, który osiąga wartość do 30^o. wadą tych sprzęgieł jest niejednostajność prędkości kątowej ω₂ wały biernego. To niekorzystne zjawisko można usunąć przez zastosowanie dwóch sprzęgieł z wałkiem pośrednim, który powinien tworzyć jednakowych kąty z obu wałami.

79. Sprzęgła cierne, czas włączenia - szkice.

Sprzęgła cierne tarczowe - składa się z dwóch tarcz umieszczonych na końcach wałów i połączonych śrubami. Kołnierze mogą być odkute z wału, przyspawane do końca wału lub osadzone na nich skurczowo.

Najczęściej tarcze wykonane są oddzielnie i osadzone na wałach za pomocą klinów, wpustów, wieloklinów na stożek lub skurczowo. Dla środkowania tarcz stosuje się wytoczenia na płaszczyznach czołowych tarcz.

Sprzęgło tarczowe konstruujemy przy założeniu, że mement skręcający jest przenoszony tarcie między płaszczyznami czołowymi tarcz. Dla uzyskania koniecznej siły tarcia należy zaciskać tarczę śrubami z odpowiednią siła P_w.

Siła tarcia wynosi: T = P ⋅ μ

i powinna być równa sile wynikającej z momentu obrotowego

P_w ⋅ μ = P_z ⋅ μ =

stąd siła przypadająca na jedną śrubę

μ = 0,1 ÷ 0,2 - współczynnik tarcia

Czas włączania.

Moment rozruchu

M_r = M_t - M_o

wał napędzany osiągnie moment po czasie:

M_t - pełny moment tarcia, który utrzymuje się w ruchu

M_o - moment oporu wału napędowego

ω - prędkość kątowa

80. Sprzęgła hydrokinetyczne i elektromagnetyczne - szkice.

Sprzęgło elektromagnetyczne - włączane jest za pomocą elektromagnesu. Uzwojenia elektromagnesu (1) umieszczone sa w staliwnej tarczy (2), osadzonej zwykle na wale pędzącym. Tracza ta jest zaklinowana na wale. Prąd dopływa do uzwojenia za pośrednictwem izolowanych pierścieni (3). Druga tarcza (4) umieszczona jest przesuwnie na tulei (5) zaklinowanej na wale. Włączenie prądu powoduje przyciąganie tarczy przesuwnej i sprzęgnięcie wałów przez tarcie na powierzchniach pierścieni (6). Odsunięcie tarczy po włączeniu prądu następuje za pomocą sprężyn (7).

Sprzęgło hydrokinetyczne - stosowane do napędu pomp. Po stronie czynnej umieszczona jest pompo (1), po stronie biernej - turbina (2). Osłony (3) i (4) są złączone śrubami z tarczą czynną. Obejmuje ona część stałą nieruchomą (5), która może być łożyskiem wału biernego. W części tej umieszczony jest przewód (6). Przestrzeń między osłonami oraz wnętrza kanałów pompy i turbiny wypełnione są płynem. Przewód (6) i kanał (7) łączą przestrzeń między osłonami z kanałów pompy i turbiny. Przy obrocie wału czynnego pompa przepompowuje płyn na stronę bierną. Przepływ płynu powoduje obrót turbiny, a zatem i wału biernego. W sprzęgle tym występuje poślizg, czyli opóźnieni się wału biernego w stosunku do wału czynnego. Poślizg możemy regulować zmieniając ciśnienie płynu wypełniającego sprzęgło.

81. Porównanie łożysk ślizgowych i tocznych.

Łożyska toczne

Zalety

- mały współczynnik tarcia - niezależny od prędkości kątowej: 0,001 ÷ 0,003

- opory w czasie rozruchu prawie takie same jak dla ruchu ciągłego

- mniejsze zużycie smaru

- mniej wrażliwe na złe warunki smarowania

- małe wymiary wzdłużne, większe wymiary poprzeczne

- łatwa naprawa

- elementy znormalizowane, łatwo dostępne, znormalizowane według norm światowych

- małe koszty eksploatacji

Wady

- sztywność łożyskowania - duży hałas

- duże wymiary poprzeczne

- utrudniony montaż i demontaż wału

- duże koszty

- łożyska nie docierają się - duża dokładność montażu

Łożyska ślizgowe

---