Czy nie lepiej jako wynik pomiaru podać wartość średnią?

Ale jak określić jej niepewność - graniczny błąd przypadkowy?

Średnia wyników także zmienną losową, o odchyleniu standardowym

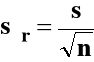
Zadania

1.Podać z prawdopodobieństwem 0.95 przedział wartości, w którym znajduje się rzeczywista wartość rezystancji jeśli odchylenie standardowe pomiaru wynosiło 0.1065Ω a w wyniku pomiaru uzyskano wartość 100.18Ω.

R= (100,18± 0,22)Ω

2.Podać z prawdopodobieństwem 0.95 przedział wartości, w którym znajduje się rzeczywista wartość rezystancji jeśli obliczony estymator odchylenia standardowego pomiaru s wynosił 0.1065Ω a średnia z 20 wyników pomiaru wynosiła 100.3485Ω.

ΔR=2*0.11/√20=0.0491 R=(100.35 ±0.05) Ω

3.Jak zmieni się wartość niepewności jeśli wymagać będziemy, że z prawdopodobieństwem 0,997 błąd przypadkowy wyniku jest nie większy od obliczonej niepewności. Podaj wynik pomiaru.

W praktyce liczba powtórzeń pomiarów w tych samych warunkach wynosi kilka, kilkanaście do kilkudziesięciu - źle oszacowany estymator odchylenia średniokwadratowego s. Dlatego przy małej liczbie pomiarów do określenia wartości błędu przypadkowego stosujemy tzw rozkład t- Studenta

Czy estymator s obliczony z małej liczby wyników pomiarów jest raczej „zaniżony” czy „zawyżony”?

Jeśli w serii pomiarowej jeden wynik znacznie różni się od pozostałych skłonni jesteśmy zakładać, że wynik ten pochodzi z jakiejś naszej omyłki. Jak w takim wypadku postępować?

Ograniczymy się do intuicji

BŁĘDY W POMIARACH BEZPOŚREDNICH I POŚREDNICH

POMIAR BEZPOŚREDNI - wynik pomiaru odczytany wprost z przyrządu, systemu.

ANALIZA - usunięcie z wyniku surowego błędów systematycznych, oszacowanie błędów przypadkowych, usunięciu błędów nadmiernych, określenie błędu narzędzia pomiarowego

X_s - wynik surowy

ΔX_s=ΔX_p+ΔX_syst+ΔX_przyp

ΔX_s- błąd wyniku surowego

ΔX_p- błąd pochodzący z ograniczonej dokładności

przyrządu

ΔX_syst - błąd systematyczny

ΔX_przyp -graniczny błąd przypadkowy (niepewność przypadkowa)

Jeśli ΔX_syst nie jest pomijalnie małe to WYNIK POMIARU należy POPRAWIĆ.(Co to znaczy pomijalnie mały?)

X= X_s - ΔX_syst =X_s + p

p-poprawka p=- ΔX_syst

Pozostałe składowe błędu ΔX_p i ΔX_przyp decydować będą o błędzie granicznym wyniku ( o niepewności wyniku)

ΔX_p- błąd graniczny przyrządu (niepewność pochodząca od przyrządu)

ΔX_przyp - graniczny błąd przypadkowy (niepewność przypadkowa) określony najczęściej z prawdopodobieństwem 0,997 (na poziomie ufności 0,003; poziom ufności 1- p; 1-0,997=0,003)

Sumaryczny błąd graniczny można zapisać następująco:

ΔX=±(|ΔX_p|+|ΔX_przyp |+|ΔX_{reszta system}|)

gdzie |ΔX_{reszta system}| „nieusuwalna” część błędu systematycznego Można się spodziewać, że |ΔX_{reszta system}| <<ΔX_syst

Jeśli wartość błędu granicznego przyrządu ΔX_p jest o rząd

większa od sumy pozostałych błędów

|ΔX_p||≥ 10*(|ΔX_przyp |+|ΔX_{reszta system}| )

można zaniedbać (|ΔX_przyp |+|ΔX_{reszta system}| )

wtedy X_rzecz ∈ < X-ΔX_p, X+ΔX_p >

Przyjmuje się, że można zaniedbać składowe pomijalnie małe - czyli składowe co najmniej 10-krotnie.

Pytania.

Czemu w pomiarach należy unikać dużych błędów systematycznych?

Czy zawsze możemy dokładnie określić błąd systematyczny, jaka niepewność określenia poprawki i jak wpływa na błąd graniczny wyniku pomiaru?

Wróćmy do przykładu bezpośredniego pomiaru prądu w obwodzie o szacowanej rezystancji, w którym uznaliśmy, że wynik pomiaru należy poprawić.

I_x=I_A + p

Wynik zapisano jako I_x=(I_A + p) ± ΔI_A

Ale poprawka określona także z pewną niepewnością Δp

Istotny stosunek ΔI_A do Δp

Δp - ΔX_{reszta system}

POMIAR POŚREDNI, ZŁÓŻONY

Pomiar pośredni - pomiar , w którym wielkość mierzona określana z zależności funkcyjnej wiążącej wielkość mierzoną pośrednio z wielkościami mierzonymi bezpośrednio.

Pomiar złożony - w czasie pomiaru konieczna zmiana warunków pomiaru

MUSI BYĆ ZNANA FUNKCJA WIĄŻĄCA WIELKOŚĆ MIERZONĄ „y” Z WIELKOŚCIAMI MIERZONYMI BEZPOŚREDNIO x₁..... x_i

y=f(x₁..... x_i)

Co rozumiemy przez obliczenie funkcji y jeśli argumentami wyniki pomiarów x_i±Δ x_i ?

Należy znaleźć y±Δ y

Szukamy przedziału y_Rz ∈ < y - Δ y , y + Δ y >

zawierającego wartość rzeczywistą y_Rz ,gdy argumenty funkcji przyjmują wartości z przedziału

x_i ∈ <x_iz - Δ x_i , x_iz + Δ x_i >

x_iz = x_izmierz

Wynik pomiaru x_i - środek przedziału, w którym mieści się z dużym prawdopodobieństwem wartość rzeczywista, a niepewność wyniku (błąd graniczny) to połowa tego przedziału.

Według tej samej definicji powinniśmy określić wynik pomiaru pośredniego (złożonego)

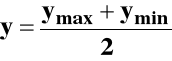
a błąd pomiaru - połowa przedziału

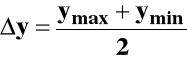
błąd powinien być -

Δy Δy

y_min y y_max

Rozpatrzmy przykład funkcji liniowej

y= a₀ +a₁x₁+a₂x₂+a₃x₃+.........+ a_ix_i

a₀,....a_i- liczby rzeczywiste dodatnie,

x₁.....x_i- wyniki pomiarów bezpośrednich obarczone błędem granicznym ±Δ x_i

y_max = f(x)_max = a₀ + a₁(x₁+Δx₁) + (x₂+Δx₂) + (x₃+Δx₃) +.........+ (x_i+Δx_i)

y_min = f(x)_min = a₀ + a₁(x₁−Δx₁) + (x₂−Δx₂) + (x₃−Δx₃) +...........+ (x_i−Δx_i)

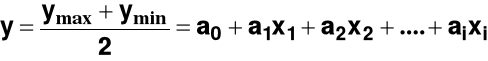
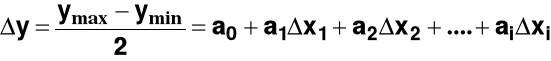
usunąć a₀

1. Określ przedział wartości, w którym znajduje się rzeczywista wartość rezystancji wypadkowej R_x = 5342Ω trzymanej w wyniku połączenia szeregowego oporników: 1kΩ kl 0,05; 100Ω kl 0,05; 10Ω kl 0,05; 1Ω kl 0,1 (klasa rezystora to maksymalny błąd względny określenia wartości nominalnej rezystancji wyrażony w procentach;

1kΩ kl 0,05 =1kΩ ±0,05%=1kΩ ± 0.5Ω).

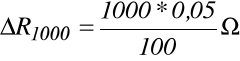
2. Podaj wynik pomiaru mocy prądu P=I*U stałego wydzielanej na rezystorze, jeśli wiadomo, że napięcie na rezystancji wynosiło U_R=10,00V ± 0,05V (0,5%), a prąd płynący przez nią I_R= 200mA ± 1mA (0,5%).

P=10V*200mA+1mA*0,05V =2000mW+0,05mW

ΔP=10V*1mA+200mA*0,05V=2 mW

P=2000mW±20mW

Jeśli funkcja wiążąca wielkość mierzoną pośrednio z wielkościami mierzonymi bezpośrednio jest uwikłana to znalezienie minimum i maksimum funkcji kłopotliwe.

ALE

Jeśli funkcja Y=f(X₁......... X_N) jest różniczkowalna i w przybliżeniu liniowa w obszarze określonym przez wyniki pomiaru (X₁......... X_N) to:

za wynik pomiaru można przyjąć wartość funkcji obliczoną z

zależności:

Y=f(X₁......... X_N)

gdzie X_i - wyniki pomiarów bezpośrednich

a graniczny błąd bezwzględny pomiaru wyznaczyć metodą różniczki zupełnej

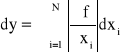
przypisując wartościom różniczek wartości błędów dx_i = ΔX_i

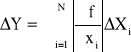
- pochodna funkcji przy założeniu, że zmienną w funkcji f jest x₁, a pozostałe (x₂..... x_i) traktujemy jako stałe.

Błąd względny

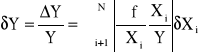
Przykłady

y= a₀ +a₁x₁+a₂x₂+a₃x₃+.........+ a_ix_i

∂y dy

∂x₁ dx₁ różniczkując po x₁ traktujemy pozostałe zmienne x₂, x₃, x_n jak stałe

∂y dy dy_(x1) =a₁dx₁ dy_(x2) =a₂dx_{2 .........}

∂x₁ dx₁ dx₁=Δx₁ d x₂ =Δx₂

Δy_(x1) =a₁Δx₁ Δy_(x2) =a₂Δx₂

Δy= a₁Δx₁+a₂Δx₂+a₃Δx₃+.........+ a_iΔx_i = Σa_iΔx_i

y = x₁ + x₂ dy =dx₁+ dx₂

Δy =Δx₁+ Δx₂

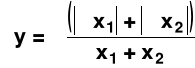
y = x₁ − x₂ dy =dx₁+ dx₂

Δy =Δx₁+ Δx₂

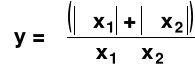
Jeśli wielkość y mierzona pośrednio jest sumą lub różnicą wielkości mierzonych x bezpośrednio to

błąd BEZWZGLĘDNY Δy jest sumą błędów BEZWZGLĘDNYCH wielkości x

y = x₁*x₂ dy= dx₁*x₂ +dx₂*x₁

Δy= Δx₁*x₂ +Δx₂*x₁

δy =±( δx₁+δx₂)

y = x₁/x₂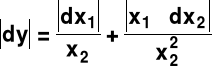

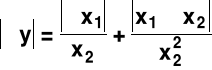
δy =±( δx₁+δx₂)

Jeśli wielkość y mierzona pośrednio jest iloczynem lub ilorazem wielkości mierzonych x bezpośrednio to

błąd WZGLĘDNY δy jest sumą błędów WZGLĘDNYCH wielkości x

Przy dużej liczbie zmiennych

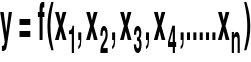
błąd graniczny liczony w ten sposób jest mało prawdopodobny. Mało prawdopodobne że wszystkie wielkości mierzone są obarczone maksymalnymi błędami granicznymi.

Dla dużej liczby zmiennych (wyników pomiaru) jeśli można założyć, że błędy są niezależne zamiast GRANICZNEGO BŁĘDU podaje się tzw BŁĄD STATYSTYCZNY , którego wartość określa się z zależności

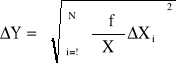
Możemy powiedzieć, że z dużym prawdopodobieństwem błąd nie przekroczy wartości obliczonej na podstawie powyższego wzoru a na pewno nie będzie większy od

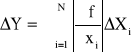
(pod warunkiem poprawnego określenia błędów składowych)

Zadania:

1. Określić niepewność wyniku pomiaru R , jeśli rezystancję zmierzono w oparciu o prawo Ohma. Napięcie na oporniku wynosiło 14,35V±0,03V a prąd płynący przez opornik 32,14mA±0,03mA

2. Napięcie Ex jest różnicą napięcia wzorcowego Ew=1,0000V±0,0001V i napięcia wskazywanego przez miliwoltomierz U_v=25,2mV± 0,5mV.Podaj wartość Ex oraz graniczną niepewność względną i bezwzględną podanego wyniku.

3. Jak zmieniłaby się wartość niepewność względnej i bezwzględnej gdyby określano je na podstawie mniej ostrych kryteriów ( na podstawie założenia o normalnym rozkładzie błędów i rozumowaniu statystycznym)?

4. Metodą statystyczną można obliczać błędy pomiarów pośrednich:

1. gdy wyniki obarczone niepewnościami przypadkowymi,

2. gdy wyniki obarczone niezależnymi błędami granicznymi,

3. zawsze gdy liczba zmiennych , z których obliczamy wielkość mierzoną y jest większa od 5.

wykład 3/IF 8

---