ŹRÓDŁA BŁĘDÓW, CHARAKTER BŁĘDÓW - BŁĘDY SYSTEMATYCZNE I PRZYPADKOWE.

Źródła błędów:

1. ograniczona dokładność* narzędzi pomiarowych,

2. zły model obiektu,

3. niewłaściwy przyrząd (nie mierzy poprawnie badanej cechy),

4. wpływ przyrządu na obiekt mierzony,

5. niestarannie zestawiony układ pomiarowy,

6. niekontrolowany wpływ czynników zewnętrznych na przyrząd,

7. zakłócenia wielkości mierzonej ( wpływ czynników zewnętrznych na badany obiekt),

8. ..............

*Dokładność narzędzi pomiarowych - właściwość określająca zdolność do dawania wyników bliskich wartości rzeczywistej.

JAK wykryć obecność błędów - jak oszacować niepewność wyniku?

CHARAKTER BŁĘDÓW

BŁĘDY SYSTEMATYCZNE, BŁĘDY PRZYPADKOWE

BŁĘDY SYSTEMATYCZNE to błędy, które przy wielu pomiarach tej samej wartości wielkości mierzonej, wykonywanych w tych samych warunkach, pozostają stałe lub zmieniają się według określonego prawa wraz ze zmianą warunków .

Przykładowe źródła błędów systematycznych :

- Oddziaływanie przyrządu na obiekt mierzony

naruszenie równowagi energetycznej obiektu - błąd metody

przykłady:

• pomiar temperatury termometrem kontaktowym,(zmieniamy warunki chłodzenia, tym samym temperaturę mierzoną)

• pomiar małej rezystancji po dołączeniu jej do układu pomiarowego dwoma długimi przewodami,

• zmiana prądu w obwodzie spowodowana włączeniem amperomierza o niezerowej rezystancji.

- Niedokładność miary wzorca, błąd wzorcowania przyrządu

przykłady :

• uproszczenie modelu, konstrukcji, np założenie liniowości podziałki,

• niedoskonałość wykonania,

- Zmiany warunków pomiaru w stosunku do wymaganych

warunków odniesienia - błąd dodatkowy

przykład : zmiana parametrów narzędzia- wydłużenie długości taśmy mierniczej

wraz ze zmianą temperatury

BŁĘDY SYSTEMATYCZNE

Trudne do ujawnienia, wymagają od pomiarowca wnikliwości, znajomości

obiektu, zasad działania aparatury,

NIEBEZPIECZNE - niezauważone mogą bardzo zniekształcać

wyniki.

Jeśli potrafimy zauważyć i oszacować ΔX_sys można go usunąć z wyniku

pomiaru, poprawić „surowy” wynik X_zmierz i przyjąć za wartość zmierzoną

X_{zmierz. poprawione}

Przyjęliśmy definicję błędu ΔX= X_zmierz - X

w tej konwencji zapisu ΔX_sys= X_zmierz - X_{zmierz. poprawione}

stąd X_{zmierz. poprawione} = X_zmierz - ΔX_sys

Często używa się pojęcia poprawka

POPRAWKA - to błąd systematyczny z przeciwnym znakiem

P = - ΔX_sys

Poprawiony wynik pomiaru X= X_zmierz- ΔX_sys= X_zmierz+ p

Czy tak określony wynik nie jest już obarczony żadnym błędem, jest

wartością pewną?

Zadania

1. W obwód pomiarowy o rezystancji około 1000Ω włączono amperomierz o rezystancji 10Ω, który wskazał I_A = 14.53 mA. Błąd graniczny wskazań amperomierza (niepewność wskazań amperomierza) wynosi ±0,02mA.


Jaki błąd względny i bezwzględny popełnimy jeśli nie zauważymy, że włączenie amperomierza zmieniło prąd w obwodzie? Jak należy podać wynik pomiaru?

2. Rezystancja połączenia mierzonych oporników z układem pomiarowym była nie większa niż 15mΩ;

W pomiarze jakich wartości rezystancji błąd pochodzący od nieuwzględnienia „doprowadzeń” miałby wartość nie większa niż 0,1%?

Czy zawsze można dokładnie określić wartość błędu systematycznego i usunąć go z wyniku ?

BŁĘDY PRZYPADKOWE

Mogą być ujawnione poprzez powtarzanie pomiaru .

Jeśli w pozornie takich samych warunkach pomiaru zmieniają się wyniki to odpowiedzialne są za to błędy przypadkowe.

Przykładowe przyczyny:

• histereza wskazań,

• szumy termiczne,

• nieuwaga obserwatora,

• krótkotrwałe zmiany warunków zewnętrznych niezauważone przez obserwatora,

• niestaranny pomiar, niestarannie wykonany układ pomiarowy,

• błąd modelu, itp.

W jaki sposób uwzględnić w zapisie wyniku niepewność mającą swe źródło w błędach przypadkowych?

Co jest najlepszą miarą wielkości mierzonej i jaka jest jej niepewność?

W wyniku pięciokrotnego pomiaru rezystancji R_X uzyskano następujące wyniki:

100,12Ω

100,14Ω

100,06Ω

100,11Ω

100,08Ω

Jakie jest najlepsze przybliżenie wartości R_X ?

Wartość średnia

Ogólnie wartość średnia

stosowany zapis

Co przyjąć za miarę błędu?

Różnicę między wartością zmierzoną a wartością średnią ?

X_i - X_śr

Różnica ta często nazywana jest odchyleniem od wartości średniej.

Czy wartość średnia odchyleń może być miarą niepewności przypadkowej?

Obliczanie odchyleń
Nr pomiaru	wartość zmierzona	odchylenie d=Ri - Rśr
1	100,12	0,018
2	100,14	0,038
3	100,06	-0,042
4	100,11	0,008
5	100,08	-0,022
średnia	100,102	0,00

Wartość średnia odchyleń = 0

Co przyjąć za miarę niepewności ?

Podnieść do kwadratu odchylenia i obliczyć odchylenie średniokwadratowe - odchylenie standardowe.

Obliczanie kwadratów odchyleń
Nr pomiaru	wartość zmierzona	odchylenie d=Ri - Rśr	d*d
1	100,12	0,018	0,000324
2	100,14	0,038	0,001444
3	100,06	-0,042	0,001764
4	100,11	0,008	6,4E-05
5	100,08	-0,022	0,000484
średnia	100,102	0,00	0,00408

Odchylenie średniokwadratowe - odchylenie standardowe

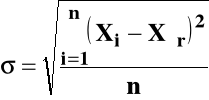
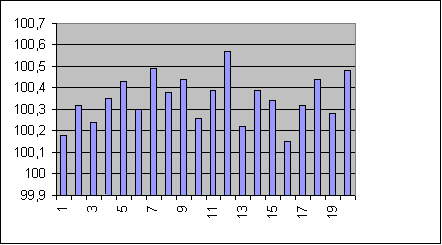
Rozpatrzmy liczniejszą serię wyników pomiaru

i	R		R -Rśr	(R-Rśr)*(R-Rśr)
1	100,18		-0,1685	0,02839
2	100,32		-0,0285	0,00081
3	100,24		-0,1085	0,01177
4	100,35		0,0015	0,00000
5	100,43		0,0815	0,00664
6	100,3		-0,0485	0,00235
7	100,49		0,1415	0,02002
8	100,38		0,0315	0,00099
9	100,44		0,0915	0,00837
10	100,26		-0,0885	0,00783
11	100,39		0,0415	0,00172
12	100,57		0,2215	0,04906
13	100,22		-0,1285	0,01651
14	100,39		0,0415	0,00172
15	100,34		-0,0085	0,00007
16	100,15		-0,1985	0,03940
17	100,32		-0,0285	0,00081
18	100,44		0,0915	0,00837
19	100,28		-0,0685	0,00469
20	100,48		0,1315	0,01729
Rśr	100,3485		0	0,01134	średnia kwadratów R-Rśr
Rmax	100,57			0,10650	pierwiastek z średniej
Rmin	100,15				kwadratów "odchyleń" (R-Rśr)
σ	0,1065
σśredn.	0,0238

Uporządkowane wyniki

R		przedział wartości	liczba obserwacji	częstość
100,15		100,15 - 100,19	2	0,1
100,18		100,20 -100,24	2	0,1
100,22		100,25 - 100,29	3	0,15
100,24		100,30- 100,34	4	0,2
100,26		100,35 -100,39	4	0,2
100,28		100,40 -100,44	3	0,15
100,3		100,45 -100,49	2	0,1
100,32		100,50 -100,54	0	0
100,32		100,55 -100,59	1	0,05
100,34		przedział wartości	liczba obserwacji	częstość
100,35		100,15 - 100,24	4	0,20
100,38		100,25 -100,34	6	0,30
100,39		100,35 - 100,44	7	0,35
100,39		100,45 - 100,54	2	0,10
100,43		100,55 -100,64	1	0,05
100,44		przedział wartości	liczba obserwacji	częstość
100,44			2	0,10
100,48		100,20 - 100,29	4	0,20
100,49		100,30 - 100,39	7	0,35
100,57		100,40 - 100,49	5	0,25
100,3485		100,50 - 100,59	1	0,05

Graficzne przedstawienie rozkładu wyników pomiaru nazywamy HISTOGRAMEM.

Oś x - cały przedział wartości, w którym mieszczą się wyniki pomiaru podzielony na „podprzedziały”

Oś y - częstość występowania wyniku w kolejnym „podprzedziale”

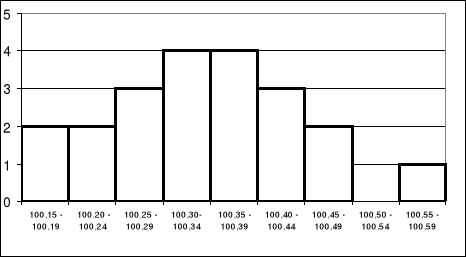
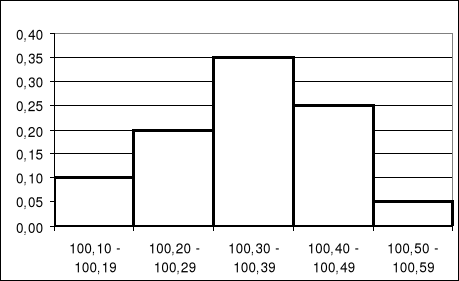
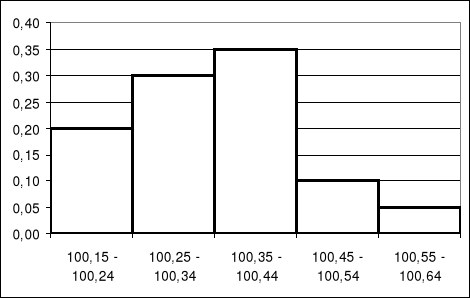
Jak zmieni się kształt histogramu jeśli pomiary obarczone będą mniejszym błędem przypadkowym , a nie zmienimy skali osi x?

Jak zmieniać się będzie kształt histogramu w miarę wzrostu liczby wyników obarczonych błędami przypadkowymi?

Kształt histogramu zbliżać się będzie (prawie zawsze) do symetrycznej krzywej dzwonowej. Funkcja matematyczna opisująca tą krzywą nosi nazwę funkcji rozkładu normalnego lub funkcji Gaussa.

Wyniki pomiarów obarczonych błędami przypadkowymi można potraktować jako zmienne losowe niezależne opisane funkcja Gaussa.

Znormalizowana funkcja opisująca rozkład normalny ma postać

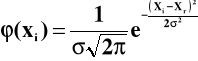
x_i - zmienna losowa - wynik pomiaru

Δ x_i = x_i - x_r

Δ x_i - błąd przypadkowy pomiaru - zmienna losowa o takim samym rozkładzie jak x_i -

ϕ(x_i) ⇒ f(x_i - x_r) = f(Δ x_i)

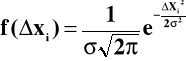
Właściwości :

• duży błąd jest mniej prawdopodobny niż błąd mały,

• błędy równe co do modułów są jednakowo prawdopodobne,

• dla dostatecznie dużych błędów Δx f(Δx) ⇒ 0,

MIARĄ PRAWDOPODOBIEŃSTWA uzyskania wyniku obarczonego błędem z przedziału (Δx₁, Δx₂) jest pole pod krzywą.

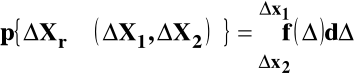
Prawdopodobieństwo, że

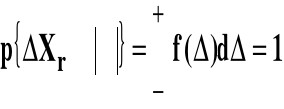
Parametr charakteryzujący rozkład -
ODCHYLENIE STANDARDOWE (dyspersja, błąd średniokwadratowy)

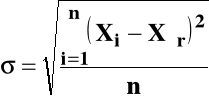
jeśli σ rośnie , krzywa staje się szersza - rośnie prawdopodobieństwo pojawienia się większych błędów.

_+σ

p{Δx_r≤ σ}= ∫ f(Δ)dΔ =0,68

^-σ

` p{Δx_r≤ σ}= 0,68

oznacza, że z prawdopodobieństwem 0,68 wartość rzeczywista pojedynczego wyniku pomiaru nie różni się od wartości rzeczywistej więcej niż o Δx = ±σ

(68% wyników obarczonych jest błędem nie większym niż σ, ale 32% błędem większym)

Takie prawdopodobieństwo na ogół nie satysfakcjonuje pomiarowca, Jeśli chcemy mieć „większą pewność”, że poprawnie określono przedział wartości, w którym znajduje się wartość rzeczywista wielkości mierzonej to musimy dopuścić większy błąd.

Z rozkładu normalnego wynika, że 95,4% krzywej znajduje się w obszarze ±2σ

p{Δx_r≤2σ}= 0,95

p{Δx_r≤ 3σ}=0,997

Ponieważ nie znamy wartości rzeczywistej , możemy tylko estymować wartość rzeczywistego odchylenia standardowego zastępując wartość rzeczywistą jej najlepszym oszacowaniem czyli wartością średnią.

s= estymator σ

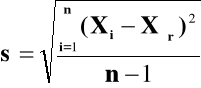
p{Δx_r≤2s}= 0,95 p{Δx_r≤ 3s}=0,997

Czy nie lepiej jako wynik pomiaru podać wartość średnią?

--------------------------

Ale jak określić jej niepewność - graniczny błąd przypadkowy?

i	R			i	R
1	100,18			1	100,18	100,39
2	100,32			2	100,32	100,57
3	100,24			3	100,24	100,22
4	100,35			4	100,35	100,39
5	100,43			5	100,43	100,34
6	100,3			6	100,3	100,15
7	100,49			7	100,49	100,32
8	100,38			8	100,38	100,44
9	100,44			9	100,44	100,28
10	100,26			10	100,26	100,48
11	100,39			Rśr	1003,390	1003,580
12	100,57			Rmax	100,49	100,57
13	100,22			Rmin	100,18	100,15
14	100,39			s	0,0929	0,1178
15	100,34			sśr	0,0294	0,0373
16	100,15
17	100,32
18	100,44
19	100,28
20	100,48
Rśr	2006,970
Rmax	100,57
Rmin	100,15
s	0,1065
sśr	0,0238

Średnia wyników także zmienną losową, o odchyleniu standardowym

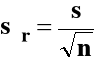
Zadania

1.Podać z prawdopodobieństwem 0.95 przedział wartości, w którym znajduje się rzeczywista wartość rezystancji jeśli odchylenie standardowe pomiaru wynosiło 0.11Ω a w wyniku pomiaru uzyskano wartość 100.18Ω.

R= (100,18± 0,22)Ω

2.Podać z prawdopodobieństwem 0.95 przedział wartości, w którym znajduje się rzeczywista wartość rezystancji jeśli obliczony estymator odchylenia standardowego pomiaru s wynosił 0.11Ω a średnia z 20 wyników pomiaru wynosiła 100.3485Ω.

ΔR=2*0.11/√20=0.0491 R=(100.35 ±0.05) Ω

3.Jak zmieni się wartość niepewności jeśli wymagać będziemy, że z prawdopodobieństwem 0,997 błąd przypadkowy wyniku jest nie większy od obliczonej niepewności. Podaj wynik pomiaru.

W praktyce liczba powtórzeń pomiarów w tych samych warunkach wynosi kilka, kilkanaście do kilkudziesięciu - źle oszacowany estymator odchylenia średniokwadratowego s. Dlatego przy małej liczbie pomiarów do określenia wartości błędu przypadkowego stosujemy tzw rozkład t- Studenta

Czy estymator s obliczony z małej liczby wyników pomiarów jest raczej „zaniżony” czy „zawyżony”?

PARAMETR ROZKŁADU t -STUDENTA t_np

ΔX = t_np. * S

Wartość współczynnika t_np. zależy od liczby obserwacji n i wymaganego

prawdopodobieństwa p.

Wybrane wartości współczynnika t_np dla p=0,95

n	2	4	6	8	10	12	20	30
tnp	4.307	2.776	2.477	2.306	2.228	2,129	2.089	2.042

Zadanie

Podać z prawdopodobieństwem 0.95 przedział wartości, w którym znajduje się rzeczywista wartość rezystancji jeśli obliczony estymator odchylenia standardowego pomiaru s wynosił 0.1065Ω a średnia z 20 wyników pomiaru wynosiła 100.3485Ω.

ΔR=2,089*0.1065/√20=0.04974 R=(100.35 ±0.05) Ω

Podać z prawdopodobieństwem 0.95 przedział wartości, w którym znajduje się rzeczywista wartość rezystancji jeśli obliczony estymator odchylenia standardowego pomiaru s wynosił 0.092 Ω a średnia z 10 wyników pomiaru wynosiła 100.339 Ω.

ΔR=2,228 *0.092/√10=0.06481 R=(100.34 ±0.07) Ω

Pytania

1.Wielokrotne powtarzanie pomiaru w tych samych warunkach pozwala na zauważenie błędu :

1. przypadkowego,

2. systematycznego,

3. nadmiernego,

2.Błędy przypadkowe :

1. dodatnie są tak prawdopodobne jak ujemne,

2. błędy duże są bardziej prawdopodobne niż małe,

3. odchylenie standardowe średniej jest n -krotnie mniejsze niż odchylenie standardowe pojedynczego wyniku.

3. Współczynnik, przez który należy przemnożyć odchylenie standardowe :

1. zależy od żądanego prawdopodobieństwa, że wartość rzeczywista leży w wyznaczonym przedziale wartości,

2. dla krótkiej serii określany powinien być z rozkładu t- Studenta,

3. współczynnik ten dla rozkładu t- Studenta jest większy niż dla rozkładu Gaussa.

Wykład2 / miernictwo elektroniczne- IF 12

---