PÓŁPRZEWODNIKI

Nazwa tych materiałów wynika z pośredniej - w porównaniu z dobrymi przewodnikami i dobrymi izolatorami - oporności właściwej. Dla najlepszych przewodników (miedź, srebro) wynosi ona ok. 1,6÷1,7·10^-8 Ω·m, podczas gdy dla najlepszych izolatorów przekracza nawet 10¹⁶ Ω·m. Do półprzewodników zalicza się materiały o oporności właściwej od 10^-6 Ω·m do 10⁺⁸ Ω·m, bardziej jednak istotny jest inny niż w metalach mechanizm przewodnictwa. W przewodnikach jest dużo swobodnych elektronów (w metalach 1-2 na każdy atom), w izolatorach nie ma ich w ogóle - tzn. są silnie związane w swoich macierzystych atomach; natomiast w półprzewodnikach elektrony są słabo związane ze swoimi atomami i pod wpływem odpowiedniego pobudzenia mogą się uwolnić. W uproszczeniu: cokolwiek zrobimy z metalem, i tak przewodzi; cokolwiek zrobimy z izolatorem, i tak nie przewodzi; półprzewodniki przewodzą zaś lub nie przewodzą zależnie od słabych bodźców, można je włączać i wyłączać, i stąd wynika ich ogromna rola w elektronice.

Aby objaśnić dokładniej mechanizm przewodnictwa elektrycznego w ciałach stałych, musimy powołać się na teorię pasm energetycznych. Jak wiadomo z fizyki szkolnej (por. model Bohra atomu wodoru), elektron w pojedynczym atomie może występować tylko w jednym z dozwolonych stanów związanych (na jednej z dozwolonych orbit). Jeśli odłożymy energię na osi pionowej, to każdemu takiemu stanowi odpowiada linia pozioma - stąd mówimy o poziomach energetycznych. Swobodny (nie związany z jądrem atomu) elektron może natomiast mieć dowolną energię kinetyczną E = mv²/2. Właściwości elektronu w krysztale są pośrednie między dwoma tymi przypadkami, gdyż może się on poruszać w całej objętości kryształu, pozostając jednak pod wpływem przyciągającego oddziaływania jąder. Dlatego i struktura poziomów energetycznych wykazuje cechy pośrednie: każdy z poziomów energetycznych występujących dla pojedynczego atomu ulega poszerzeniu, przechodząc w pasmo, składające się z ogromnej liczby bardzo blisko leżących poziomów; stany należące do danego pasma różnią się wartością prędkości elektronu i kierunkiem jego ruchu.

Tak jak w pojedynczym atomie, w krysztale również kolejne elektrony zapełniają stany od najniższej energii w górę. Pasma całkowicie wypełnione nie dają przy tym wkładu do przewodnictwa, gdyż mamy w nich tyle samo elektronów poruszających się z dodatnim, co z ujemnym zwrotem wzdłuż dowolnej osi, tak że „netto” nie następuje przepływ ładunku. Aby nastąpił przepływ prądu, więcej elektronów musi zajmować stany odpowiadającego ruchowi w pewnym wyróżnionym kierunku, podczas gdy inne stany pozostaną nieobsadzone. Taka sytuacja jest możliwa np. gdy pasmo jest częściowo zapełnione, gdyż wtedy wiele stanów nieobsadzonych ma energię bardzo nieznacznie przewyższającą energię niektórych stanów zajętych i wystarczy przyłożyć do kryształu napięcie, aby niektóre elektrony uległy wzbudzeniu i zaczęły się poruszać w wybranym kierunku. Kryształ, w którym najwyższe pasmo energetyczne jest częściowo wypełnione, jest więc dobrym przewodnikiem w każdej temperaturze. Takie kryształy zaliczamy do metali.

Jeśli ostatnie obsadzone pasmo energetyczne (pasmo walencyjne) jest całkowicie wypełnione, a następne pasmo (pasmo przewodnictwa) - całkowicie wolne, to kluczową rolę odgrywa szerokość przerwy wzbronionej oddzielającej te pasma od siebie. Kryształy, w których ta szerokość przekracza 2-3 eV, są izolatorami, gdyż elektrony nie mogąc uzyskać tak dużej energii pozostają w paśmie walencyjnym i zgodnie z mechanizmem opisanym wyżej przewodnictwo nie występuje. W półprzewodnikach przerwa ta jest węższa - poniżej ok. 1 eV, co można porównać np. ze średnią energią ruchów cieplnych w temperaturze pokojowej, równą 0,025 eV. Część elektronów osiąga jednak energie większe od średniej - np. 10-krotnie większą energię (0,25 eV) osiąga jeden na 22 tysiące (zob. tekst w ramce, e^-10 = 1/22026), co często może być uważane za znaczący ułamek. Jeśli energia elektronu okaże się większa od przerwy wzbronionej, to może on przejść do pasma przewodnictwa i zająć dowolnie wybrany stan tego pasma, wnosząc wkład do przewodnictwa materiału. Im wyższa jest temperatura, tym większa jest liczba tych elektronów (znów por. tekst w ramce) - można zatem z półprzewodników wytwarzać czujniki (termistory) reagujące zmianą oporu na zmiany temperatury. Dość podobna jest zasada działania fotooporników, służących do pomiaru natężenia światła: jeśli energia światła (lub np. promieniowania nadfioletowego) jest przekazywana w „porcjach” (kwantach) przekraczających szerokość przerwy wzbronionej, to pochłanianie kwantów promieniowania spowoduje wzbudzenie elektronów z pasma walencyjnego do pasma przewodnictwa i spadek oporu.

Po elektronach, które uległy wzbudzeniu do pasma przewodnictwa, pozostaje w paśmie walencyjnym niezapełnione miejsce - „dziura”, którą można traktować jako swego rodzaju cząstkę o ładunku przeciwnym do elektronu - czyli dodatnim. Może ona zająć dowolne miejsce w paśmie walencyjnym (np. odpowiadające ruchowi w wybranym kierunku) i w ten sposób dziury wnoszą swój wkład do przewodnictwa. W półprzewodnikach samoistnych (nie zawierających domieszek) udział przewodnictwa elektronowego i dziurowego jest zbliżony, ale sytuacja ta bardzo się zmienia pod wpływem domieszek, zwłaszcza gdy ich atomy zawierają inną od pierwiastka podstawowego liczbę elektronów na ostatniej powłoce (należą do innej grupy układu okresowego). Dla krzemu (IV grupa) przykładem takiej domieszki może być fosfor (V grupa), nazywany w tych okolicznościach donorem (dawcą). Dodatkowy elektron dostarczony przez atom fosforu po dostarczeniu niewielkiej energii (rzędu 0,05 eV) przechodzi do pasma przewodnictwa, a domieszkowany fosforem krzem nazywamy ze względu na ujemny znak nośników ładunku półprzewodnikiem typu n. W analogiczny sposób atom glinu (III grupa) pełni rolę akceptora („odbiorcy”), gdyż brak jednego elektronu powoduje powstanie dziury w paśmie walencyjnym, a domieszkowany nim krzem jest półprzewodnikiem typu p. Wielki wpływ domieszek (nawet niewielkiej ich liczby) na właściwości półprzewodników jest przyczyną wysokich wymagań co do czystości stosowanych materiałów (przy produkcji „kości” komputerowych - nawet rzędu 10^-10, tzn. 1 atom na 10 miliardów).

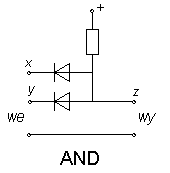
Dwie warstwy półprzewodnika przeciwnie domieszkowanego tworzą diodę warstwową (albo złączową), oznaczaną symbolem p n albo . Prąd może płynąć przez diodę tylko ze zwrotem w prawo - od obszaru p do obszaru n. Przeciwny zwrot prądu musiałby bowiem wynikać albo z ruchu ładunków dodatnich z prawa na lewo, albo z ruchu ładunków ujemnych z lewa na prawo. Jest to jednak niemożliwe, gdyż po lewej nie ma swobodnych ładunków ujemnych, ani po prawej - dodatnich. Diody znajdują zastosowanie w prostownikach, przetwarzających prąd zmienny w stały (np. zasilacze sieciowe do odbiorników telewizyjnych, komputerów...), a także w procesie demodulacji sygnałów. Powszechnie znaną odmianą diody półprzewodnikowej jest dioda elektroluminescencyjna (angielski skrót LED, potocznie „dioda świecąca”). Jej działanie opiera się na tym, że przy przepływie prądu przez diodę w kierunku przewodzenia elektrony są wprowadzane do obszaru p, gdzie szybko ulegają rekombinacji z liczniejszymi w tym obszarze dziurami, tzn. elektron spada do pasma walencyjnego „wypełniając” dziurę; podobnie dziury wprowadzone do obszaru n ulegają rekombinacji z elektronami. W czasie rekombinacji energia elektronu się zmniejsza, czyli powstała nadwyżka może być przekształcona w energię wyemitowanego kwantu światła. Odnotujmy jeszcze, że w złączu p-n może zachodzić także przeciwna przemiana energii, tzn. pochłonięty kwant światła może wytworzyć parę elektron-dziura, które na granicy obszarów p i n ulegną rozdzieleniu i mogą spowodować przepływ prądu w zewnętrznym obwodzie dołączonym do złącza. W ten sposób złącze pełni funkcję źródła prądu, czyli fotoogniwa.

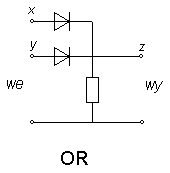
Z diod możemy zbudować obwody spełniające funkcje logiczne, tzw. bramki. Na rysunkach powyżej przedstawione są dwa takie obwody, przedstawiające bramki OR i AND. Wejścia tych bramek oznaczone zostały symbolami x i y, wyjście - symbolem z, a wartość 0 lub 1 oznacza wysoki lub niski potencjał względem ziemi (dolnego przewodu). (Należy przeanalizować działanie bramek i sprawdzić jego zgodność z tabelkami.) Łatwo wyobrazić sobie zastosowania bramek - np. alarm włącza się wtedy, gdy przerwany zostaje obwód okna 1 LUB (OR) obwód okna 2. Wadą układów diodowych jest brak wzmocnienia, czyli prąd czerpany z wyjścia może zakłócać działanie obwodów wejściowych (wejście i wyjście mogą się zamieniać rolami), a także np. dwa obwody sterowane przez jedną bramkę mogą wzajemnie zakłócać swoje funkcje.

WZMACNIANIE SYGNAŁÓW ELEKTRYCZNYCH

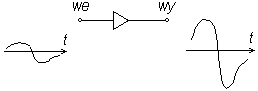
Ogólny symbol wzmacniacza i schemat jego działania widzimy na rysunku obok. Ważną cechą dobrego wzmacniacza jest możliwie dokładna proporcjonalność sygnału wyjściowego (którego przebieg czasowy przedstawiono po prawej stronie) do wejściowego (po lewej), czyli brak zniekształceń. Cecha ta nazywa się liniowością. Oczywiście, podany schemat jest skrajnie uproszczony, pominięte zostało np. zasilanie (skoro sygnał wyjściowy niesie większą energię, to konieczne jest jej dostarczenie) i szczegóły zależne od zasady działania i typu wzmacniacza. Zanim omówimy wzmacniacze stosowane we współczesnej elektronice, dokonajmy krótkiego przeglądu historycznego.

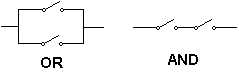
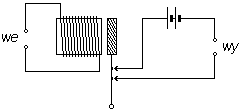
Pierwszym urządzeniem wzmacniającym impulsy elektryczne był przekaźnik elektromechaniczny, stosowany na liniach telegraficznych od ok. połowy XIX wieku. Przepływ prądu przez cewkę (zwojnicę) powoduje w przekaźniku przyciągnięcie żelaznej kotwiczki do rdzenia cewki, a w rezultacie zamknięcie lub otwarcie wtórnego obwodu elektrycznego, w którym może płynąć prąd większy od prądu sterującego przekaźnikiem. Przekaźnik jest wzmacniaczem binarnym (może znajdować się tylko w jednym z dwóch stanów), więc o wspomnianej wyżej liniowości w tym przypadku nie może być mowy. Łatwo jest zbudować z przekaźników bramki logiczne - zob. rysunek obok, gdzie zaznaczono tylko sposób zestawienia ruchomych styków (bez cewek i innych elementów). Obwód przedstawiony wyżej jest w istocie bramką NOT (inwerterem), a tabelkę dla tej bramki mamy po lewej stronie (Jeśli styki oznaczone strzałkami byłyby dołączone od lewej strony ruchomej dźwigni, mielibyśmy zamiast inwertera „powtarzacz” o trywialnej tabelce).

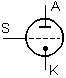
W 1906 r. Lee De Forest (USA) wynalazł triodę, próżniową lampę elektronową, która na kilkadziesiąt lat stała się podstawą konstrukcji wzmacniaczy. Katoda K w lampach elektronowych jest wykonana z metalu (lub tlenków metali), a w czasie pracy urządzenia jest podgrzewana (żarzona) wskutek przepływu prądu przez grzejnik (cienki drucik, nie zaznaczony na schemacie). Dzięki wysokiej temperaturze zachodzi zjawisko termoemisji elektronów, a jeśli anoda A ma potencjał dodatni względem katody, to wyemitowane elektrony mogą przepływać z katody do anody. Natężenie tego prądu jest sterowane potencjałem siatki S, tzn. ujemny potencjał siatki powoduje odpychanie elektronów i zmniejszenie natężenia prądu anodowego. Przy okazji wspomnijmy o diodzie próżniowej - lampie nie posiadającej siatki, a spełniającej taką samą funkcję, jak dioda półprzewodnikowa (elektrony mogą przepływać z katody do anody, lecz nie na odwrót).

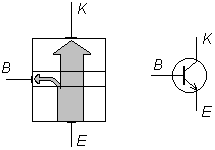
W porównaniu z lampami elektronowymi urządzenia półprzewodnikowe mają znaczną przewagę, jeśli chodzi o możliwość ich miniaturyzacji, mały pobór mocy, trwałość i odporność na wstrząsy. Wymagają też niewielkiego napięcia zasilania - kilka woltów, w porównaniu do co najmniej 100 V w lampach. Dlatego w większości zastosowań triody zostały dzisiaj wyparte przez tranzystory. Pierwszym znanym rodzajem tranzystora był bipolarny tranzystor warstwowy (albo złączowy), wynaleziony w 1948 r. przez Brattaina, Bardeena i Shockleya (USA). Składa się on z trzech warstw półprzewodnika o naprzemiennych znakach domieszek (np. n-p-n), noszących nazwy kolektor, baza i emiter. Do złącza baza-kolektor przykłada się napięcie w kierunku zaporowym (por. opisane na poprzedniej stronie działanie diody półprzewodnikowej), tak że natężenie prądu płynącego przez to złącze jest równe zeru. Stan ten ulegnie jednak zmianie, jeśli przyłożymy napięcie w kierunku przewodzenia złącza emiter-baza, gdyż wtedy do bazy są wstrzykiwane nośniki mniejszościowe (w obszarze p - elektrony), które po dotarciu do blisko położonego złącza baza-kolektor przedostają się bez przeszkód do kolektora. Ponieważ tylko niewielka część tych elektronów ulega rekombinacji w bazie, a większa część w kolektorze (obszar bazy jest cienki i stosunkowo słabo domieszkowany), więc nieduży prąd bazowy steruje w tranzystorze wielokrotnie silniejszym prądem kolektorowym.

W obwodach scalonych (np. pamięci i procesory komputerowe) występuje inny typ tranzystorów - tranzystor polowy (angielski skrót FET lub MOSFET; inaczej tranzystor unipolarny). Mamy tu dwa obszary silnie domieszkowane donorami - źródło i dren - na podłożu samoistnym lub słabo domieszkowanym akceptorami. Oddzielenie źródła od drenu sprawia, że mimo włączenia napięcia między tymi obszarami w zasadzie prąd nie powinien płynąć, gdyż na jednym ze złączy napięcie będzie miało kierunek zaporowy. Gdy jednak na trzecią elektrodę - bramkę, wykonaną z metalu i oddzieloną warstwą izolatora od powierzchni półprzewodnika - przyłożymy potencjał dodatni, pole elektryczne bramki spowoduje wciąganie elektronów ze źródła do obszaru półprzewodnika bezpośrednio sąsiadującego z bramką. W powstałym w ten sposób kanale przewodnictwa popłynie prąd między źródłem a drenem, sterowany wartością potencjału bramki.

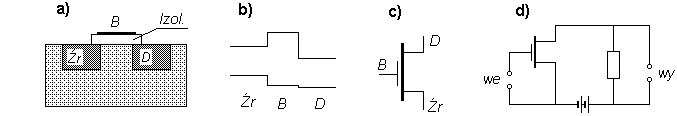
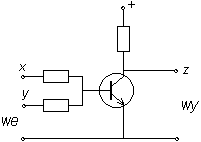
Tranzystor polowy: a) budowa, b) rozkład energii potencjalnej elektronów przy zerowym (góra) lub dodatnim (dół) potencjale bramki, c) symbol, d) schemat wzmacniacza.

Nie wyczerpaliśmy bynajmniej wszystkich zasad fizycznych, które mogłyby być wykorzystane do konstrukcji urządzeń wzmacniających sygnały różnego rodzaju. W Encyklopedii Fizyki z 1974 r. wymienione są wzmacniacze: dielektryczny, elektromaszynowy, magnetyczny, oporowy - prawdopodobnie są to rozwiązania dzisiaj już przestarzałe (?). Nowszym pomysłem jest wzmacniacz optyczny, którego zastosowanie umożliwia podtrzymywanie sygnału biegnącego światłowodem bez kłopotliwego przekształcania go w sygnał elektryczny, wzmacniania w tej postaci i ponownego przekształcania w optyczny. W ostatnich latach dużo pisze się o nieprzekraczalnych granicach miniaturyzacji obwodów scalonych, wynikających z praw rządzącej mikroświatem fizyki kwantowej (chodzi tu zwłaszcza o tzw. „tunelowanie” - przeskakiwanie elektronów między sąsiadującymi ze sobą ścieżkami przewodnictwa, jeśli rozdzielająca je warstwa izolatora jest zbyt cienka). Dalszy rozwój elektroniki miałby być w tej sytuacji oparty np. na wykorzystaniu falowych cech elektronu („komputery kwantowe”). Jest to jednak dość odległą perspektywą, a podstawowym urządzeniem elektroniki pozostaje wciąż tranzystor.

Z tranzystorów możemy zbudować bramki logiczne pozbawione wad wspomnianych wcześniej w odniesieniu do bramek diodowych. Przedstawiony obok obwód pełni funkcję bramki NOR (nie-OR), a zasadniczym jego elementem jest tranzystor warstwowy n-p-n. Jeśli w tej bramce wykorzystamy tylko jedno z wejść x i y, otrzymujemy bramkę NOT. W celu analizy działania bardziej skomplikowanych układów logicznych warto zestawić stosowane w elektronice symbole bramek:

NOT OR AND NOR NAND

ĆWICZENIE: Napisać tabelkę zależności wartości wyjściowej z od wejściowych x i y dla poniższych układów bramek:

Jednym z najważniejszych układów elektronicznych jest przerzutnik dwustabilny, który można zbudować np. z dwóch bramek NOR (rys. obok). Aby zbadać jego działanie, załóżmy że np. na wyjściu lewej bramki mamy 0. Wtedy na wyjściu prawej otrzymamy 1 - zob. tabelka bramki NOR powyżej. Ponieważ ten wysoki potencjał jest przekazywany z powrotem na dolne wejście lewej bramki, więc w analogiczny sposób przekonujemy się, że na jej wyjściu jest 0 - tak, jak założyliśmy na początku. Obie bramki „podtrzymują się” zatem wzajemnie, a wartości potencjału nie będą się zmieniać. Gdy jednak na drugie wejście prawej bramki (gdzie dotąd potencjał miał wartość 0) wprowadzimy na chwilę wysoki potencjał, spowodujemy przeskok obu bramek do przeciwnego stanu, który również będzie samoczynnie podtrzymywany dowolnie długo. Układ ten „pamięta” swój stan, który jest jednym z dwóch możliwych - taka elementarna ilość informacji nosi nazwę 1 bit. Pamięć komputerów (dokładniej - pamięć RAM, która działa po włączeniu zasilania) konstruuje się właśnie z ogromnej liczby przerzutników.

ĆWICZENIE. Zaprojektować przerzutnik zbudowany z dwóch przekaźników elektromechanicznych.

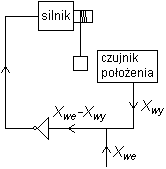
W działaniu przerzutnika widzimy sprzężenie zwrotne, polegające na przekazywaniu sygnału z wyjścia wzmacniacza z powrotem na wejście (ang. feedback). Pojęcie to ma bardzo szeroki zakres stosowalności, nie ograniczony bynajmniej do elektroniki. W omawianym wyżej przykładzie sprzężenie zwrotne jest dodatnie („skutek wzmacnia przyczynę”), ale może także być ujemne („skutek osłabia przyczynę”). Ujemne sprzężenie zwrotne jest podstawą wszelkich układów automatycznej regulacji i sterowania, czego przykładem jest przedstawiony obok schemat sterowania położeniem ciężaru wiszącego na linie. Sygnał sterujący został na nim oznaczony jako X_we; jak widzimy, następuje porównanie go (odjęcie) z sygnałem X_wy pochodzącym od czujnika położenia ciężaru. Sygnał różnicowy X_we-X_wy po wzmocnieniu zasila silnik podnoszący lub opuszczający ciężar, przy czym zwrot jego przesunięcia jest dobrany tak, aby wartość X_we-X_wy uległa zmniejszeniu. Licznych przykładów dodatniego i ujemnego sprzężenia zwrotnego dostarcza obserwacja zjawisk ekonomicznych i społecznych, np.:

- spirala inflacyjna: wzrost cen powoduje żądania wzrostu płac i strajki, wzrost płac z kolei podwyższa koszty produkcji i zmusza producentów do podwyżek cen swoich towarów (dodatnie sprzężenie zwrotne),

- rynkowy mechanizm stabilizacji cen: gdy cena towaru wzrasta, produkcja staje się bardziej opłacalna, co skłania przedsiębiorców do inwestycji dających jej wzrost, do odpowiedniej zmiany profilu produkcji lub do importu. Zwiększona podaż jest czynnikiem hamującym wzrost cen (ujemne sprzężenie zwrotne).

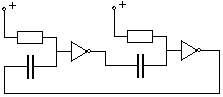
Aby ujemne sprzężenie zwrotne dobrze spełniało zadanie automatycznej regulacji skali zjawiska, powinno działać bez opóźnienia. W przeciwnym wypadku może nastąpić wzbudzenie drgań (oscylacji). W dziedzinie ekonomii przykładem tego zjawiska w Polsce jest (był?) tzw. cykl świński - następujące co kilka lat wahania produkcji wieprzowiny i cen mięsa (po 1989 roku) lub jego dostępności na rynku (w okresie wcześniejszym). Niższa podaż mięsa pociąga za sobą wzrost ceny lub reakcję władz (w formie podwyżki cen skupu, kredytów na zakup paszy itd.), co zachęca rolników do zwiększenia hodowli; jednak na efekty tych decyzji przychodzą dopiero po upływie kilkunastu miesięcy, kiedy ceny spadają, a to z kolei skłania hodowców lub władze do decyzji odwrotnych. Prostym przykładem elektromechanicznym tego samego zjawiska jest działanie przerywacza dzwonkowego na prąd stały: przepływ prądu przez cewkę powoduje przyciągnęcie kotwiczki i przerwanie obwodu, a po ustaniu przepływu prądu kotwiczka powraca, z opóźnieniem wywołanym przez jej bezwładność (Taki przerywacz wywołuje duże zakłócenia odbioru fal elektromagnetycznych, dlatego domowe dzwonki działają na innej zasadzie). W elektronice analogiczny układ określa się jako astabilny, a przykładem jest multiwibrator astabilny na schemacie z lewej strony. Obok elementów wprowadzonych już wcześniej widzimy tu kondensatory, których funkcja polega na gromadzeniu ładunku elektrycznego (dodatniego na jednej z okładek kondensatora, a ujemnego na drugiej). Aby zrozumieć działanie multiwibratora załóżmy, że na wejściu lewej bramki NOT mamy potencjał 1, na jej wyjściu 0, a prawy kondensator jest nienaładowany. Dla nienaładowanego kondensatora nie ma różnicy potencjałów między jego okładkami, zatem na wejściu prawej bramki mamy 0, czyli na jej wyjściu 1, a ponieważ ten wysoki potencjał wraca na wejście pierwszej bramki, więc stwierdzamy zgodność z początkowym założeniem (jak w przerzutniku). Stan ten będzie się jednak utrzymywał tylko przez pewien czas, gdyż wejście prawej bramki jest także podłączone przez opornik do wysokiego potencjału. Prąd płynący przez opornik będzie stopniowo ładował ten kondensator, co oznacza wzrost potencjału jego prawej okładki (tzn. wejścia bramki). W pewnym momencie prawa bramka przeskoczy do przeciwnego stanu, co pociągnie za sobą zmianę stanu lewej, a ten odwrócony stan utrzyma się tak długo, dopóki lewy kondensator pozostanie nienaładowany itd. Częstość drgań generowanych przez multiwibrator zależy od oporu oporników i pojemności kondensatorów (zob. tekst w ramce) - zależnie od nich obwód może sterować np. miganiem lampek lub dźwiękiem wysyłanym przez głośnik. Opisana tu funkcja kondensatorów dotyczy także obwodów scalonych, gdzie rządzą one znacznie szybciej przebiegającymi przebiegami czasowymi.

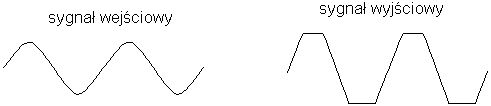
Na zakończenie tego rozdziału powróćmy jeszcze do pojęcia liniowości, wspomnianego wcześniej w odniesieniu do wzmacniaczy. Ujmując to zagadnienie ogólniej powiemy, że liniowość polega na „proporcjonalności skutku do przyczyny”, co można zilustrować przykładami i kontrprzykładami z najróżniejszych dziedzin nauki. Bramki logiczne są, oczywiście, układami nieliniowymi, gdyż słaby impuls nie powoduje w ogóle zmiany ich stanu, a po przekroczeniu progu czułości przeskok również nie zależy od wielkości impulsu (por. uwagi o przekaźniku na s.3). Realne wzmacniacze (np. akustyczne) są zwykle liniowe w pewnych granicach, po przekroczeniu których pojawiają się efekty nieliniowe, np. dla sygnałów o dużej amplitudzie - obcinanie ich maksimów (tzw. przesterowanie, zob. rys.). Prawa fizyki mają często charakter liniowy, np. prawo Ohma oznacza proporcjonalność natężenia prądu (skutku) do napięcia (przyczyny), podobną zależność Q od U mamy dla kondensatorów - warto jednak zauważyć, że realne oporniki i kondensatory wykazują czasem pewne odstępstwa od liniowości. Dioda jest elementem zdecydowanie nieliniowym, gdyż odwrócenie znaku napięcia nie spowoduje odwrócenia kierunku prądu - jeśli napięcie zmieni kierunek z przewodzącego na zaporowy, prąd spadnie do zera! Nakładanie się dwóch fal dźwiękowych lub świetlnych można uznać za zjawisko liniowe, gdyż w większości ośrodków obowiązuje zasada superpozycji (składania) fal, według której jedna z nich nie wpływa na bieg drugiej. Suma przyczyn (wzbudzenie jednej i drugiej fali) powoduje zatem sumę skutków. Nie jest to jednak prawdą dla wysokich fal wodnych, gdyż podwojenie wysokości może pociągnąć za sobą załamanie wysokiego grzbietu fali, a więc efekt jakościowo odmienny!

Sięgnijmy jeszcze do przykładów spoza fizyki czy techniki. Katastrofa w Czarnobylu naraziła stosunkowo niewielką grupę ludzi na duże dawki promieniowania (których szkodliwe skutki są dobrze znane) oraz znacznie większą liczbę ludności na dawki małe, których następstwa są trudne do ustalenia. Oceniając skutki katastrofy przyjęto hipotezę liniową, według której dana dawka promieniowania powoduje stałą liczbę przypadków raka niezależnie od tego, czy ta dawka rozkłada się na większą, czy mniejszą liczbę osób - inaczej mówiąc, prawdopodobieństwo zachorowania jest ściśle proporcjonalne do wielkości dawki, zarówno dla dawek dużych, jak i bardzo małych. Ostatnio ta hipoteza jest poważnie kwestionowana - bardzo możliwe, że niewielkie uszkodzenia tkanek łatwo ulegają naprawie, tak że małe dawki przestają być szkodliwe (a nawet mogą mieć korzystny wpływ na zdrowie!). Zjawiska społeczne i ekonomiczne są na ogół tak skomplikowane, że zależności liniowe (np. między ceną a popytem) można rozpatrywać tylko jako pierwsze, najgrubsze przybliżenie.

ĆWICZENIE. Podatkiem liniowym nazywa się podatek o stałej skali, niezależnej od wysokości dochodów. Czy w razie jego obowiązywania wspólne opodatkowanie małżonków może przynieść podatnikom korzyści?

ĆWICZENIE. Ocenić orientacyjnie minimalną liczbę bitów, niezbędną do: a) wyboru jednej osoby spośród mieszkańców Polski, b) ustalenia terminu i miejsca spotkania z kolegą, c) przesłania podpisu (rysunku) z dokładnością umożliwiającą jego weryfikację, d) przesłania strony książki (tylko tekst, bez danych graficznych).

TECHNIKA ANALOGOWA A TECHNIKA CYFROWA

Sygnał elektryczny otrzymywany z mikrofonu jest sygnałem analogowym, czyli przybierającym dowolną wartość, zależnie od natężenia dźwięku. Pomiar tej wielkości (w celu wzmocnienia lub zapisu) jest obarczony, oczywiście, większym lub mniejszym błędem wynikającym z dokładności urządzeń. Jeśli sygnał taki będzie wielokrotnie zapisywany, kopiowany i odtwarzany, to błędy będą się kumulowały - będziemy słyszeli coraz więcej szumów. Sygnał cyfrowy jest to ciąg zer i jedynek, który można odczytywać i zapisywać bez błędu, jeśli tylko na żadnym etapie zakłócenia nie staną się tak duże, że uniemożliwią odróżnienie zera od jedynki. Aby poglądowo zilustrować różnicę między jedną a drugą techniką, porównajmy obliczenia wykonywane na suwaku logarytmicznym („technika analogowa”) z rachunkami na liczydle („technika cyfrowa”). Na suwaku wykonujemy obliczenia z dokładnością 2-3 cyfr wartościowych, nieco dokładniej przy bardzo starannym ustawieniu suwaka, a nieco mniej dokładnie dla długiego ciągu działań. Na liczydle wykonujemy obliczenia dokładne (wyłączając pomyłki). Ale proste działanie na suwaku wymaga często długich i skomplikowanych operacji na liczydle.

Techniką analogową posługuje się radio, część stacji telewizyjnych, „zwykła” telefonia i niektóre sieci telefonii komórkowej. W technice cyfrowej działają komputery i sieci komputerowe, odtwarzacze kompaktowe i nowoczesne systemy łączności. Aby przekazać lub zapisać w technice cyfrowej np. dźwięk (ogólniej - dowolny sygnał, który „na początku” był analogowy), niezbędne jest użycie przetwornika analogowo-cyfrowego. Odwrotny przetwornik cyfrowo-analogowy jest niezbędny przy odtworzeniu dźwięku, gdyż głośnik wymaga sygnału analogowego (również sygnał sterujący jasnością danego punktu ekranu w kineskopach telewizyjnych jest analogowy). W przetwarzaniu sygnału z postaci analogowej w cyfrową można wyróżnić następujące etapy:

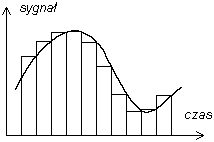
a) kwantyzacja - zaokrąglenie wyniku pomiaru do całkowitej wielokrotności pewnej zadanej jednostki (np. zaokrąglenie 8,12 do 8,10, a 8,13 do 8,15). Oczywiście, kwantyzacja jest źródłem pewnego błędu, ale błąd ten jest kontrolowany, w razie potrzeby można go zmniejszyć, a przede wszystkim nie ulega dalej zwiększeniu przy przesyłaniu i przekształcaniu sygnału,

b) kodowanie - wyrażenie otrzymanej liczby w układzie dwójkowym,

c) dla sygnałów zależnych od czasu (np. sygnału akustycznego) - próbkowanie (ang. sampling), czyli odpowiednio częste powtarzanie pomiaru. Dla przykładu, dźwięk na płytach kompaktowych jest próbkowany z częstotliwością 44 kHz (44 tysiące razy na sekundę), a każdorazowy pomiar ma dokładność 16 bitów, co oznacza 2¹⁶ = 65536 poziomów kwantyzacji. Telefonia komórkowa (GSM) stosuje próbkowanie z częstotliwością 8 kHz i dokładnością 8 bitów.

Szeroko znane są zalety techniki cyfrowej. Po pierwsze, przekaz sygnału jest odporny na szumy i zakłócenia, o ile nie przekroczą one pewnego założonego poziomu. W przypadku silnych zakłóceń technika cyfrowa oferuje zresztą skuteczne metody korekty błędów („bity kontrolne” dołączane do przekazu). Po drugie, przekształcanie ciągu danych cyfrowych jest łatwe i może spełniać bardzo wyrafinowane funkcje, m.in.:

a) szyfrowanie,

b) multipleksowanie - łączenie kilku sygnałów z różnych źródeł w jednym przekazie (np. przesyłanie kilku rozmów telefonicznych jednym kablem),

c) kompresja danych - usuwanie z przekazu „zbędnych bitów” (np. dla dźwięku - zapisanie ciszy w postaci umownego skrótu),

d) w fotografii i w filmie - bardzo szerokie możliwości przetwarzania obrazu (np. fotomontaż),

e) w radiu - możliwość wybrania przez odbiorcę serwisu informacyjnego (takie radio - DAB - działa już w Polsce, wymaga zakupu specjalnego odbiornika, niestety dość drogiego),

f) w telewizji - możliwość wprowadzenia podwyższonego standardu jakości obrazu (np. szeroki ekran z rozdzielczością 1080 linii zamiast obecnych 625); także połączenie funkcji telewizora i monitora komputerowego.

ĆWICZENIE. Dlaczego rozpowszechnienie techniki cyfrowej niepokoi producentów nagrań muzycznych?

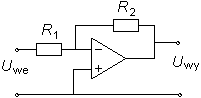
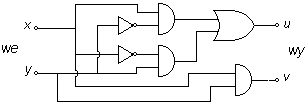
Różnicę między techniką cyfrową a techniką analogową wyraźnie widać przy porównaniu sposobu wykonywania dzia­łań matematycznych. Obok widzimy schemat sumatora dwójkowego, służącego do dodania w układzie dwójkowym dwóch liczb jednocyfro­wych x i y, w wyniku czego otrzymamy liczbę dwucyfrową o cyfrach u i v (tzn. u+2v). Łącząc takie sumatory można dodawać liczby dwucyfrowe („sumator czwórkowy”) itd. Dodawanie sygnałów analogowych mogłoby w zasadzie polegać na zestawieniu dwóch źródeł szeregowo (dodawanie napięć) lub równolegle (dodawanie natężeń prądu) - jednak brak wzmocnienia powodowałby wady wspomniane wcześniej w związku z bramkami diodowymi. Najczęściej wykonuje się działania matematyczne na sygnałach analogowych przy użyciu wzmacniacza operacyjnego - wzmacniacza o bardzo dużym współczynniku wzmocnienia napięciowego i pobierającego bardzo niewielki prąd, przeznaczonego do pracy w układzie z ujemnym sprzężeniem zwrotnym. Wzmacniacz operacyjny ma zwykle dwa wejścia oznaczane na schemacie symbolami + i -, a jeśli odpowiednie napięcia wejściowe oznaczymy symbolami U₊ i U_-­ , to napięcie wyjściowe równa się różnicy U₊-U_-­ pomnożonej przez bardzo duży współczynnik. Takie wzmacniacze produkuje się jako obwody scalone składające się z ok. 30 tranzystorów. Najprostsze wykorzystanie właściwości wzmacniacza operacyjnego widzimy na schemacie obok. Dolny przewód podłączony do wejścia + jest „masą” - poziomem zerowym, względem którego liczy się wszystkie napięcia. Analizując działanie obwodu można by sądzić, że ze względu na bardzo silne wzmocnienie otrzymujemy na wyjściu wielką wartość U_wy; jednak gdyby tak było, to przez opornik R₂ popłynąłby bardzo duży prąd w lewo podnosząc wartość U_- , co z kolei - dzięki wzmocnieniu - silnie obniżyłoby napięcie wyjściowe (zasada ujemnego sprzężenia zwrotnego). Należy więc wyciągnąć wniosek, że U_wy jest „rozsądnie nieduże”, a U_- - bardzo bliskie zera. Dalej zauważmy, że skoro wzmacniacz nie pobiera prądu, to przez oba oporniki płynie ten sam prąd I. Napięcie wejściowe jest zatem równe U_we = IR₁, wyjściowe - U_wy = -IR₂, czyli

Wzmocnienie uzyskiwane w tym obwodzie zależy więc od oporności R₁ i R₂, ale nie od parametrów samego wzmacniacza.

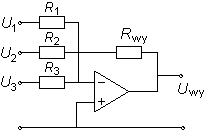
Niewielka modyfikacja przedstawionego wyżej obwodu pozwoli zrealizować zadanie dodania sygnałów analogowych, np. U₁, U₂ i U₃ na schemacie obok. Widzimy, że natężenie prądu płynącego przez opornik R_wy jest równe sumie natężeń prądów przez R₁, R₂ i R₃, a stąd

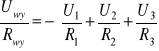
W szczególnym przypadku, gdy R₁ = R₂ = R₃ = R_wy, otrzymujemy U_wy = -(U₁ + U₂ + U₃). Włączenie do obwodu kondensatora pozwala zrealizować bardziej skomplikowane operacje matematyczne, np. całkowanie lub różniczkowanie.

Wadą obliczeń analogowych jest ich niedokładność (błąd rzędu 1%), co wyklucza ich użycie np. w bankowości. W pewnych okolicznościach nie musi to być jednak istotną przeszkodą - np. w niektórych obliczeniach inżynierskich lub w prognozowaniu pogody występują bardzo długie i skomplikowane obliczenia opierające się na niezupełnie dokładnych danych, a wyniki także wystarczą przybliżone. Fakt, że całe obliczenie jest wykonywane „na jednym wzmacniaczu”, może być zaletą - mniej trzeba tranzystorów i urządzenie może działać szybciej. Do lat 70-tych komputery analogowe lub hybrydowe (łączące obwody cyfrowe i analogowe) w pewnych specjalistycznych zastosowaniach wygrywały z cyfrowymi. Techniki cyfrowe są jednak bardziej uniwersalne, zmiana metody obliczeniowej oznacza w nich tylko zmianę programu, natomiast w obliczeniach analogowych trzeba „zbudować komputer od początku”. W prostych urządzeniach automatycznych („gdy jest zimno, włączyć ogrzewanie... gdy bardzo zimno, ogrzewać na maksimum...”) wzmacniacze operacyjne zachowały wciąż mocną pozycję.

TECHNOLOGIA PRODUKCJI OBWODÓW SCALONYCH

Miniaturyzacja obwodów scalonych pozwala zwiększać liczbę elementów (np. tranzystorów) w jednej kości (ang. chip), dzięki czemu procesory mogą wykonywać bardziej skomplikowane funkcje, a pamięć jest pojemniejsza. Zwiększa się także szybkość działania urządzeń, bo prędkość rozchodzenia się impulsów elektrycznych jest skończona - równa prędkości światła. Obecna technologia sięga ok. 20 milionów tranzystorów i innych elementów w jednej kości, szybkość działania jest rzędu miliarda elementarnych operacji na sekundę (taktowanie mikroprocesorów zegarem 1 GHz), a rozmiary najmniejszych struktur wynoszą ok. 0,14 m.

Działające w dzisiejszych komputerach kości są układami scalonymi opartymi na krzemie. Obok wysokiej czystości (jak już wcześniej wspomniano, rzędu 10^-10) wymagana jest doskonale regularna struktura krystaliczna krzemu, jaka występuje w monokrysztale - pojedynczym dużym krysz­tale, w przeciwieństwie do struktury polikrystalicznej, w której pozlepiane drobne kryształki mają przypadkowe kierunki osi. Pionierem technologii produkcji monokryształów był w latach 20-tych i 30-tych XX wieku polski inżynier Czochralski - jego metoda polega na bardzo powolnej krystalizacji ciekłego krzemu, a powstający monokryształ ma kształt pręta, który w miarę narastania jest wyciągany z cieczy w górę. Taki pręt ma (wg dzisiejszej techniki) ok. pół metra długości i średnicę 20 cm, a do produkcji obwodów scalonych tnie się go na plasterki grubości 20 m. Poszczególne elementy obwodu (obszary domieszkowane, ścieżki, elektrody) są wytwarzane na takim plasterku dzięki technice noszącej nazwę fotolitografii. Polega ona na przenoszeniu odpowiedniego wzoru z maski (gdzie obraz jest 4-5 krotnie powiększony) na powierzchnię płytki krzemowej za pośrednictwem układu optycznego, działającego w zakresie nadfioletu (długość fali od 0,193 m do 0,365 m). Powierzchnię płytki pokrywa się uprzednio warstwą polimeru fotoczułego, a po naświetleniu przemywa chemikaliami, które zmywają to, co zostało naświetlone (albo co zostało nienaświetlone). W kolejnej fazie inne chemikalia powodują trawienie nieosłoniętych elementów powierzchni i np. wprowadzanie domieszek... Cały proces powtarza się ok. 20 razy z różnymi maskami - tak powstają kolejne warstwy obwodu. Wielkie wymagania co do precyzji naniesienia poszczególnych elementów sprawiają, że urządzenia są niesłychanie kosztowne, a produkcja jest opłacalna tylko w masowej skali.

Wielkość wytworzonych tą metodą elementów jest ograniczona od dołu przez efekty dyfrakcji (inaczej ugięcia, zob. wstawka na s. 16), czyli nie-prostoliniowego rozchodzenia się światła, co pociąga za sobą rozmycie obrazu. Prawa optyki narzucają tu warunek, że rozdzielczość obrazu (wielkość rozróżnialnych elementów) nie może być mniejsza od długości fali światła. Dlatego miniaturyzacja obwodów scalonych szła dotąd w parze ze zmniejszaniem długości fali promieniowania stosowanego przy ich produkcji. Dalej jednak taka ewolucja może napotkać na barierę polegającą na tym, że dla dalekiego nadfioletu i dla promieni Röntgena (których długość fali jest jeszcze mniejsza) nie istnieją dobre soczewki. Inna bariera polega na tunelowaniu - przeskakiwaniu elektronów między sąsiadującymi ze sobą ścieżkami przewodnictwa, jeśli rozdzielająca je warstwa izolatora jest zbyt cienka. Z tego powodu wielkość elementów tranzystora MOS nigdy nie zejdzie poniżej ok. 0,03 m. Technologie przyszłości mogłyby w tej sytuacji polegać na:

a) wykorzystaniu zwierciadeł (układów odbijających) zamiast soczewek (ale dla promieni Röntgena dobre zwierciadła także niełatwo wyprodukować),

b) zastosowaniu litografii elektronowej zamiast optycznej, tzn. tworzeniu obrazu za pośrednictwem wiązki elektronów (ale jak dotąd, wiązki elektronów działają zbyt wolno, gdyż rysują kolejno jedną linię po drugiej, zamiast jednym błyskiem),

c) zamiast trawienia - osadzaniu warstw atomowych poprzez kierowanie na płytkę wiązek atomów lub cząsteczek,

d) zmianie półprzewodnika - już dzisiaj stosuje się czasem kości z arsenku galu GaAs zamiast krzemu (są szybciej działające, ale droższe),

e) zastąpieniu tranzystorów wzmacniaczami optycznymi (sygnałem jest wiązka światła, a nie prąd),

f) w dalszej przyszłości - oparciu zasady działania komputera na prawach fizyki kwantowej („komputer kwantowy”?).

PODSTAWY TELEKOMUNIKACJI

Około 1840 r. wynaleziono telegraf elektromagnetyczny, a wkrótce potem alfabet Morse'a. Pierwszy kabel transatlantycki położono w roku 1858. Miał on jednak bardzo małą przepustowość - mniejszą od 1 bita na sekundę (oczywiście, wtedy bit jako jednostka ilości informacji nie był stosowany). Przyczyną tego był znaczny opór tak długiego przewodu (ok. 10 kΩ) w połączeniu z jego dużą pojemnością elektryczną (ok. 20 F). Jak wynika z teorii przedstawionej we wstawce na stronie 6, stała czasowa takiego obwodu wynosi ok. 0,2 s, co oznacza, że narastanie sygnału, a potem jego spadek do zera w sumie zajmują czas rzędu sekundy. Przesyłanie impulsów w szybszym tempie oznaczałoby stratę informacji zarówno wskutek ich tłumienia (słabnięcia), a także wskutek dyspersji - „rozmywania się”. Różnicę między tymi dwoma zjawiskami ilustruje poniższy rysunek.

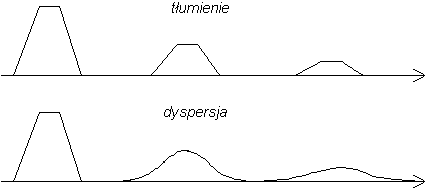
W 1876 r. wynaleziony został telefon (A.G.Bell, USA). Przekaz dźwięku za pośrednictwem sygnałów elektrycznych wymaga, oczywiście, ograniczenia wspomnianych powyżej niepożądanych efektów. Pierwsza rozmowa telefoniczna poprzez kabel położony na dnie Atlantyku miała miejsce w 1956 r., a zrealizowano ją instalując na kablu co pewien odcinek wzmacniacze pośrednie - tzw. repetory („powtarzacze”). W przypadku omawianego kabla było ich 51, co ok. 60 km, a ich zadaniem jest kształtowanie od nowa sygnałów, zanim zdążą ostatecznie zaniknąć. Ta zasada postępowania obowiązuje także i dzisiaj, np. w telekomunikacji światłowodowej.

ĆWICZENIE. Ile razy zwiększy się szybkość transmisji kabla o danej długości, jeśli podwoimy ilość repetorów, czyli dwukrotnie skrócimy odległość między nimi? (Wskazówka: zob. informacje na temat stałej czasowej obwodu RC we wstawce na s. 6).

a

- - 9 -

Skala wielkości w mikroświecie:

1 mm

0,1 mm włos ludzki

10 m

1 m bakterie

0,1 m wirusy

10 nm cząsteczka DNA

1 nm atomy

0,1 nm

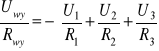
x y u v

0 0 0 0

0 1 1 0

1 0 1 0

1 1 0 1

Napięcie U (różnica potencjałów) mię­dzy okładkami kondensatora jest pro­porcjonalne do jego ładunku Q. Stałą proporcjonalności nazywamy pojemno­ścią kondensatora i oznaczamy symbo­lem C

Q = C·U

Można wykazać, że w obwodzie zawierającym opornik o oporze R i kondensator o pojemności C czas nałado­wania lub rozładowania konden­satora jest w przybliżeniu równy iloczynowi R·C. Wielkość tę nazywamy czasem charakterystycznym lub stałą czasową obwodu.

x y z

0 0 1

0 1 0

1 0 0

1 1 0

Tranzystor n-p-n. Z lewej - przepływ elektronów (grubość strzałki jest proporcjonalna do ich liczby). Z prawej - symbol.

x y

0 1

1 0

x y z

0 0 0

0 1 1

1 0 1

1 1 1

x y z

0 0 0

0 1 0

1 0 0

1 1 1

Energia promieniowania elektromagnetycznego może być przekazywana tylko w niepodzielnych porcjach nazywanych kwantami. Wartość kwantu promieniowania wyraża się wzorem E = hf, gdzie f jest częstotliwością fali, a h - stałą Plancka. Ponieważ częstotliwość jest powiązana z długością fali  i jej prędkością c wzorem f = c/, więc E = hc/, a po wprowadzeniu danych liczbowych i wyrażeniu E w elektronowoltach otrzymujemy wygodny wzór

E[eV] = 1,24/[m]

Dla światła widzialnego długość fali zawiera się w przedziale od ok. 0,4 m (fiolet) do ok. 0,75 m (czerwień), co oznacza energię kwantu od 1,7 eV (czerwień) do 3 eV (fiolet).

Według praw fizyki statystycznej prawdopodobieństwo tego, że cząstka osiągnie energię E, jest odwrotnie proporcjonalne do liczby e=2,718 do potęgi E/E_śr, gdzie E_śr jest średnią energią, proporcjonalną do temperatury w skali Kelvina.

p ≈ e^-E/Eśr

Elektronowolt (eV) jest to energia, jaką uzyskuje ładunek elementarny (np. elektron) po przejściu różnicy potencjałów 1 V. W fizyce atomowej jest to często stosowana jednostka, a jej przeliczenie na dżule ma postać 1 eV = 1,6·10^-19 J.

E

Z lewej: poziomy energetyczne elektronu w atomie (przykładowy schemat). W środku: pasma energetyczne elektronu w krysztale. Z prawej: stany elektronu swobodnego.

Opór elektryczny drutu o długości l i polu przekroju poprzecznego S wyraża się wzorem

R = ρl/S

gdzie parametr ρ zależy od materiału drutu. Nazy­wamy go opornością właściwą materiału, a jeśli R wyraża się w omach, l w metrach, a S w m², to - jak wi­dać ze wzoru - jednostką oporności właściwej jest Ω·m.

---