Sprawozdanie z labolatorium Mechaniki Ciała Sztywnego

Temat ćwiczenia : Skręcanie.

1.Czyste skręcanie pręta kołowego

Przedmiotem badanym był pręt o przekroju kołowym o średnicy d = 20 mm, oraz długości l = 100,8 mm. Na ramieniu r = 300 mm umieszczane były kolejno ciężarki od 5 do 25 kg, i mierzony był kąt skręcenia pręta w dwóch przekrojach odległych od umocowania pręta odpowiednio:

• czujnik 1 : l₁ = 223 mm

• czujnik 2 : l₂ = 833 mm

Czujniki wskazywały przemieszczenia dźwigienek o długości r₁ = r
=100 mm .

Wskazania czujników zostały zestawione w tabeli poniżej:

Obciążenie F(N)	Wskazania czujnika 1 (mm)	Wskazania czujnika 2 (mm)	Kąt skręcenia φ (rad/stopni)	Kąt skręcenia φ (rad/stopni)
49,05	0,2	0,925	0,002/0,11	0,0093/0,53
98,1	0,35	1,845	0,0035/0,2	0,0184/1,06
147,15	0,65	2,8	0,0065/0,37	0,028/1,603
196,2	0,89	3,715	0,0089/0,51	0,0371/2,127
245,25	1,12	4,665	0,0112/0,64	0,0466/2,671

Kąty skręcenia φ
i φ
obliczamy z zależności :

tg(φ
)=
, tg(φ
)=
, skąd :

φ
=arctg(
) oraz φ
= arctg(
) ,gdzie

W
-wskazanie czujnika 1

W
- wskazanie czujnika 2

Wyniki obliczeń zostały umieszczone w tabeli wyżej.

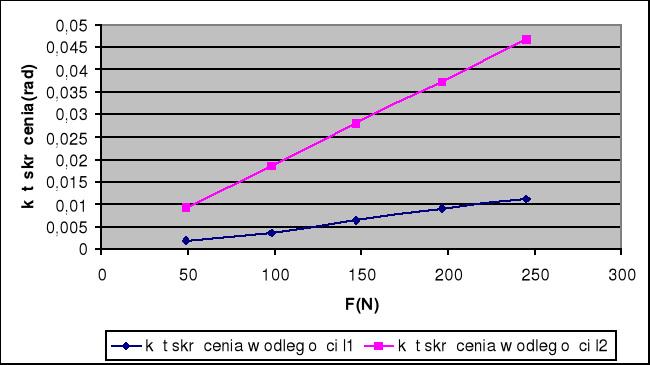
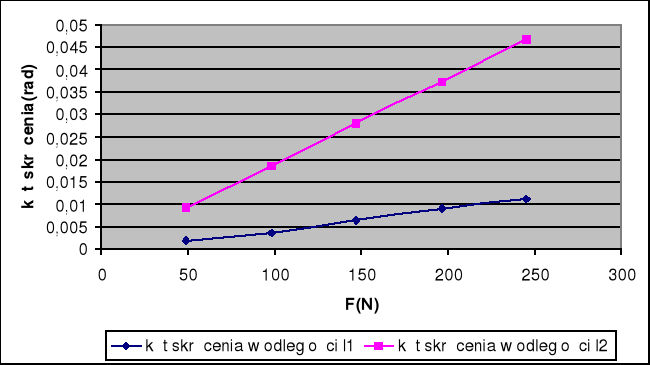
Można teraz przedstawić wykres zależności kąta skręcenia  od obciążenia F:

Oraz zależność kątów skręcenia w zależności od momentu siły:

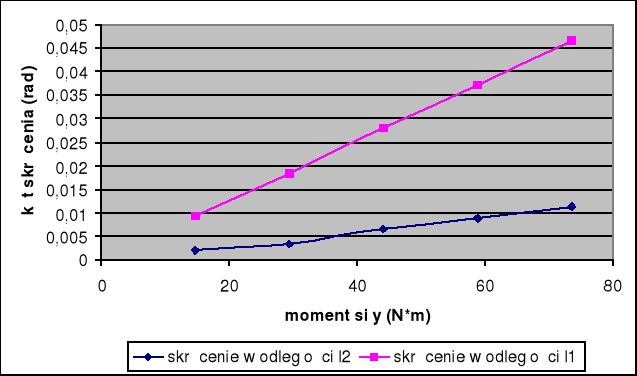
2.Czyste skręcanie pręta o przekroju kwadratowym

Doświadczenie jak w punkcie (1), lecz pręt o przekroju kwadratowym o następujących wymiarach:

a = 20 mm

l = 1008 mm

R= 300 mm

l₁ = 178 mm

l₂ = 866 mm

Znowu brane pod uwagę były tylko wskazania czujnika 1. Zestawione one zostały poniżej:

Obciążenie F(N)	Wskazania czujnika 1 (mm)	Wskazania czujnika 2 (mm)	Kąt skręcenia φ (rad/stopni)	Kąt skręcenia φ (rad/stopni)
49,05	0,155	0,715	0,002/0,09	0,00714/0,40
98,1	0,32	1,435	0,0032/0,18	0,0143/0,82
147,15	0,465	2,165	0,0047/0,27	0,022/1,24
196,2	0,62	2,895	0,0062/0,36	0,029/1,66
245,25	0,78	3,62	0,0078/0,45	0,036/2,07

Kąty φ
i φ
obliczamy z wyżej podanych zależności i wstawiamy do tabelki.

Wykres zależności kąta skręcenia od siły działającej:

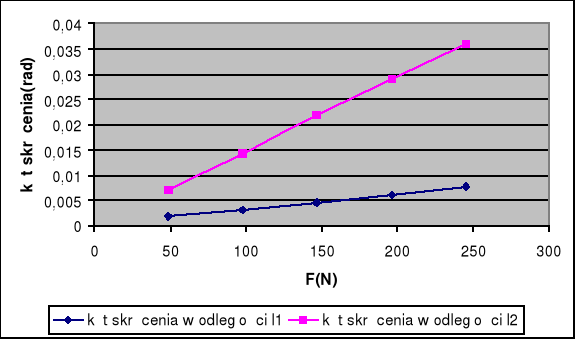
Wykres zależności kąta skręcenia od momentu siły:

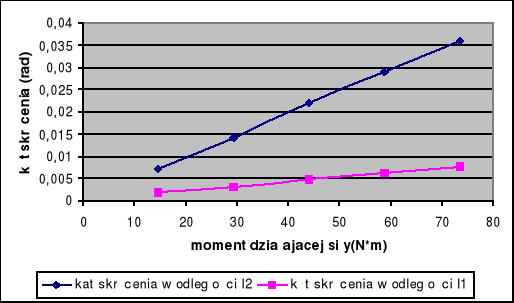
1.Wartości teoretyczne i porównanie z wynikami doświadczeń

1. Wyznaczenie modułu Kirchhoffa (dla pręta o przekroju kołowym)

Korzystając z naszych badań (punkt 1) możemy określić moduł Kirchhoffa pręta o przekroju kołowym. Należy tu wykorzystać zależność:

po przekształceniu :

J₀ = 1,57 · 10^-8 m⁴ - biegunowy moment bezwładności dla pręta o promieniu r = 10 mm

Korzystając z wartości kąta skręcenia pręta w przekrojach 1 i 2 można określić moduły Kirchhoffa dla poszczególnych pomiarów:

Obciążenie F(N)	Wskazania czujnika 1 (mm)	Wskazania czujnika 2 (mm)	Kąt skręcenia φ (rad/stopni)	Kąt skręcenia φ (rad/stopni)	Moduł Kirchoffa dla φ (10 MPa)	Moduł Kirchoffa dla φ (10 MPa)
49,05	0,2	0,925	0,002/0,11	0,0093/0,53	1,05	0,84
98,1	0,35	1,845	0,0035/0,2	0,0184/1,06	1,19	0,849
147,15	0,65	2,8	0,0065/0,37	0,028/1,603	0,965	0,837
196,2	0,89	3,715	0,0089/0,51	0,0371/2,127	0,939	0,842
245,25	1,12	4,665	0,0112/0,64	0,0466/2,671	0,933	0,838

Średnia wartość modułu Kirchoffa obliczona na podstawie pomiarów wynosi: G=0,928⋅10
MPa

Wartość tablicowa modułu Kirchoffa wynosi :G
=0,808⋅10
MPa

Obliczenie jednostkowego kąta skręcenia  dla pręta o przekroju kołowego.

Jednostkowy kąt skręcenia oblicza się z zależności:

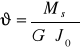
Na podstawie pomiarów jednostkowy kąt skręcenia obliczamy z zależności:

Wyniki obliczeń oraz pomiarów zostały zestawione w tabeli poniżej:

Obciążenie F(N)	Moment skręcający M (N⋅m)	Jednostkowy kąt skręcenia θ (wartość teoretyczna)	Jednostkowy kąt skręcenia θ (na podstawie pomiarów)
49,05	14,715	1,16E-02	1,01E-02
98,1	29,43	2,32E-02	1,89E-02
147,15	44,145	3,48E-02	3,14E-02
196,2	50,76	4,64E-02	4,22E-02
245,25	73,575	5,80E-02	5,31E-02

Wartości kąta skręcenia wyliczonego na podstawie pomiarów różni się od wartości kąta teoretycznego przy małym obciążeniu nieznacznie ,natomiast wraz ze wzrostem obciążenia ta różnica wzrasta.

Obliczenie jednostkowego kąta skręcenia  dla pręta o przekroju kwadratowym.

Jednostkowy kąt skręcenia oblicza się z zależności:

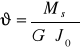
,gdzie J
=0,141⋅a
=0,141⋅(20)
=22560mm
=22560⋅10
m

G=0,928⋅10
MPa

Na podstawie pomiarów jednostkowy kąt skręcenia obliczamy z zależności:

Wyniki obliczeń oraz pomiarów zostały zestawione w tabeli poniżej:

Obciążenie F(N)	Moment skręcający M (N⋅m)	Jednostkowy kąt skręcenia θ (wartość teoretyczna)	Jednostkowy kąt skręcenia θ (na podstawie pomiarów)
49,05	14,715	0,007	0,009
98,1	29,43	0,014	0,016
147,15	44,145	0,021	0,024
196,2	50,76	0,024	0,031
245,25	73,575	0,035	0,039

Różnica miedzy jednostkowym kątem skręcenia wyliczona teoretycznie i wyliczona na podstawie pomiarów jest stała i nie zmienia się wraz ze wzrostem obciążenia.

---