SPRAWOZDANIE Z 3. LABORATORIUM Z FIZYKI I
Z DNIA 28.10.1998 PT:

„POMIAR SZEROKOŚCI SZCZELINY ORAZ NIEPRZEZROCZYSTEGO PASKA NA PODSTAWIE ZJAWISKA DYFRAKCJI ŚWIATŁA”

(22)

Podczas tego laboratorium mieliśmy za zadanie znaleźć szerokość włosa, sporządzić wykres natężenia promieniowania I w funkcji kąta ugięcia θ, oraz na tej podstawie obliczyć szerokość szczeliny dyfrakcyjnej. Wszystkie te zadania były oparte na zjawisku dyfrakcji i interferencji światła (w naszym przypadku lasera spójnego i monochromatycznego).

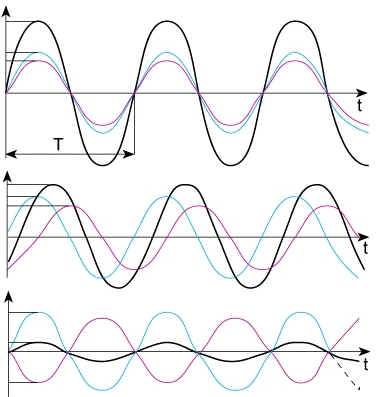
interferencja — wzajemne osłabianie się (niekiedy aż do całkowitego wygaszenia) lub
wzmacnianie 2 lub więcej fal (np. fal świetlnych — interferencja światła)
tej samej częstotliwości wskutek ich nakładania się; pierwszy przypadek
następuje, gdy fazy fal są przeciwne, drugi — gdy zgodne.

dyfrakcja — ugięcie fal, odchylanie się biegu promieni fal (np. świetlnych - dyfrakcja
światła) od prostoliniowości, zachodzące w pobliżu krawędzi ciał
nieprzezroczystych, a także na wąskich (w porównaniu z długością fali)
szczelinach.

Zjawiska te umożliwiają wykonywanie pewnych pomiarów, tak jak w naszym przypadku pomiar grubości włosa (co za pomocą tradycyjnych metod raczej nie jest wykonalne). Zadanie to polegało na ustawieniu włosa na linii źródło lasera - ekran (odległość włosa od ekranu: 1005mm). Potem korzystając z widma otrzymanego na ekranie i z odpowiednich wzorów należało obliczyć szukaną wielkość. Zostało tutaj użyte światło lasera dlatego, że jest ono monochromatyczne, spójne i o stałej określonej długości, co powoduje, że interferencje i dyfrakcje tego światła na włosie są niezmienne w czasie, co umożliwia obserwację prążków interferencyjnych, inaczej minimów, czyli miejsc, gdzie fale bliźniacze zachodzą na siebie redukując się (w przypadku lasera, do zera). Dzięki temu zjawisku można było wykonać podane wyżej ćwiczenia. Do obliczenia szerokości włosa wykorzystujemy istnienie tychże prążków, na podstawie wzoru:

gdzie:

a — szukana szerokość włosa

L — odległość włosa od ekranu (1005mm)

m — ilość minimów branych pod uwagę przy obliczeniach (7)

y_m — odległość m-tego minimum do miejsca padania wiązki na ekran

λ — długość światła lasera (czerwone: 632,8 mm)

skąd wynika:

Czyli szerokość włosa wynosi 6,27*10^-5m.

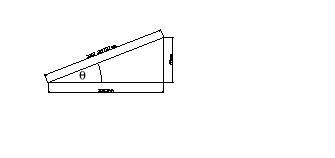
Drugim zadaniem było na 2 sposoby zmierzyć szerokość szczeliny dyfrakcyjnej. Pierwszy z nich polegał na znalezieniu jej z zależności geometrycznych opartych na twierdzeniu Pitagorasa (skąd otrzymujemy przeciwprostokątną - odległość minimum od źródła dla m=15 y₁₅=68mm).

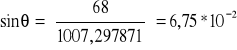
Potem korzystając z funkcji trygonometrycznych i powyższej zależności wyznaczmy kąt ugięcia fali:

Następnie korzystając z odpowiedniego wzoru

obliczamy szukaną szerokość szczeliny dyfrakcyjnej.

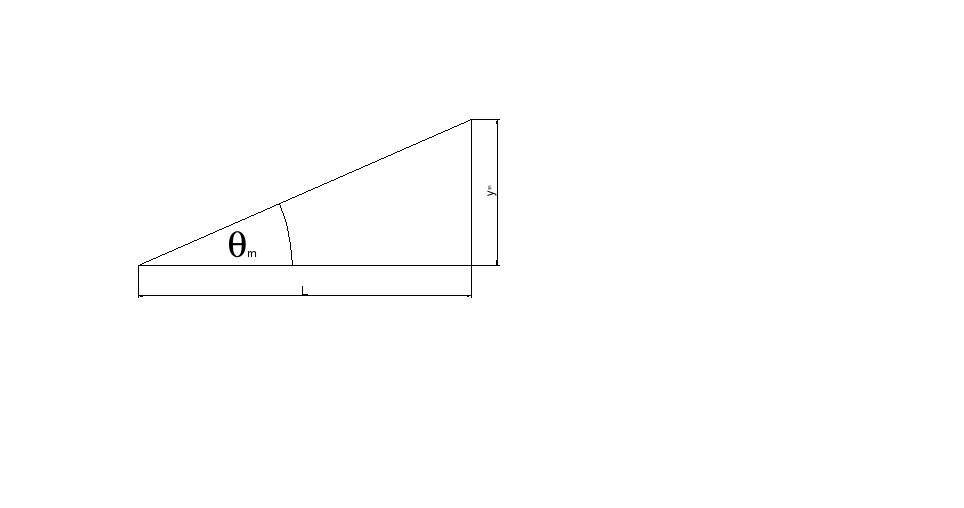
Druga metoda obliczenia tego wymiaru opiera się na wykresie zależności natężenia promieniowania I w funkcji kąta ugięcia θ (w załączeniu oraz rys.1). Sporządzony on został na podstawie pomiaru natężenia prądu oraz z odległości kolejnych minimów i maksimów dyfrakcyjnych od środka ekranu. Kąty ugięcia fali kolejnych maksimów i minimów obliczamy z prostej zależności w trójkącie prostokątnym:

gdzie

θ_m — kąt ugięcia fali dla m-tego minimum lub maksimum

y_m — odległość m-tego minimum lub maksimum od środka ekranu

L — odległość szczeliny od ekranu

skąd wynikają odpowiednie wartości, gdzie odległości od środka ekranu są przeliczone z pewnych odczytów ze śruby mikrometrycznej poruszającej fotoelementem (fotodiodą):

Lp	MAKSIMA			MINIMA
		Natężenie I z fotoelementu	odległość od środka	kąt odchylenia	Natężenie I z fotoelementu	odległość od środka	kąt odchylenia
1	1350 μA	0 mm	0º	7,2 μA	4,34 mm	0,25º
2	55 μA	6,14 mm	0,35º	1 μA	8,64 mm	0,49º
3	14,4 μA	10,71 mm	0,61º	0,7 μA	12,79 mm	0,72º

Natężenia prądu dla minimów nigdy nie spadną do zera z dwóch powodów: braku zupełnej ciemności (oświetlenie zewnętrzne), oraz brak nieskończonej oporności dla fotokomórki. Przy założeniu L >> y_m można powiedzieć, że:

czyli:

gdzie

m — nr kolejnego minimum (1 ≤ m ≤ 3)

a_m — m-ty wynik obliczeń szerokości szczeliny

λ — długość fali światła emitowanego przez laser

θ_m — kąt ugięcia m-tego minimum.

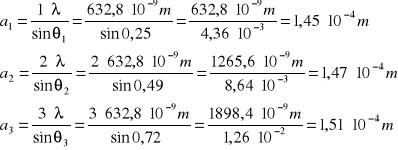
skąd:

Z powyższych wyników należy teraz wyciągnąć średnią arytmetyczną, a potem wyliczyć błąd metodą średniego błędu kwadratowego wartości sumy z uwzględnieniem rozkładu t-Studenta przy stopniu ufności β=0,95, oraz n=3, k=n-1=2.

Ostateczny wynik brzmi:

czyli szczelina dyfrakcyjna ma szerokość (1480 ± 188)*10^-9m, co jest porównywalnym wynikiem (prze co dosyć prawdopodobnym) do wyniku uzyskanego poprzednią metodą, ponieważ mieści się w granicach błędu (1,292*10^-4 m ÷ 1,668*10^-4 m). Można stąd wyciągnąć wniosek taki, że metoda oparta na wykresie jest dokładniejszą. Należy przypuszczać, że metody takie mogą być stosowane w wielu dziedzinach nauki, gdzie wymagane są dość dokładne pomiary małych wymiarów.

4

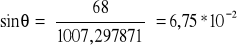
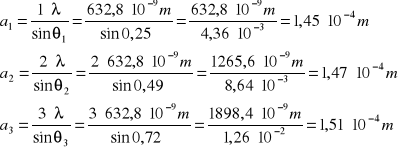
rys.1

---