Uniwersytet Zielonogórski		Metrologia Techniczna Laboratorium
Temat ćwiczenia: Sprawdzenie uniwersalnych narzędzi pomiarowych			Nr tematu : MDK 2031
Imię i nazwisko : Adam Cichowicz	Grupa : 21 B	Data wykonania: 10.05.2009	Zaliczenie :

1.Cel ćwiczenia.

Celem ćwiczenia jest poznanie środków pomiarowych stosowanych przy pomiarach stożków oraz sposobów ich praktycznego wykorzystania, a także przeprowadzenie oceny uzyskania dokładności pomiarów tymi przyrządami

2. Pomiar stożka wewnętrznego o dużej zbieżności i małych średnicach .

Pomiaru średnic kulek dokonano mikrometrem MMZc 0 - 25 mm; wysokości A i B
głębokościomierzem MEBa 300.

2.1. Schemat pomiarowy.

2.2. Wyniki pomiarów.

Pomiary średnic kulek [mm]			Pomiary głębokości [mm]
Lp.	D	d	Lp.	A	B
1	21,42	17,97	1	18,20	27,90
2	21,42	17,97	2	18,20	28,10
3	21,42	17,97	3	18,20	27,90
Śr.	21,42	17,97	Śr.	18,20	27,96

2.3.Obliczenia kąta i błędów pomiaru.

W celu wyznaczenia kąta stożka wykorzystuje się poniższą zależność:

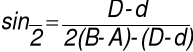
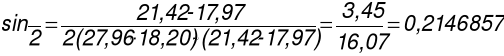
Po obliczeniach otrzymujemy następujące wyniki:

sin /2	/2
0,2146857	12^0 18' 02"	24 ^0 36' 04"

2.4. Analiza błędów

Niepewność pomiaru wynosi :

Dla przyrządów suwmiarkowych x = (50 + 0,1L) [μm]

Dla przyrządów mikrometrycznych x = (4 + L / 50) [μm],

gdzie:

- L - wartość mierzona

D = ± (4 +21,42 / 50) = 4,4284 [m]

d = ± (4 +17,97 / 50) = 4,3592 [m]

A = ± (50 +0,1 × 18,20) = 51,82 [m]

B = ± (50 + 0,1თ× 27,96) = 52,796 [m]

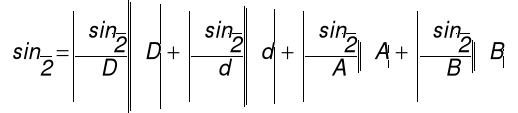
2.5. Błąd bezwzględny maksymalny (graniczny):

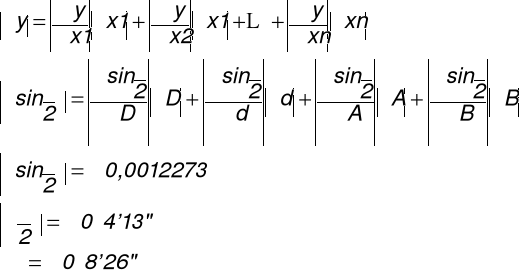
Po uwzględnieniu błędu maksymalnego bezwzględnego otrzymujemy:

Kąt stożka	Niepewność pomiaru kąta	Wynik

3. Pomiar stożka (kata) za pomocą sinuśnicy.

Metoda ta jest stosowana:

• do pomiarów kątów wierzchołkowych stożków i pochyleń przedmiotów o prostych kształtach,

• do pomiaru kątów mniejszych niż 45° ze względu na szybki wzrost błędów pomiaru dla kątów poniżej 45°.

3.1. Schemat pomiarowy

3.2.Wyniki pomiarów.

L = 100 mm,

l = 83 mm,

H = 4,10 mm,

W = - 0,02 mm.

Mierzony kąt wierzchołkowy α określa się ze wzoru:

α = (α_H + α_W)±[|Δα_H + Δα_W|]

gdzie:

α_H - kąt wynikający z przyjętego stosu płytek:

sinα_H =
stąd α_H = arc sin

α_W - kąt wynikający z różnicy wskazań czujnika 0_II i 0_I na odległości l:

sinα_W =
stąd α_W = arc sin

gdzie: w = 0_II - 0_I

Δα_H i Δα_W - niepewności pomiarowe obliczone na podstawie:

Δα_H =

Δα_W = ±

3.3. Obliczenia:

3.3.1. Obliczenie α_H:

sin α_H =
⇒ α_H = arc sin

- H = 4,10 mm,

- L = 100 mm.

α_H = arc sin
= arc sin 0,041 = 2⁰ 20' 56”

3.3.2. Obliczenie α_W:

sinα_W =
⇒ α_W = arc sin

w = 0_II - 0_I

- 0_I = 0 mm,

- 0_II = 0,02 mm

w = 0,02 - 0 = 0,02 mm

l = 83 mm

α_W = arc sin
= arc sin 0,000240963 = 0⁰ 00' 49”

3.3.3. Obliczenie Δα_H :

Δα_H =

gdzie:

α_H - 0,041 (2⁰ 20' 56”)

L - 100 mm,

ΔH - błąd graniczny dopuszczalny długości płytki wzorcowej ; ΔH = ± 0,90μm,

ΔL - dopuszczalne odchyłki wskazań przyrządów suwmiarkowych

ΔL =±(50 + 0,1L) [μm] ;

gdzie:

L - wartość mierzona

ΔL = ±(50 + 0,1⋅100) = 60 μm

Δα_H = ±
= 1⁰ 55' 36”

3.3.4. Obliczenie Δα_W :

Δα_W = ±

gdzie:

α_W - 0,00024- (0° 0' 49”)

l = 83 mm,

Δw - niepewność wskazania czujnika zegarowego; Δw = ± 8 μm,

Δl - dopuszczalne odchyłki wskazań przyrządów suwmiarkowych

Δ=±(50 + 0,1⋅i) [μm]

gdzie l - wartość mierzona

Δi = ±(50 + 0,1⋅83) = 58,3 μm

Δα_W = ±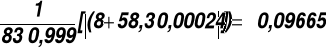
=34⁰33' 34”

α = (α_H + α_W)±[|Δα_H + Δα_W|]

3.3.5. Obliczenie kąta α stożka :

α = (0,041 + 0,00024)±[0,03369 + 0,09665]

α = 0.04124⁰ ± 0,13034°

α = 2⁰ 21'46”± 7⁰ 28' 04”

4. Pomiar stożka wałeczkami o równej średnicy.

Metodę tę stosuje się do pomiaru stożków długich o małej zbieżności C, przy czym stożki tylko te, które można ustawić na płycie mierniczej.

4.1. Schemat pomiarowy

Kąt wierzchołkowy stożka oblicza się ze wzoru:

tg
=

Pomiaru wartości wielkości mierzonych dokonałem mikrometrem MMZc 25 - 50:

4.2. Wyniki pomiarów

Lp.	A	B	H
1	39,93	36,08	75,00
2	39,925	36,09	75,00
3	39,925	36,085	75,00
Śr.	39,927	36,085	75,00

4.3. Obliczenia

Podstawiając do powyższego wzoru otrzymujemy:

tg
=
= 0,025613

tg
= 1⁰ 28' 03”

α = 2⁰ 58' 06”

5. Wnioski.

Celem ćwiczenia było poznanie środków pomiarowych stosowanych przy pomiarach stożków oraz sposobów ich praktycznego wykorzystania, a także przeprowadzenie oceny uzyskania dokładności pomiarów tymi przyrządami. Na podstawie wyników można stwierdzić, że pomiary bezpośrednie są dużo dokładniejsze od pomiarów pośrednich. Zaletą pomiarów pośrednich jest ich łatwość wykonania bez konieczności stosowania skomplikowanych narzędzi pomiarowych. Dokładność pomiarowa przy pomiarach pośrednich, zależy głównie od poprawności działań matematycznych. W miarę możliwości w celu otrzymania dokładnych wyników należy stosować pomiary bezpośrednie, pamiętając jednak o eliminacji błędów grubych.

α/2

HL

α_H

d

D

α / 2

B

A

O_I

O_II

W

α

LL

l

H

B

A

---