Całki powierzchniowe
Obliczyć całki powierzchniowe niezorientowane:
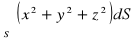
, gdzie S : część płaszczyzny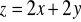
leżąca nad kwadratem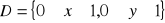
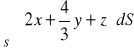
, gdzie S część płaszczyzny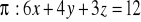
, leżąca w 1. oktancie układu współrzędnych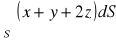
, gdzie S : część płaszczyzny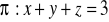
,
,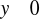
,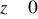
.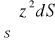
, gdzie S: część stożka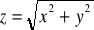
, dla którego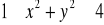
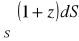
, gdzie S : połowa sfery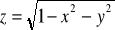
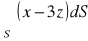
, gdzie S: powierzchnia trójkąta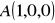
,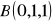
,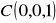
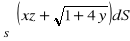
, gdzie S: część powierzchni walca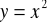
, zawartego między płaszczyznami :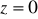
,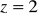
,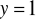
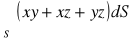
, gdzie S: część powierzchni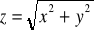
, wyciętej powierzchnią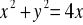
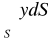
, gdzie S: powierzchnia półkuli :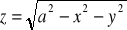
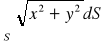
, gdzie S; powierzchnia boczna stożka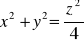
, odcięta płaszczyznami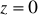
,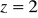
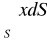
, gdzie S; powierzchnia kuli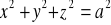
, znajdująca się w 1. oktancie układu współrzędnych.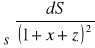
, gdzie S: część powierzchni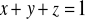
, znajdująca się w 1. oktancie układu współrzędnych.
Obliczyć całkę powierzchniową zorientowaną:
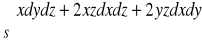
, gdzie S :część płaszczyzny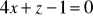
, leżąca nad
: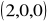
,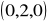
,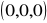
, zorientowana w stronę nie zawierającą środka układu współrzędnych.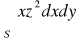
, gdzie S :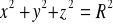
,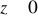
, zorientowana dodatnio.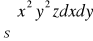
, po górnej stronie dolnej połowy sfery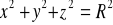
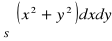
, po dolnej stronie powierzchni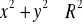
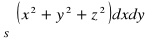
, gdzie S : górna strona powierzchni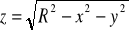
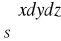
, gdzie S: dodatnia strona części powierzchni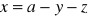
,
leżąca nad trójkątem określonym nierównościami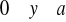
,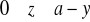
.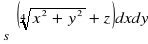
, gdzie S : dolna strona powierzchni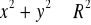
.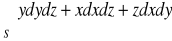
, gdzie S: górna strona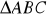
wyciętego przez płaszczyzny układu współrzędnych z płaszczyzny o równaniu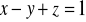
Zastosować tw. Gaussa-Ostrogradzkiego
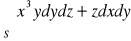
, gdzie S :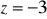
,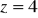
,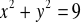
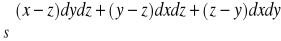
, gdzie S: zewnętrzna strona stożka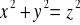
,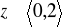
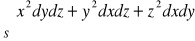
, gdzie S : zewnętrzna strona sześcianu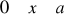
,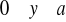
,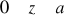
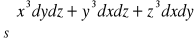
, gdzie S : zewnętrzna strona sfery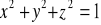
Wyszukiwarka
Podobne podstrony:
Zadania.Calki krzywoliniowe, Oceanotechnika. PG, Semestr 2
Studia Niestacjonarne ZADANIA Z GEOMETRII WYKRESLNEJ, Mechanika i Budowa Maszyn PG, semestr1, Grafik
Zadanie 1 kolokwium 1 2007-08, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
Zadaniasiecdlastudentow, Budownictwo PG, Semestr 5, TiORB, ćwiczenia
Zadanie 3 kolokwium 1 rok2012-13, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kó
Zadanie 2 kolokwium 2 2010-11, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
Egzamin poprawkowy z matematyki rok 2010-2011 zadanie nr 4, Budownictwo PG, Semestr 3, Matematyka, P
Zadanie 5 kolokwium 1 2008-09, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
Zadanie 4 kolokwium 1 2011-12, Budownictwo PG, Semestr 3, Matematyka, Prace domowe-rozwiązania kół
zadania z relatywistyki, Budownictwo PG, Semestr 1, Fizyka, Ściągi, teoria na koła, Zadania, Relatyw
Całki powierzchniowe, zadania
Zadania-lista4, POLITECHNIKA WROCŁAWSKA (2009), Semestr II, Fizyka 2
w 1 - wartość pieniądza w czasie - zadania dodatkowe, wszop ZZIP, II semestr, finanse i rachunkowość
Temat3, Mechanika i Budowa Maszyn PG, semestr 2, Materiałoznawstwo II, laborki
Matematyka Sem 2 Wykład Całki Powierzchniowe
elektrotech test zeszly rok + zadanie na ten test, Uczelnia, semestr2, elektronika
zadania na kolokwium informatyka, gik, semestr 4, informatyka
Zadanie 9, żywienie człowieka i ocena żywności, semestr 1, matematyka
więcej podobnych podstron