Zadanie 9.

Rozwiązanie:

Dane pole obszaru zawiera się nad prostą y=x oraz pod funkcją pierw3(x), a także po prawo od osi 0Y i w górę od osi 0X (pierwsza ćwiartka).

Aby wyliczyć granicę, w których będę liczyć obszar przyrównuję do siebie oba wzory funkcji:

*Dodatkowo dla sprawdzenia liczę wartości funkcji dla punktu zawartego pomiędzy granicami obszaru:

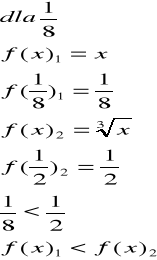
Zatem, rzeczywiście f(x)₁przebiega pod funkcją f(x)₂.

Pole obszaru obliczam z różnicy obszarów pod funkcją 2 i pod funkcją 1.

P_D = P_f2 - P_f1

Pole obszaru pod funkcją to całka oznaczona od dolnej granicy obszaru do górnej granicy obszaru.

Policzę teraz pole pod funkcją 2(niebieskie)

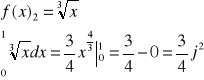
Policzę teraz pole pod funkcją 1 (biorąc pod uwagę, że jest ono trójkątem):

P_f1=(1/2)*|0,1|=(1/2)j²

Oczywiście licząc to jako pole pod całką, dostałabym taką samą wartość.

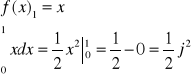
Rzeczywiście, wynik jest ok.

Zatem wyliczone pola podstawiamy do wzoru:

Odpowiedź: Pole jest równe ¼.

f

---