Zadanie 11.
Zanim wykonam dane działania, napiszę trochę teorii.
Minorem odpowiadającym elementowi aik danej macierzy (KWADRATOWEJ!) nazywamy wyznacznik, który powstaje ze skreślenia i-tego wiersza i k-tej kolumny.
Dopełnienie algebraiczne Aik elementu aik nazywamy liczbę równą iloczynowi minora Mik przez (-1)i+k.
Macierz dołączona: jest to taka macierz, w której każdy element aik zastąpimy jego dopełnieniem algebraicznym Aik, a następnie powstałą macierz poddamy transpozycji. Macierz dołączona jest to zatem przestawiona macierz dopełnień algebraicznych.
Macierz odwrotna A-1: jest to taka macierz, która spełnia równości A A-1=I, A-1A=I. Jeżeli macierz kwadratowa jest macierzą nieosobliwą (detA≠0) to istnieje dokładnie jedna macierz odwrotna, która jest równa (równanie z *).
Teraz przedstawię poszczególne wzory i oznaczenia:
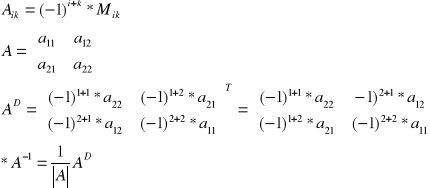
Mnożenie macierzy i transpozycja:
Transpozycja jest to taka operacja, która zamienia wiersze w kolumny i kolumny w wiersze. Przy macierzy symetrycznej zwraca nam tą samą wartość.
Mnożenie macierzy:
Mnożenie macierzy przez macierz określa się wtedy, gdy liczba kolumn pierwszej macierzy jest równa liczbie wierszy drugiej macierzy (wewnętrzne liczby). Przy tej operacji zwracana jest macierz o wymiarach liczby kolumn drugiej macierzy na liczbę wierszy pierwszej macierzy.
Tyle, jeżeli chodzi o teorię. W zadaniu najwyraźniej jest błąd.
Równanie powinno wyglądać (AB-1C)T, ale do tego dojdziemy po wykonaniu pierwszych operacji:
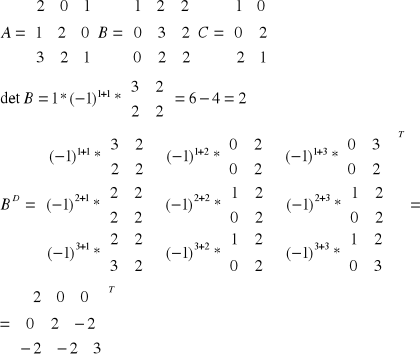
Wyszukiwarka
Podobne podstrony:
Zadanie 10, żywienie człowieka i ocena żywności, semestr 1, matematyka
Zadanie 9, żywienie człowieka i ocena żywności, semestr 1, matematyka
Przykładowe zadania z matematyki, żywienie człowieka i ocena żywności, semestr 1, matematyka
Zadanie 7, żywienie człowieka i ocena żywności, semestr 1, matematyka
Zadanie 6, żywienie człowieka i ocena żywności, semestr 1, matematyka
Zadanie 8, żywienie człowieka i ocena żywności, semestr 1, matematyka
Zadanie 9, żywienie człowieka i ocena żywności, semestr 1, matematyka
sprawozdanie z genetyki 11, żywienie człowieka i ocena żywności, semestr 4, genetyka
wykład biologia 16.11, żywienie człowieka i ocena żywności, semestr 1, biologia
Badanie funkcji, żywienie człowieka i ocena żywności, semestr 1, matematyka
matma calki, żywienie człowieka i ocena żywności, semestr 1, matematyka
Higiena Produkcji - pytania z Zywienia-Diet. - sesja zima200, żywienie człowieka i ocena żywności, s
woda jako składnik żywności oraz równowagi kwasowo- zasadowe w żywności, żywienie człowieka i ocena
pytaniahigienaaa, żywienie człowieka i ocena żywności, semestr 4, higiena
FIZJOLOGIA PYTANIA I TERMIN 2014 dzienne grupa A, żywienie człowieka i ocena żywności, semestr 4, fi
Organizacja wykladen, żywienie człowieka i ocena żywności, semestr 2, organizacja przed
Gary sciaga2, żywienie człowieka i ocena żywności, semestr 4, technologia gastronomiczna
więcej podobnych podstron