I.

Na wyspie Ogao na Pacyfiku odbywa się właśnie doroczne święto, w trakcie którego młodzi członkowie plemienia wybierają na najbliższe lata swojego życia jedno z czterech tradycyjnych zajęć: leczenie ludzi i zwierząt (medyk), wychowywanie i nauczanie (wychowawca), zbieranie żywności (żywiciel) i produkowanie przedmiotów użytkowych (rzemieślnik).

Masz niezwykłą możliwość obserwowania tej uroczystości i postanawiasz zebrać dane na temat tego, jakie zajęcia wybierają chłopcy, a jakie dziewczęta.

Spośród 15 dziewcząt

2 wybrały zawód medyka, 4 żywiciela, 5 wychowawcy, a pozostałe rzemieślnika.

Spośród 13 chłopców

3 wybrało zawód medyka, 2 żywiciela, 4 wychowawcy i pozostali rzemieślnika.

1. Zdefiniuj zmienne, określ poziomy ich pomiaru. Wprowadź dane do edytora. Zapisz plik z danymi.

2. Przeprowadź odpowiednią analizę i odpowiedz na poniższe pytania:

• Jaki procent wszystkich nowych wychowawców stanowią chłopcy?

• Jaki procent wszystkich młodych ludzi wybrał zawód medyka?

• Jaki procent dziewcząt wybrał zawód rzemieślnika?

3. Przygotuj wykres częstości dla zmiennej określającej wybrane zajęcia. Czy i ewentualnie jaką miarę tendencji centralnej można określić dla tej zmiennej?

4. Utwórz zmienną określającą stopień uspołecznienia wybranego zawodu wiedząc, że wynosi od dla medyka - 4 dla wychowawcy - 5, dla rzemieślnika - 2 i dla żywiciela - 2.

II.

W trakcie tej samej uroczystości odbywa się konkurs pływacki w dwóch konkurencjach - pływaniu w morzu i pływaniu w rzece. Oto wyniki w tej konkurencji - czas pokonywania wyznaczonego dystansu w sekundach:

pływanie w morzu - 150 200 180 163 142 195 174 179 193 182 179 172 169 181 159

pływanie w rzece - 150 200 180 163 142 174 178 182 179 172 169 159 155 149 140

1. Zdefiniuj zmienne, określ poziomy ich pomiaru. Wprowadź dane do edytora. Zapisz plik z danymi.

2. Przygotuj wykres częstości dla tej zmiennej. Czy i ewentualnie jakie miary tendencji centralnej i rozproszenia można określić dla tej zmiennej?

3. Podaj te miary dla całej zmiennej oraz osobno dla każdej z konkurencji. Zapisz plik raportu.

III.

Badacze przygotowujący autorski program nauczania z zakresu wiedzy o społeczeństwie zwrócili się do Twojej firmy z prośbą o ustalenie zróżnicowania w zainteresowaniu zagadnieniami politycznymi wśród młodzieży. Podejrzewają, że jednym z ważnych czynników, który może wpływać na konieczność zróżnicowania programu, może być miejsce zamieszkania ucznia, a drugim płeć. Przeprowadzasz badania kwestionariuszem, w którym można uzyskać do 40 punktów (jeden punkt za zgodę z każdym z 40 twierdzeń) i większa ilość punktów wskazuje na wyższe zainteresowanie zagadnieniami politycznymi. Uzyskujesz następujące wyniki:

Wyniki wg miejsca zamieszkania dziewcząt chłopców

miasto do 5000 mieszkańców - 15, 10, 16, 20 20, 10, 12, 14

miasto od 5 do 100 tys. mieszkańców - 25, 18, 32, 28 25, 38, 10, 22

miasto powyżej 100 tys. mieszkańców - 35, 38, 24, 31 22, 27, 39, 35

1. Zdefiniuj zmienne, określ poziomy ich pomiaru. Uzasadnij wybór poziomu pomiaru. Wprowadź dane do edytora. Zapisz plik z danymi.

2. Przeprowadź odpowiednią analizę i odpowiedz na pytania:

• jaki procent wszystkich chłopców uzyskał wynik powyżej 30 punktów?

• jaki procent wszystkich mieszkańców miast powyżej 100 tys. mieszkańców stanowią dziewczęta?

• jaki procent wszystkich osób badanych uzyskał wynik 10 punktów?

3. Utwórz zmienną dzielącą badanych na cztery grupy wg stopnia zainteresowania zagadnieniami politycznymi.

4. Przygotuj wykres częstości dla wyników w kwestionariuszu oraz dla miejsca zamieszkania. Czy i ewentualnie jakie miary tendencji centralnej i rozproszenia można określić dla tych zmiennej? Jakich nie można stosować? Uzasadnij odpowiedź.

5. Podaj charakterystyki rozkładu (miary tendencji centralnej, rozproszenia i odkształcenia od rozkładu normalnego) dla zmiennej wynik w kwestionariuszu osobno dla dziewcząt i chłopców. Zapisz plik raportu.

IV.

Zimbardo, Ruch Psychologia i życie str. 169

Badanym polecono nauczyć się na pamięć kilku słów. Gdy tylko to uczynili, podzielono ich na trzy grupy i każdej z grup dano różną ilość czasu na dodatkowe ćwiczenia. Pierwsza grupa powtarzała słowa przez tyle czasu, ile zajęło ich nauczenie się, druga przez połowę tego czasu, trzecia wcale. Po miesiącu sprawdzono odtworzenie list. Liczba odtworzonych słów wynosiła:

gr. 1 2, 1, 5, 4, 3, 3

gr. 2 4, 3, 6, 5, 4, 5

gr. 3 6, 7, 5, 4, 7, 6

6. Zdefiniuj zmienne, określ poziomy ich pomiaru. Uzasadnij wybór poziomu pomiaru. Wprowadź dane do edytora. Zapisz plik z danymi.

7. Przeprowadź odpowiednią analizę i odpowiedz na pytania:

• jaki procent wszystkich badanych z gr. 1 uzyskał wynik 3?

• jaki procent wszystkich osób które odtworzyły prawidłowo 4 słowa należał do gr. 2?

• jaki procent wszystkich osób badanych odtworzył prawidłowo 5 słów?

8. Utwórz zmienną dzielącą badanych na dwie grupy - tych którzy uczyli się dodatkowo i tych, którzy nie uczyli się dodatkowo.

9. Przygotuj wykres częstości dla liczby odtworzonych słów. Czy i ewentualnie jakie miary tendencji centralnej i rozproszenia można określić dla tych zmiennej? Jakich nie można stosować? Uzasadnij odpowiedź.

10. Podaj charakterystyki rozkładu (miary tendencji centralnej, rozproszenia i odkształcenia od rozkładu normalnego) dla zmiennej liczba odtworzonych słów osobno dla badanych, którzy uczyli się dodatkowo i którzy nie uczyli się dodatkowo. Zapisz plik raportu.

I.

W pewnym szpitalu, na oddziale położniczym, notowano każdego dnia płeć rodzących się dzieci. W powyższej tabeli krzyżowej znajdują się zapiski z jednego tygodnia.

1. Jaki procent chłopców urodził się w czwartek?

2. Jaki procent dzieci urodzonych w poniedziałek stanowią dziewczynki?

3. Jaki procent wszystkich dzieci urodził się w środę?

4. Jaki procent wszystkich dzieci stanowią dziewczynki urodzone we wtorek?

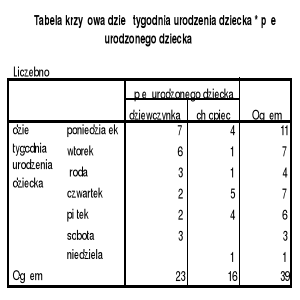
5. Którego dnia urodziło się najwięcej dzieci? Jakiej miary używa się aby odpowiedzieć na to pytanie?

6. Czy można policzyć średnią liczbę urodzeń? Dlaczego?

7. Jaka jest średnia liczba urodzeń chłopców, a jaka dziewczynek?

8. Stwórz nową zmienną, dzielącą dni tygodnia na dwie kategorie: dni robocze i weekend.

9. Zrób wykres urodzeń dla tej nowej zmiennej oddzielnie dla chłopców i dla dziewczynek.

10. Jakie miary tendencji centralnej można policzyć dla tej zmiennej?

11. Jakie miary rozproszenia można policzyć dla tej zmiennej?

II.

W okresie od stycznia do grudnia 2000 roku odnotowano 57 331 wypadków drogowych. W 1999 roku wydarzyło się 55 106 wypadków, zaś w 1998 61 855.

Liczba osób które zostały ranne w tych wypadkach wyniosła 71 638 w roku 2000, 68 449 w 1999 roku i 77 560 w roku 1998.

Liczba ofiar śmiertelnych w wyniku wypadków drogowych: W roku 2000 zginęły 6 294 osoby, w roku 1999 - 6 730, zaś w roku 1998 - 7 080.

1. Stwórz nową zmienną, która będzie określała liczbę ofiar (czyli liczbę rannych i liczbę ofiar śmiertelnych) w wypadkach drogowych w poszczególnych latach.

2. Jaka była największa liczba ofiar? W którym roku? Jak nazywamy zmienną która to określa?

3. Jaka była średnia liczba wypadków drogowych?

4. Jaka była średnia liczba ofiar śmiertelnych?

5. Dlaczego można policzyć średnią dla tej zmiennej?

III.

Królewna Śnieżka wydała ucztę dla 7 krasnoludków, na którą każdy z nich przyprowadził trzech swoich przyjaciół Śnieżka zmierzyła obwód pasa 7 krasnoludków i ich przyjaciół przed ucztą i po uczcie:

krasnoludek		najlepszy przyjaciel krasnoludka		drugi przyjaciel krasnoludka		trzeci przyjaciel krasnoludka
przed	po	przed	po	przed	po	przed	po
30	40	30	30	30	48	30	38
34	44	34	34	34	56	34	46
38	48	38	48	38	44	38	34
42	52	42	52	42	40	42	30
46	56	46	56	46	64	46	54
50	60	50	60	50	52	50	42
54	64	54	64	54	60	54	50

Utwórz nową zmienną wskazującą przyrost obwodu w pasie

• Ile procent ze wszystkich krasnoludków miało przyrost większy niż o 8 cm?

• Ile procent wśród wszystkich uczestników uczty, którym nie przybyło w pasie, stanowią najlepsi przyjaciele krasnoludków a ile trzeci przyjaciele?

• Ile procent ze wszystkich uczestników uczty stanowią drudzy przyjaciele krasnoludków, którym przybyło w pasie?

Zbadaj rozkład zmiennej "przyrost obwodu w pasie". Jakie miary tendencji centralnej, rozproszenia i odkształcenia od rozkładu normalnego można określić dla tej zmiennej?

IV.

1. Jaki stopień zadowolenia ze stanu zdrowia dominuje wśród respondentów?

2. Jaki najniższy stopień zadowolenia ze stanu zdrowia występuje wśród respondentów?

3. Jaki najwyższy stopień zadowolenia ze stanu zdrowia występuje wśród respondentów?

4. Ilu respondentów jest raczej zadowolonych ze stanu zdrowia?

5. Ilu respondentów jest zadowolonych ze stanu zdrowia w dominującym stopniu?

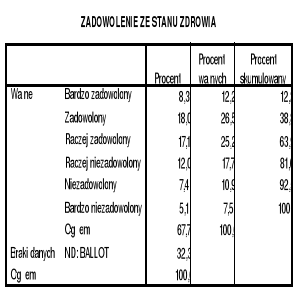
6. Jaka część (%) respondentów udzieliła ważnej odpowiedzi na tej zmiennej?

7. Jaka część (%)respondentów (z ważnymi odp.) jest raczej niezadowolona ze stanu zdrowia lub jeszcze bardziej niezadowolona?

8. Jakie miary tendencji centralnej i rozproszenia można liczyć dla tej zmiennej?

V.

Wykorzystując dane z Kwestionariusza utwórz zmienne:

1. podającą wzrost osoby badanej w metrach

2. podającą wagę osoby badanej w tonach

3. podającą stosunek wzrostu osoby badanej do jej wagi

4. w której wszystkim osobom lubiącym kolory z zakresu czerwieni będzie przypisana wartość 1, osobom lubiącym kolory z zakresu niebieskiego wartość 2; dla pozostałych osób zmienna powinna zwracać systemowy brak danych

5. która podzieli osoby badane pod względem wzrostu na 4 grupy: (a) do 165, (b) 166-170, (c) 171-175, (d) od 176 w górę

Wykonaj analizy częstości dla nowych zmiennych 4 i 5:

1. w całym zbiorze zmiennych

2. w podgrupach wyróżnionych ze względu na płeć (porównaj opcje dostępne w funkcji "podziel na podzbiory"

3. tylko dla osób, które miały ocenę 4 z matematyki na świadectwie

Utwórz zmienną:

w której wszystkim osobom lubiącym kolory z zakresu czerwieni będzie przypisana wartość 1, osobom lubiącym kolory z zakresu niebieskiego wartość 2; dla wszystkich pozostałych osób (również systemowych braków danych) zmienna powinna przyjmować wartość 3.

Wykonaj analizę częstości dla nowej zmiennej oraz płci i odpowiedz na pytania:

4. jaki % kobiet lubi kolory czerwone?

5. jaki % osób lubiących kolory niebieskie to mężczyźni?

6. jaki % wszystkich osób to kobiety lubiące niebieski?

VI.

Jako szkolny psycholog masz ocenić przydatność zaproponowanego twojej szkole treningu dla uczniów. Trening ten dotyczy umiejętności uczenia się i samowzmacniania i ma prowadzić do polepszenia wyników w nauce. Decydujesz się na przetestowanie treningu na grupie uczniów. 10 z nich uczestniczy w treningu, a 10 nie. Porównujesz ich wyniki w nauce (średnią ocen) na koniec semestru przed treningiem (dalej: 1 semestr) i na koniec semestru po treningu (dalej: 2 semestr).

Uczestnicy treningu
w semestrze przed treningiem	3	3	3,5	4	5	3	3,5	4	4,5	4,5
w semestrze po treningu	3,5	4	3,5	4,5	5	3,5	4	4,5	5	4,5
Studenci bez treningu
w semestrze przed treningiem	3	3	3,5	4	5	3	3,5	4	4,5	4,5
w semestrze po treningu	3	3,5	3,5	4,5	5	2,5	3	4,5	4,5	4

1. Przeprowadź odpowiednią analizę i odpowiedz na pytania:

• jaki procent osoby z oceną bardzo dobrą w 1 semestrze stanowią w każdej z grup?

• jaki procent osób z oceną dostateczną w 1 semestrze stanowią uczestnicy treningu?

• jaki procent całej grupy stanowią osoby z bardzo dobra oceną w 2 semestrze, którzy nie uczestniczyli w treningu?

2. Utwórz zmienną, będącą różnicą między wynikami przed treningiem i po treningu

3. Przygotuj wykres częstości dla zmiennej "różnica ocen". Czy i ewentualnie jakie miary tendencji centralnej i rozproszenia można określić dla tej zmiennej? Jakich nie można stosować? Uzasadnij odpowiedź.

4. Podaj charakterystyki rozkładu (miary tendencji centralnej, rozproszenia i odkształcenia od rozkładu normalnego) dla całej zmiennej oraz osobno dla grup z treningiem i bez. Zapisz plik raportu.

Zastosowanie komputerów; mgr Ewa Lipiec - 2004/2005 semestr zimowy

Zadania do wszystkich ćwiczeń

5. Zdefiniuj zmienne, określ poziomy ich pomiaru. Uzasadnij wybór poziomu pomiaru. Wprowadź dane do edytora. Zapisz plik z danymi.

6. Przeprowadź odpowiednią analizę i odpowiedz na pytania o określenie procenta obserwacji w grupie określonej na podstawie jednej ze zmiennych:

7. Przygotuj wykres częstości dla zmiennej. Czy i ewentualnie jakie miary tendencji centralnej i rozproszenia można określić dla tej zmiennej? Jakich nie można stosować? Uzasadnij odpowiedź.

8. Przygotuj wykres częstości zmiennej dla wybranej grupy obserwacji. Podaj charakterystyki rozkładu (miary tendencji centralnej, rozproszenia i odkształcenia od rozkładu normalnego) dla całej zmiennej oraz osobno dla grup obserwacji. Zapisz plik raportu.

9. Utwórz zmienną na podstawie zmiennej już istniejącej; warianty: a) zamieniając wynik na inny, zgodnie z podanym kluczem; b) dodając stałą do istniejącego już wyniku; c) sumując wartości kilku zmiennych; d) zliczając wystąpienie zadanej wartości w kilku zmiennych.

---