LOGIKA PRAWNICZA

przykładowe zadania

z testu zaliczeniowego

Stosunkiem zachodzącym między zakresami nazw S = nauczyciel oraz P = nie-sportowiec jest stosunek:

1. przeciwieństwa,

2. niezależności,

3. podprzeciwieństwa,

4. krzyżowania się zakresów.

Diagram:

P

S M

przedstawia relację pomiędzy zakresami nazw:

1. S = przedszkolanka, P = nie-kulomiot, M = nie-sportowiec,

2. S = nie-przedszkolanka, P = kulomiot, M = nie-sportowiec,

3. S = muzyk, P = pracownik przedszkola, M = przedszkolanka,

4. S = sportowiec, P = muzyk, M = skrzypek.

Diagram:

S P M

przedstawia relację pomiędzy zakresami nazw:

1. S = trener, P = nie-bilardzista, M = nie-sportowiec,

2. S = nie- trener, P = bilardzista, M = nie-sportowiec,

3. S = nauczyciel, P = pracownik przedszkola, M = trener,

4. S = nauczyciel, P = sportowiec, M = tenisista.

Diagram

P

S M

przedstawia relację pomiędzy zakresami nazw:

1. S = trener, P = nie-bilardzista, M = nie-sportowiec,

2. S = nie- trener, P = bilardzista, M = nie-sportowiec,

3. S = nauczyciel, P = pracownik przedszkola, M = trener,

4. S = nauczyciel, P = sportowiec, M = tenisista.

Nazwa dyrekcja Instytutu Ekonomii i Administracji UJK jest nazwą:

1. zbiorową (kolektywną),

2. jednostkową,

3. ogólną,

4. generalną.

Nazwa najludniejsze miasto w województwie świętokrzyskim jest nazwą:

1. abstrakcyjną,

2. prostą,

3. generalną,

4. ogólną.

Definicja Student jest to osoba ucząca się, mająca więcej niż 18 lat nie jest poprawna, bowiem jest:

1. obarczona błędem hipostazowania,

2. obarczona błędem przesunięcia kategorialnego,

3. definicją za szeroką,

4. definicją za wąską.

Definicja Nauczyciel akademicki jest to osoba pracująca w szkole wyższej nie jest poprawna, bowiem jest:

1. obarczona błędem hipostazowania,

2. obarczona błędem przesunięcia kategorialnego,

3. definicją za szeroką,

4. definicją za wąską.

Rozważyć nazwę student kierunku administracja w UJK w roku akademickim 2009/2010. Podział logiczny tej nazwy stanowią następujące układu nazw:

1. dzieci, starcy, osoby w sile wieku,

2. kobiety, łysi mężczyźni, mężczyźni z brodą

3. blondynki, kobiety o nie-blond włosach, mężczyźni,

4. osoby niższe niż 121cm wzrostu, osoby wyższe niż 236cm wzrostu, pozostałe osoby.

Wyodrębnienie w klasie wszystkich mieszkańców Kielc podzbiorów:

• wszystkich mieszkańców poniżej 35 lat,

• wszystkich mieszkańców powyżej 35 lat,

• wszystkich mieszkańców urodzonych poza Kielcami,

nie stanowi podziału logicznego, albowiem:

1. spełnia warunek rozłączności, ale nie spełnia warunku zupełności,

2. spełnia warunek zupełności, ale nie spełnia warunku rozłączności,

3. nie spełnia ani warunku rozłączności, ani warunku zupełności,

4. nie spełnia warunku niepustości wyodrębnionych podzbiorów.

Wyodrębnienie w klasie wszystkich roślin podzbiorów:

• roślin iglastych,

• drzew,

• kwiatów balkonowych

nie stanowi podziału logicznego, albowiem:

1. nie spełnia ani warunku rozłączności, ani warunku zupełności,

2. spełnia warunek rozłączności, ale nie spełnia warunku zupełności,

3. spełnia warunek zupełności, ale nie spełnia warunku rozłączności,

4. nie spełnia warunku niepustości wyodrębnionych podzbiorów.

Zdanie Ślimak jest ssakiem jest zdaniem:

1. analitycznym,

2. subsumpcyjnym,

3. logicznym,

4. wewnętrznie kontradyktorycznym.

Zdanie Żaden wieloryb nie jest urzędnikiem jest zdaniem:

1. atomicznym,

2. ogólnoprzeczącym,

3. szczegółowoprzeczącym,

4. wewnętrznie kontradyktorycznym.

Spójnik międzyzdaniowy ani … , ani … określa się mianem:

1. dysjunkcji,

1. binegacji,

2. dwuargumentowego verum,

3. koniunkcji.

Spójnik międzyzdaniowy jedno z dwojga … , … określa się mianem:

1. koniunkcji,

2. binegacji,

3. alternatywy rozłącznej,

4. dysjunkcji.

Spójnik międzyzdaniowy Co najwyżej jedno z dwojga … , … określa się mianem:

1. dysjunkcji,

2. koniunkcji,

3. alternatywy rozłącznej,

4. binegacji.

Zwrot:

1. ani …, ani …,

2. …, ponieważ …,

3. … mimo to, że …,

4. … lub …   .

jest funktorem intensjonalnym.

Zdanie z funkcji zdaniowej można utworzyć przez:

1. konkretyzację,

2. rugowanie zmiennych,

3. kontrapozycję,

4. kwantyfikację.

Posiadanie samochodu tej samej marki jest relacją:

1. zwrotną,

2. równoważnościową,

3. porządkującą,

4. antysymetryczną.

Podziału logicznego zbioru można dokonać przy pomocy relacji:

1. zwrotnej,

2. równoważnościowej,

3. porządkującej,

4. antysymetrycznej.

Posiadanie wyższego wzrostu jest relacją:

1. przechodnią,

2. równoważnościową,

3. porządkującą,

4. antysymetryczną.

Konwersem relacji bycia matką jest relacja:

1. bycia synem pewnej kobiety,

2. bycia córką,

3. bycia dzieckiem pewnej kobiety,

4. bycia dzieckiem.

Jeśli x jest córką y, to wówczas:

1. y jest ojcem x,

2. y jest matką mężczyzny x,

3. y jest ojcem kobiety x,

4. y jest rodzicem kobiety x.

Wyrażenie
jest schematem, który:

1. nazywany jest prawem wyłączonego środka,

2. jest schematem wyłącznie zdań prawdziwych,

3. jest tautologią,

4. jest zdaniem prawdziwym.

Równoważne wyrażeniu:
jest wyrażenie:

1. 
   ,

2. 
   ,

3. 
   ,

4. 
   .

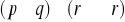
Funkcja zdaniowa
jest schematem wyrażeń:

1. Jeżeli x jest ojcem Jana, to x jest młodszy od Jana,

2. Jeżeli x jest dłużnikiem Pawła, to x unika Pawła,

3. Jeżeli x jest dzielnikiem 15, to x > 15,

4. Jeżeli 3 jest dzielnikiem 15, to 3 < 15.

Funkcja zdaniowa
jest schematem wyrażeń:

1. Wszystkie drzewa mają liście.

2. Każdy urodzony w 21. wieku jest młodszy od Adama Małysza,

3. Jeżeli x jest ojcem Jana, to x jest starszy od Jana,

4. Każda liczba całkowita jest podzielna przez 23.

Funkcja zdaniowa
jest schematem wyrażeń:

1. Wszystkie drzewa mają liście.

2. Istnieje ktoś, kto jest ojcem Jana,

3. Jeżeli x jest ojcem Jana, to x jest starszy od Jana,

4. Niektóre liczby całkowite są podzielne przez 7.

Funkcja zdaniowa
jest schematem wyrażeń:

1. Wszystkie drzewa mają liście.

2. Wszystko ma swoją przyczynę,

3. Jeżeli x jest ojcem y, to x jest starszy od y,

4. Każdy pracownik ma swoje stanowisko pracy.

Alina stwierdziła, że w torebce nie ma jej kart kredytowych, które zawsze tam nosi. Wywnioskowała z tego, że została okradziona w autobusie, którym jechała.

Jest to przykład wnioskowania:

1. uprawdopodobniającego,

2. przez analogię,

3. zawodnego,

4. dedukcyjnego.

Alina po wyjściu z pracy stwierdziła, że jej samochodu nie ma na parkingu. Wywnioskowała z tego, że jej mąż wziął samochód, aby zabrać dzieci ze szkoły.

Jest to przykład wnioskowania:

1. przez analogię,

2. uprawdopodobniającego,

3. zawodnego,

4. redukcyjnego.

Wiadomo, że zdanie: Nieprawda, że jeżeli Paweł mieszka w Kielcach, to jeżeli Paweł studiuje administrację, to Paweł nie mieszka w Kielcach jest prawdziwe.

Wówczas prawdziwe są zdania:

1. Paweł studiuje administrację,

2. Paweł nie studiuje,

3. Paweł mieszka w Warszawie,

4. Paweł nie mieszka w Łodzi.

Z przesłanek: Tylko pełnoletni wstępują w związek małżeński oraz Jan się ożenił wynika logicznie wniosek:

1. Jan nie jest pełnoletni;

2. Jan jest pełnoletni;

3. Jan się ożenił;

4. Jan się nie ożenił.

Zadanie: Niektórzy blondyni nie są lekarzami jest równoważne zdaniu:

1. Niektórzy lekarze nie są blondynami,

2. Niektórzy blondyni są lekarzami,

3. Niektórzy nie-blondyni nie są nie-lekarzami,

4. Niektórzy nie-lekarze nie są blondynami.

Zdaniem równoważnym ze zdaniem Niektórzy studenci nie są sportowcami jest:

1. Niektórzy sportowcy nie są studentami,

2. Niektórzy sportowcy są studentami,

3. Nie jest prawdą, że wszyscy studenci są sportowcami,

4. Niektórzy nie-studenci są sportowcami.

Ze zdania Jeżeli Maciej nadużył wczoraj alkoholu, to dzisiaj boli go głowa wynika logicznie zdanie:

1. Maciej nadużył wczoraj alkoholu i dzisiaj boli go głowa,

2. Jeżeli dziś boli Macieja głowa, to znaczy, że wczoraj nadużył alkoholu,

3. Jeżeli dziś Macieja głowa nie boli, to znaczy, że wczoraj nie nadużył alkoholu,

4. Jeżeli Maciej nie nadużył wczoraj alkoholu, to dzisiaj nie boli go głowa.

Niech α i β będą przesłankami, a γ niech będzie wnioskiem. Wnioskowanie to jest obarczone błędem formalnym, jeżeli:

1. α = Jeśli pada deszcz, to ulice są mokre; β = Deszcz nie pada; γ = Ulice nie są mokre;

2. α = Jeśli pada deszcz, to ulice są mokre; β = Ulice są suche; γ = Deszcz nie pada;

3. α = Jeśli pada deszcz, to ulice są mokre; β = Ulice nie są mokre; γ = Deszcz nie pada;

4. α = Jeśli pada deszcz, to ulice są mokre; β = Deszcz pada; γ = Deszcz nie pada;

- 4 -

---