Adrian Standowicz 25.03.2009

I TM Aa

Ćwiczenie 3: Wyznaczanie stosunku C_p/C_V

1. WSTĘP:

1.1. Pierwsza zasada termodynamiki - Zmiana energii wewnętrznej układu zamkniętego jest równa energii,

która przepływa przez jego granice na sposób ciepła lub pracy.

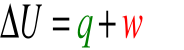
W przypadku układu termodynamicznie izolowanego układ nie wymienia energii z otoczeniem na sposób pracy (w = 0) ani na sposób ciepła (q = 0), wówczas: ΔU = 0

1.2. Ciepło właściwe, ilość ciepła pobranego przez jednostkę masy danego układu powodująca wzrost

temperatury układu o jeden stopień Kelvina (1K). Wyliczamy ją ze wzoru:

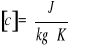
Ciepło właściwe ciał stałych i cieczy jest niezmienną cechą zależną tylko od struktury chemicznej tych ciał. Dla większości substancji zmienia się ono jednak nieznacznie przy zmianie temperatury. Większe zmiany zachodzą podczas zmiany stanu skupienia.

Ciepło właściwe wody: 4189,9
; 76
.

W przypadku gazów ciepło właściwe zależy od rodzaju przemiany gazu, dlatego dla gazów wprowadzono pojęcie ciepła właściwego przy stałym ciśnieniu (c_p) i przy stałej objętości (c_v), które podobnie jak ciepło właściwe ciał stałych i cieczy jest już wartością stałą dla określonych substancji gazowych. C_p i C_v używa się w obliczeniach zależnie od tego czy dana przemiana zachodzi przy stałym ciśnieniu (p.izobaryczna) czy przy stałej objętości gazu (p.izochoryczna).

1.3. Gaz doskonały (g.idealny) - abstrakcyjny, matematyczny model gazu, spełniający następujące warunki:

• brak oddziaływań międzycząsteczkowych (z wyjątkiem odpychania w momencie zderzeń cząsteczek)

• objętość cząsteczek znikoma (punkty materialne) w stosunku do objętości gazu

• zderzenia cząsteczek doskonale sprężyste

• cząsteczki w ciągłym chaotycznym ruchu

Gaz taki w mechanice klasycznej opisuje równanie Clapeyrona (równanie stanu gazu doskonałego), przedstawiające zależność między ciśnieniem gazu (p), jego objętością (V), temperaturą (T) i licznością (n) wyrażoną w molach:

 , gdzie  R jest stałą gazową
, lub

 ,gdzie  k jest stałą Boltzmanna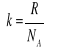
, a N to liczba cząstek w gazie .

Gaz doskonały to model słuszny w pełni jedynie dla bardzo rozrzedzonych gazów. Wzrost ciśnienia powoduje zmniejszenie odległości między cząsteczkami oraz pojawianie się oddziaływań międzycząsteczkowych. Oddziaływania te występują też blisko temperatury skraplania. W bardzo wysokich temperaturach zderzenia przestają być sprężyste. Model ten może być jednak stosowany w praktyce do niemalże wszystkich gazów w warunkach normalnych (p = 1013,25 hPa, T = 273,15 K).

- zależność między pojemnościami cieplnymi:

- wartość pojemności cieplnej przy stałej objętości:

Między wielkościami C_p i C_V zachodzą zależności zwane równaniem Meyera:

1.4. Przemianą gazu doskonałego nazywamy proces zachodzący dla stałej masy gazu. W wyniku procesu

zmianie ulegają pewne parametry stanu gazu, przy czym jeden z parametrów pozostaje stały:

p.izotermiczna (T = const.):

Opisuje ją prawo Boyle'a-Mariotte'a - Dla danej stałej masy gazu iloczyn jego ciśnienia i objętości jest wielkością stałą:

p.izobaryczna (p = const.):

Opisuje ją prawo Guy-Lusaca - Dla danej stałej masy gazu iloraz jego objętości i temperatury

bezwzględnej (wyrażonej w K) jest wielkością stałą:

p.izochoryczna (V = const.)

Opisuje ją prawo Charlesa - Dla danej stałej masy gazu iloraz jego ciśnienia i temperatury

bezwzględnej jest wielkością stałą:

p.adiabatyczna (p, V, T - zmieniają się, ale Q = 0):

, gdzie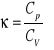
- wykładnik adiabaty

2. TABELA POMIAROWA:

p₀ = 1003 HPa

L.p.	h1 [m]	p1 [hPa]	h2 [m]	p2 [hPa]	κ (x)
1	0,4	1042,24	0,1	1012,81	1,33
2	0,39	1041,26	0,09	1011,83	1,30
3	0,39	1041,26	0,08	1010,85	1,26
4	0,4	1042,24	0,07	1009,87	1,21
5	0,41	1043,22	0,09	1011,83	1,28

3. OBLICZENIA:

Przykład obliczania dla pomiaru 1:

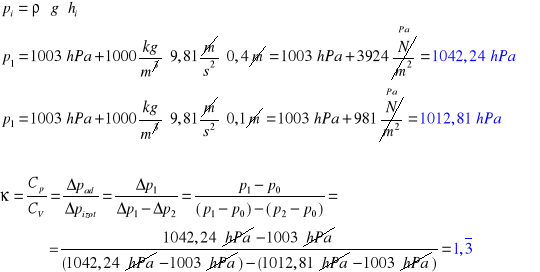
4. RACHUNEK BŁĘDU:

Dane wstępne:

n = 5

α = 0,9

Rachunek błędu (metodą Studenta-Fishera):

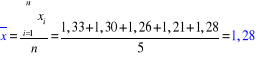
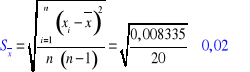
5. WNIOSKI:

Ćwiczenie to pozwoliło nam na poznanie przemiany gazu doskonałego. Oczywiście powietrze to nie gaz doskonały; jest jednak do niego bardzo zbliżone. Dlatego też w naszych rozważaniach potraktowaliśmy powietrze w laboratorium jak gaz doskonały, co uprościło obliczenia, jednak mogło być źródłem nieznacznych błędów.

Porównując nasze wyniki z wartościami tablicowymi, okazuje się, że otrzymaliśmy wyniki zaniżone (wartość tablicowa współczynnika adiabaty powietrza: κ = 1,4). Źródłem błędów w naszym doświadczeniu mogły być takie czynniki jak:

- niedokładny odczyt ciśnienia z barometru i/lub błąd stały tego urządzenia

- niedokładny odczyt różnicy poziomów cieczy

- zbyt wczesne lub zbyt późne zamykanie zaworu zbiornika

- zbyt mocne lub zbyt słabe sprężenie powietrza w początkowej fazie doświadczenia

, gdzie:

ΔU - zmiana energii wewnętrznej układu,

q - energia przekazana do układu jako ciepło,

w - praca wykonana na układzie.

Przyjmujemy przy tym, że gdy:

w > 0 - do układu wpływa energia na sposób pracy,

w < 0 - układ traci energię na sposób pracy,

q > 0 - do układu wpływa energia na sposób ciepła,

q < 0 - układ traci energię na sposób ciepła.

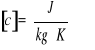
, gdzie:

ΔE - energia potrzebna do ogrzania ciała o określony

przyrost temperatury

Δt - zmiana temperatury

m - masa ciała

c - ciepło właściwe

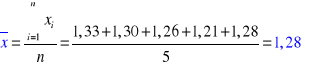
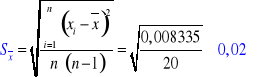
SPRAWOZDANIE

---