Sprawozdanie z fizyki Michał Szewrański

Ćwiczenie nr 56, 57 BLiW

POMIAR INDUKCJI MAGNETYCZNEJ ZA POMOCĄ FLUKSOMETRU

BADANIE ZJAWISKA HALLA

1.Cel ćwiczenia:

• zapoznanie z metodami pomiaru indukcji magnetycznej

• doświadczalna ilustracja zjawiska indukcji elektromagnetycznej i innych zjawisk z pogranicza mechaniki i elektrodynamiki;

• poznanie zjawiska Halla przez pomiary charakterystyki hallotronu i jego praktyczne wykorzystanie;

• poznanie metod pomiaru zmian strumienia indukcji magnetycznej;

2. Podstawy teoretyczne:

2.1. Zasada działania fluksometru.

Wykorzystanie fluksometru ( galwanometru pełznego ) wiąże się z jedną z metod pomiaru pola magnetycznego Instrument ten zbudowany z cewki pomiarowej ( sondy ) oraz specjalnego typu galwanometru spełnia równanie różniczkowe w stosunku do ruchu obrotowego ramki w postaci:

I - moment bezwładności ramki galwanometru;

ϕ - wychylenie kątowe ramki;

r₁ - współczynnik tłumienia mechanicznego;

r₂ = (n₁² B² Q² ) / (R_g+R) - współczynnik tłumienia elektromagnetycznego;

Φ_O = n₁BQ - stała galwanometru;

n₁ - liczba zwojów cewki galwanometru

B - indukcja magnetyczna w szczelinie magnesu galwanometru;

Q - powierzchnia ramki galwanometru;

D moment kierujący nici galwanometru

R - rezystancja zewnętrzna;

R_g - rezystancja wewnętrzna;

Omawiany typ posiada jednak pewne właściwości niezbędne do pomiaru pola magnetycznego upraszczający powyższe równanie:

• nie posiada momentu zwrotnego skąd D = 0;

• pracuje przy małej rezystancji obwodu cewki, a zatem posiada duży współczynnik tłumienia elektromagnetycznego: r₁ +r₂ ≅ r₂;

Stąd uproszczone równanie ruchu ramki : daje po scałkowaniu:

ϕ_K - końcowe wychylenie ramki galwanometru;

q - wartość ładunku;

Ponieważ przepływ ładunku został wywołany impulsem siły elektromotorycznej można zapisać go w postaci równania:

które po scałkowaniu i podstawieniu do równania ruchu ramki daje ostateczny wzór na kąt wychylenia ramki galwanometru:

w którym jak widać nie zależy od wartości prądu i tylko od wartości zmian strumienia indukcji magnetycznej. Cechę tą można wykorzystać do pomiaru natężenia strumienia indukcji zgodnie z równaniem :

n - liczba zwojów sondy;

S - powierzchnia zwoju;

B - indukcja magnetyczna;

2.2. Teoretyczna interpretacja zjawiska Halla.

Płytka z metalu lub półprzewodnika podłączona do prądu o natężeniu I oraz znajdująca się w polu magnetyczny o natężeniu B wytwarza różnicę potencjałów zwaną napięciem Halla na swoich bocznych krawędziach.

Elektrony, które bez obecności pola magnetycznego poruszyłby się z prędkością V_x = I / (enad) wzdłuż kierunku przepływu prądu są w takim przypadku odchylane przez siłę Lorenza zgodnie z równaniem:

F_L = -e (V_x × B);

i koncentrują się na jednej krawędzi płytki, przez co druga posiada ich niedobór.

Powstałe napięcie określa równanie:

; E_y = -F_y / e - powstałe dodatkowe pole elektryczne;

a - szerokość płytki;

d - grubość płytki;

Po podstawieniach otrzymujemy ostateczny wzór na napięcie Halla:

γ = 1 / end - czułość hallotronu;

I - natężenie prądu;

B - natężenie pola magnetycznego;

Zjawiskiem towarzyszący zjawisku Halla jest powstanie prądu asymetrii, przez co na krawędziach bocznych płytki powstaje napięci mimo braku pola magnetycznego. Jest to wynikiem niesymetrycznego ustawienia elektrod hallowskich przy płytce ( różne linie ekwipotencjalne ), ale jednocześnie może być zniwelowane dzięki potencjometrowi kompensacyjnemu zamontowanemu przy hallotronie.

3. Pomiary praktyczne:

3.1. Pomiar indukcji magnetycznej za pomocą fluksometru:

Charakterystyka fluksometru:

• n = 40 - liczba zwojów na cewce fluksometru;

• Δn = 0,5

• S = 4,70 cm² = 0,00047 m² - powierzchnia zwoju;

• ΔS = 0,04 cm² = 0,000004 m²;

Lp.	Ip [ A ]	Φ1 [Wb]	B [T]	ΔB [mT]	δB [%]
1.	0,5	0,0007	0,0372	4,537	0.122
2.	1,0	0,0012	0,0638	3.978	0.062
3.	1,5	0,0017	0,0904	3.419	0.038
4.	2,0	0,0023	0,1223	2.749	0.022
5.	2,5	0,0029	0,1542	2.078	0.013
6.	3,0	0,0034	0,1808	1.519	0.008
7.	3,5	0,0038	0,2021	1.072	0.005
8.	4,0	0,0045	0,2393	0.290	0.001

Obliczenia przykładowe:

T

Otrzymana zależność podana jest na wykresie rys.1.

Dyskusja błędów.

- błąd pomiaru indukcji pola magnetycznego liczymy z różniczki zupełnej:

^*
;

;

• dn = 0,5;

• dS = 0,000004 m²;

• dΦ = 0,0001 Wb - podstawowa działka licznika;

Przykładowe obliczenia:

- punkt 1:

=

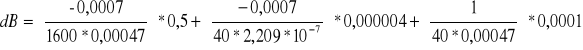
=4,537 mT

δB =

^* obliczenia wykonane różniczką logarytmiczną dają takie same wyniki.

3.2. Pomiar pola magnetycznego hallotronem.

W pierwszym etapie ćwiczenia wyznaczamy zależność napięcia Halla w funkcji indukcji magnetycznej:

U_H = f(B);

Zmieniając wartość natężenia prądu w elektromagnesie ( zmiana pola magnetycznego ) odczytujemy wartości napięcia Halla z licznika V530 (przy stałym I_S = 5V;

Tabelka pomiarów:

Lp.	B [T]	ΔB [T]	I [mA]	ΔI [mA]	UH [V]	ΔUH[V]*10^5	γ	Δγ
1.	0,10	0,002	30	0,75	0,0543	2,71	108,6	3,312
2.	0,15	0,003	44	1,875	0,0796	3,98	106,1	3.236
3.	0,20	0,004	59	1,875	0,1075	5,37	107,5	3.279
4.	0,25	0,005	74	1,875	0,1349	6,74	107,9	3.291
5.	0,30	0,006	89	3,75	0,1645	8,22	109,6	3.343
6.	0,35	0,007	103	3,75	0,1889	9,44	107,9	3.291
7.	0,40	0,008	118	3,75	0,2169	10,84	108,4	3.306
8.	0,45	0,009	133	3,75	0,2435	12,17	108,2	3.3
9.	0,50	0,010	148	3,75	0,2700	13,50	108,0	3.294

Przykładowe obliczenia:

• wartość natężenia charakterystycznego dla danej wartości indukcji magnetycznej odczytujemy z wykresu zależności indukcji od natężenia charakterystycznego dla użytego w pomiarach elektromagnesu;

• błąd pomiaru natężenia obliczamy ze wzoru:

mA - dla pomiaru 1

- dla pomiarów 2-4 zakres = 75; 5-9 zakres 150.

• błąd wartości napięcia Halla obliczamy wykorzystując daną dokładność licznika V530=0,05%:

V;

• błąd wartości indukcji magnetycznej obliczamy wykorzystują dane: ΔB/B = 2%

ΔB = 0,02 * B = 0,02 * 0,1 = 0,002 T;

Wyznaczanie czułości hallotronu:

• 
  ;

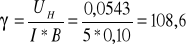
• z różniczki logarytmicznej:
  

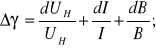
ΔI = 0,05 A

Δγ =

Obliczanie koncentracji elektronów oraz błędów pomiaru:

• γ_sr = 108,29

• Δγ = 3,294

• e = 1,6 * 10^-19 C

• d = 0,0001 m;

n =
;

δn = 12,434 %

Wyznaczanie zależności napięcia Halla od wartości prądu sterującego hallotronem:

U_H = f(I_s):

- przy stałej indukcji magnetycznej odczytujemy wartość napięcia Halla zmieniając wartość prądu sterującego:

Lp.	Is [A]	ΔIs [A]	UH [V}	ΔUH [V}*10^5
1.	1,0	0,05	0,0525	2,625
2.	1,5	0,05	0,0803	4,15
3.	2,0	0,05	0,1103	5,515
4.	2,5	0,05	0,1384	6,920
5.	3,0	0,05	0,1667	8,335
6.	3,5	0,05	0,1958	9,790
7.	4,0	0,05	0,2217	11,085
8.	4,5	0,05	0,2524	12,620
9.	5,0	0,05	0,2770	13,850

- błędy liczone zgodnie ze wzorami podanymi w powyższych obliczeniach;

4. Wnioski końcowe:

W pierwszej części ćwiczenia zapoznaliśmy się ze zjawiskiem Halla poprzez pomiar charakterystyki hallotronu. Zgodnie z teorią napięcie Halla w naszych pomiarach jest proporcjonalne do wartości indukcji magnetycznej, a także do wartości prądu sterującego. Współczynnikiem proporcjonalności jest czułość hallotronu. Ponadto możemy wyznaczyć koncentrację elektronów na krawędzi płytki.

W drugiej części doświadczenia dokonywaliśmy pomiarów strumienia indukcji magnetycznej za pomocą fluksometru. Zależność indukcji magnetycznej od wartości natężenia prądu jest proporcjonalna, choć obarczona pewnymi błędami wynikającymi najprawdopodobniej z niedoskonałości sprzętu, a także krótkiej możliwości odczytu wartości natężenia pola magnetycznego.

1

2

---