KINETYKA - ZADANIA Z PRZYKŁADAMI ROZWIĄZAŃ

1. Obliczyć ile razy wzrośnie stała szybkości reakcji w wyniku ogrzania układu reagującego od temperatury 0°C do temp. 100°C, jeżeli energia aktywacji reakcji jest równa: a) 50 kJ/mol oraz b) 200 kJ/mol.

a)

T₁= 0^oC=273K

T₂= 100_oC=373K

E=50 kJ/mol=50*10³J/mol

R= 8,31 J/mol*K

Korzystając ze wzoru:

wyliczamy:

stąd:

Przykład b) rozwiązujemy analogicznie.

Odp. a) 368,7 b) 1,85*10¹⁰

2. Ile razy zwiększy się stała szybkości reakcji spełniającej regułę van't Hoffa w wyniku ogrzania układu o 100°C, jeżeli temperaturowy współczynnik reakcji jest równy: a) 2, b) 4?

Odp. a) 1024 b) 1048576

3. Badając wpływ temperatury na szybkość rozkładu pewnego środka znieczulającego stwierdzono, że stała szybkości rozkładu tego anestetyka ma wartość 8.6 · 10^-4 h^-1 w temp. 363 K i 21.9 · 10^-4 h^-1 w temp. 373 K. Znaleźć wartość współczynnika temperaturowego Q₁₀ dla tego procesu.

Odp. Q= 2,55

4. Pewna reakcja w temp. 298 K przebiega do końca w czasie 100 min. Obliczyć, w jakiej temp. ta sama reakcja przebiegnie do końca w ciągu 20 min. Współczynnik temperaturowy reakcji Q₁₀ =3.

T₁ =298K

t₁ =100min

t₂ =20min

Regułę van't Hoffa na zależność szybkości reakcji od temperatury można zapisać w postaci:

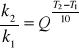
po zlogarytmowaniu:

czyli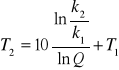

Biorąc pod uwagę, ze dla tej samej reakcji w różnych temperaturach szybkości reakcji są proporcjonalne do ich stałych szybkości, stała k₂ jest 5 razy większą od stałej k₁, podstawiając do wzoru mamy:

T₂= 312,6K

Odp. T₂ = 312,6K

5. Stała szybkości rozkładu N₂O₅
N₂O₄ + ½ O₂ w temp. 273 K wynosi 4.72 · 10^-5 min^-1. Znaleźć okres półtrwania dla tej reakcji oraz ilość N₂O₅ jaka zostanie rozłożona po 20 godzinach. Reakcja jest I rzędu.

k = 4.72 · 10^-5 min^-1=7.86*10^-7 s^-1

T=273 K

T=20h=72000s

T_1/2=

stąd

skoro c_o stanowi początkowe stężenie substancji a więc 100%, aktualne stężenie substratu wynosi c =
i stanowi x%

c_o - 100%

_ x%

x= 94,5%

Czyli przereagowało 100%-94,5%= 5,48%

Odp. T_1/2- 8,8 *10⁵ s ; 5,48%

6. Podczas reakcji hydrolizy 17% roztworu sacharozy w obecności HCl o stężeniu 0.01 mol/l w temp. 308 K otrzymano następujące wyniki:

Czas, min	9,83 59,6 93,2 143 295 589
Niezhydrolizowana sacharoza w %	96,5 80,3 71,0 59,1 32,8 11,1

Oblicz stałą szybkości reakcji.

Odp. k = 6,34 * 10^-5 s^-1

7. Badano szybkość przemiany pewnej substancji A w roztworze. Po 600 s przereagowała połowa początkowej ilości tej substancji. Oblicz, jaka część substancji A pozostanie niezmieniona po 900 s, jeżeli reakcja jest: a) I rzędu, b) II rzędu.

a)

skoro po 600s przereagowała połowa początkowej ilości to T_1/2=600s

k=
=1,155*10^-3s^-1

Znając stałą szybkości reakcji możemy obliczyć ile substancji przereagowało po t=900s

k=

→

stąd:

c= 0,354c_o

czyli po 900s pozostanie 35.46% początkowej ilości substancji.

b)

Korzystając ze wzoru na stałą szybkości reakcji II rzędu:

k=

oraz z przekształcenia wzoru na okres półtrwania:

T_1/2=
→ k=

Otrzymujemy układ równań:

k=

k=

po rozwiązaniu którego otrzymujemy c=0,4c_o,

czyli po 900s pozostanie 40% początkowej ilości substancji .

Odp. a) 35,46% b) 40%

8. Gdyby początkowe stężenie substancji A wynosiło 1.0 mol/l, to w przypadku reakcji I rzędu po 900 s stężenie tej substancji zmniejszyłoby się do 0.353 mol/l. Oblicz czas po upływie którego szybkość reakcji I rzędu A
B zmaleje do połowy w porównaniu z szybkością początkową; k=2· 10^-3 s^-1.

Odp. t= 3,47 * 10² s

9. Stała szybkości reakcji II rzędu rozkładu aldehydu octowego w fazie gazowej wzrasta od 0,105 mol^-1s^-1 w temp. 759 K do 0,343 mol^-1s^-1 w temp. 791 K. Oblicz E_a tej reakcji oraz przypuszczalną stałą szybkości w temp. 836 K.

k₁=0,105 mol^-1s^-1

T₁=759 K

k₂=0,343 mol^-1s^-1

T₂=791 K

Korzystając z równania:

wyliczamy E:

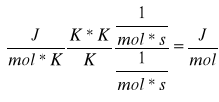
E= 1,845*10⁵ J/mol

Przypuszczalna stałą szybkości k₃ w temperaturze T₃= 836 K obliczamy korzystając z tego samego wzoru, co powyżej, rozwiązując układ równań:

stąd k₃= 1,55 mol^-1s^-1

Odp. E= 1,845*10⁵ J/mol ; k₃=1,55 mol^-1s^-1

10. Zakładając, że cząsteczka A reaguje jednostopniowo z dwoma cząsteczkami B tworząc AB₂ oblicz czemu równa się stała szybkości tej reakcji jeżeli początkowa szybkość powstawania AB₂ wynosi 2,0· 10^-5 mol l^-1s^-1 oraz początkowe stężenie A i B wynoszą 0,3 mol/l.

Odp. k= 7,41*10^-4 l²mol^-2s^-1

11. Wiadomo, że penicylina G (benzylopenicylina) jest nietrwała w środowisku kwaśnym, ponieważ ulega hydrolizie. Niemniej jednak matka życzy sobie, aby tabletki penicyliny G rozkruszyć i podać dziecku w soku pomarańczowym. Oblicz jaki ułamek dawki otrzyma dziecko, jeżeli proces przygotowywania roztworu trwa 2 minuty, a τ_1/2 dla procesu hydrolizy (reakcja I rzędu) ma wartość 3,5 min.

t= 2min=120s

T _1/2=3,5 min= 210s

Proces hydrolizy jest procesem I rzędu a wiec:

stąd wyliczamy k= 3,3*10^-3mol^-1s^-1

Korzystając z wzoru:

wyliczamy:

c=0,673c_o

Czyli dziecko otrzyma ułamek równy 0,673 początkowej dawki leku.

Odp. x = 0,673

12. Rozwiązać ten sam problem (zad.11) dla sytuacji, w której tabletki rozpuszczono o godz. 8:00, a lek podawano przez cały dzień. Ile penicyliny było w tym roztworze o godz. 18:00?

Odp. x=2,54*10^-52

13. Jeden z sulfonamidów traci swoje właściwości terapeutyczne, gdy zawartość substancji czynnej zmaleje o 30 %. Początkowe stężenie badanej próbki tego leku było równe 5 mg/l, a po upływie 20 miesięcy zmalało o 4,2 mg/l. Obliczyć czas dopuszczalnego przechowywania tego leku wiedząc, że proces rozkładu jest procesem I rzędu.

Odp. t=41 miesięcy

14. Rozkład związku A jest procesem I rzędu, którego E_a = 52,3 kJ/mol. W temp. 283 K 10% roztwór tego związku ulega rozkładowi w 10% w ciągu 10 min. W jakim stopniu (w ilu procentach) ulega rozkładowi 20% roztwór tego związku w temp. 293 K.

Odp. 20 %

15. Szybkość tworzenia NO w reakcji:
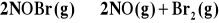
    , wynosi 1,6*10^-5mol/l*s. Jaka jest szybkość zaniku NOBr i szybkość reakcji powst.Br₂?

Odp. d[NOBr]/dt= 1,6*10^-5mol/l*s d[Br₂]/dt=8*10^-6 mol/l*s

16. Szybkość zużywania rodników CH₃^* w reakcji tworzenia etanu zgodnie z równaniem reakcji 2CH₃^*(g)= CH₃CH₃ w pewnych warunkach wynosi 2,4 mol/dm³s. Jaka jest w tych warunkach szybkość tworzenia etanu?

Odp. d[CH₃CH₃]/dt= 1,2 mol/l*s

17. Reakcję aminokwasu tyrozyny (Tyr) z jodem opisuje równanie kinetyczne: V=k[J₂][Tyr]. Jaki jest rząd reakcji ze względu na aminokwas, jod oraz całkowitą rzędowość reakcji.

18. Ile razy zwiększy się stała szybkości reakcji spełniającej regułę van't Hoffa w wyniku ogrzania układu o 100 K, jeżeli współczynnik temperaturowy jest równy 2 i 4.

Q=2

ΔT=100^oK

Regułę van't Hoffa na zależność szybkości reakcji od temperatury można zapisać w postaci:

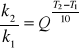
po zlogarytmowaniu otrzymujemy:

stąd:

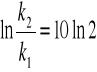
Przykład b) analogicznie.

Odp. a) 1024 b) 1048576

19. Pewna reakcja przebiega w temperaturze 300 K w ciągu 100 min. W jakiej temperaturze ta sama reakcja przebiegnie w ciągu 10 min, współczynnik temperaturowy dla tej reakcji wynosi 3.

Odp T₂ = 320,96 K

21. Stała szybkość rozkładu pewnej substancji w temperaturze 370K wynosi 8*10^-4min^-1, natomiast w temperaturze 390K wynosi 30,3*10^-4min^-1. Jaka jest energia aktywacji i współczynnik temperaturowy tej reakcji.

Odp. E= 7,98*10⁴ J/mol ; Q=1,94

22. Badając utlenienie etanolu katalizowane dehydrogenazą alkoholową, stwierdzono, że jest to reakcja pierwszego rzędu i że stężenie alkoholu maleje z 220 mmol/dm³ do 56 mmol/dm³ po 1,22*10⁴ s. Wyznacz stałą szybkości reakcji.

Odp. k = 1,12*10^-4 s^-1

23. W kwaśnym roztworze wodnym sacharoza rozkłada się na: glukozę i fruktozę w reakcji pseudopierwszego rzędu. W pewnych warunkach (pH i temperatura) czas połowicznego zaniku wynosi 30 min. Ile czasu potrzeba, aby stężenie sacharozy w roztworze zmalało z 10 mmol/l do 1 mmol/l?

Odp. t = 5,98*10³ s

24. Substancja A reaguje dając w dwóch równoległych reakcjach o stałych szybkości k₁ i k₂ dwa produkty B i C. Stosunek stężeń tych produktów w mieszaninie poreakcyjnej wynosi w temperaturze 300K c_B/c_C=2, a w temperaturze 350K c_B/c_C=6. Jaka jest różnica energii aktywacji obu reakcji?

Skoro mamy do czynienia z reakcjami równoległymi to produkty będą powstawać z

szybkością proporcjonalną do stałych szybkości. A wiec

T₁=300K

T₂=350K

=2

=6

ΔE= E_B-E_C= 2,303R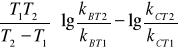

Pamiętając, że

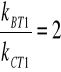
ΔE= E_B-E_C= 2,303R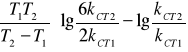

∆E=19167,32 J/mol

Odp. ΔE = 19167,32 J/mol

25. Stała szybkości I rzędowej reakcji konwersji cyklopropanu do cyklopropenu w temp. 400 ⁰C wynosi 1.16 · 10^-6 s^-1 a początkowe stęż. substratu wynosi 1.00· 10^-2 mol/l. Jakie będzie stężenie tej substancji po 24 godzinach?

Odp. 9,045*10^-3 mol/l

---