Nr ćwiczenia	Temat ćwiczenia				Ocena z teorii
9	Współczynnik załamania ciał stałych
Nr zespołu	Nazwisko i imię				Ocena zal. ćwiczenia:
6	Lesiak Michał
Data	Wydział	Rok	Grupa		Uwagi:
23 III 2006	EAI i E	I	3

Cel ćwiczenia

Wyznaczenie współczynnika załamania ciał stałych za pomocą mikroskopu.

Opracowanie teoretyczne:

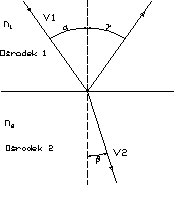
Prawo odbicia

Promień padający, odbity i normalna do powierzchni odbicia są współpłaszczyznowe. Dodatkowo, kąt padania jest równy kątowi odbicia.

Zasada Huygensa

Wszystkie punkty czoła fali można uważać za źródła nowych fal kulistych. Położenie czoła fali po czasie t będzie dane przez powierzchnię styczną do tych fal kulistych.

Dyspersja

Dyspersja jest to zjawisko zależności prędkości fali świetlnej od współczynnika załamania tego ośrodka oraz od częstotliwości drgań przechodzącej fali. Wraz ze wzrostem częstotliwości fali maleje jej prędkość, a rośnie współczynnik załamania.

Dyspersja anomalna - Dla każdego materiału istnieje jednak pewien zakres długości fali, w którym współczynnik załamania maleje. Zakres ten zwany jest obszarem dyspersji anomalnej

Całkowite wewnętrzne odbicie

Jest to zjawisko w którym nie zachodzi załamanie fali na powierzchni łamiącej. Zachodzi ono, gdy kąt padający jest większy od kąta granicznego Θ_g, danego wzorem:

Współczynnik załamania

Gdy wiązka światła przechodzi przez dwa ośrodki o różnych własnościach optycznych, to na powierzchni granicznej częściowo zostaje odbita a częściowo przechodzi do drugiego środowiska, ulegając załamaniu (refrakcji).

Ilustracja 1 Załamanie promienia świetlnego.

Prawo załamania rządzące załamaniem światła zostało sformułowane przez Snelliusa w XII wieku.

Ma ono następującą postać :

gdzie  jest kątem padania światła na płaszczyznę, a  jest kątem załamanej wiązki światła. Obydwa kąty leżą na jednej płaszczyźnie i są mierzone względem prostej normalnej (N) do tej płaszczyzny.

Wielkość n jest stałą, zwaną współczynnikiem załamania ośrodka 2 względem ośrodka 1. Współczynnik załamania zależy od długości fali światła padającego. Z tego względu załamanie może być wykorzystane do rozłożenia wiązki światła na składowe o różnych długościach fali.

Wskutek załamania światła odległości przedmiotów umieszczonych w środowisku w którym prędkość rozchodzenia się światła jest mniejsza wydają się mniejsze. Np. przedmioty w wodzie wydają się mniejsze i bliższe powierzchni. Zjawisko to można prześledzić analizując bieg promienia w płytce płaskorównoległej (poniżej).

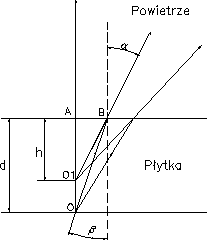
Promień OA prostopadły do powierzchni granicznej wychodzi bez załamania, natomiast OB tworzy z normalną wewnątrz szkła kąt , a w powietrzu kąt , większy od  wskutek załamania. Obserwowane promienie wychodzące z płytki są rozbieżne, ich przedłużenia przecinają się w punkcie O_1­ tworząc obraz pozorny. Odległość O₁A równa h stanowi pozorną grubość płytki, podczas, gdy AO = d jest grubością rzeczywistą.

Ponieważ
a dla małych kątów

widać z rysunku, że (1)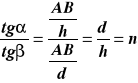
.

Opracowanie wyników

1. Obliczam wartości średnie wskazań czujnika przy ustawieniach mikroskopu na ostrość górnej i dolnej powierzchni.

2. Obliczam grubość pozorną, a następnie współczynnik załamania (n = D / (d₁ - d₂) ).

3. Obliczam błąd średni kwadratowy wartości średniej odczytu ostrości powierzchni górnej i dolnej, a następnie błąd grubości pozornej. Korzystam ze wzoru:

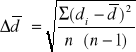
4. Obliczam błąd wyznaczenia współczynnika załamania metodą pochodnej logarytmicznej:

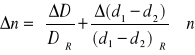
SZKŁO	d1 [mm]	d2 [mm]	d1-d2 [mm]	grubość D [mm]	n
	8,61	5,91	2,70	4,11	1,52
	8,61	5,92	2,69	4,11	1,53
	8,56	5,88	2,68	4,12	1,54
	8,51	5,84	2,67	4,12	1,54
	8,55	5,89	2,66	4,12	1,55
	8,54	5,89	2,65	4,11	1,55
	8,65	5,87	2,78	4,11	1,48
	8,67	5,85	2,82	4,11	1,46
	8,56	5,92	2,64	4,11	1,56
średnia	8,58	5,89	2,70	4,11	1,52
błąd śr. kwadratowy	0,02	0,01	0,02

Wyniki dla obliczeń dla punktów 1, 2 i 3 umieszczone są w tabelce.

4.

ΔD = 0,01 mm, Δ(d₁-d₂) = 0,0206174 mm

W tabelce zamieściłem wartości zaokrąglone, lecz do obliczeń używam wartości dokładnych.

Błąd bezwzględny: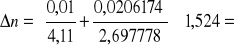
0,015354435 ≈0,02 [mm]

Błąd względny: Δn/n ≈1,01%

Wynik: n = 1,52 ± 0,02 mm

Współczynnik tablicowy dla szkła lekkiego: 1,515

Pleksi 1	d1 [mm]	d2 [mm]	d1-d2 [mm]	grubość D [mm]	n
	8,59	5,75	2,84	4,21	1,48
	8,61	5,73	2,88	4,20	1,46
	8,59	5,775	2,81	4,19	1,49
	8,62	5,76	2,86	4,20	1,47
	8,57	5,77	2,80	4,20	1,50
	8,64	5,77	2,87	4,20	1,46
	8,64	5,73	2,91	4,20	1,44
	8,58	5,8	2,78	4,20	1,51
	8,57	5,75	2,82	4,20	1,49
średnia	8,60	5,76	2,84	4,20	1,48
błąd śr. kwadratowy	0,01	0,01	0,01

Analogicznie:

ΔD = 0,01 mm, Δ(d₁-d₂) = 0,01408747 mm

Błąd bezwzględny: Δn = 0,010849781 ≈ 0,01 [mm]
Błąd względny: Δn/n ≈ 0,73%

Wynik: n= 1,48 ± 0,01 mm

Współczynnik tablicowy dla pleksiglasu: n = 1.492

Pleksi 2	d1 [mm]	d2 [mm]	d1-d2 [mm]	grubość D [mm]	n
	9,12	7,77	1,35	2,17	1,61
	9,19	7,76	1,43	2,17	1,52
	9,18	7,74	1,44	2,18	1,51
	9,14	7,765	1,38	2,18	1,59
	9,21	7,79	1,42	2,19	1,54
	9,21	7,79	1,42	2,18	1,54
	9,20	7,73	1,47	2,18	1,48
	9,26	7,79	1,47	2,18	1,48
	9,22	7,81	1,41	2,18	1,55
średnia	9,19	7,77	1,42	2,18	1,53
błąd śr. kwadratowy	0,01	0,01	0,01

ΔD = 0,01 mm, Δ(d₁-d₂) = 0,01318786 mm

Błąd bezwzględny: Δn = 0,021278945 ≈ 0,02 [mm]

Błąd względny: Δn/n ≈ 1,39%

Wynik: n= 1,53 ± 0,02 mm

Współczynnik tablicowy dla pleksiglasu: n = 1.492

5. Zależność współczynnika załamania od długości fali można wyznaczyć mierząc kąty odchylenia poszczególnych barw światła rozszczepionego w pryzmacie.

Wnioski:

Wartości współczynników załamania dla płytek pleksiglasowych różnią się o 0.05, chociaż teoretycznie wynik powinien być zgodny. Gdyby wziąć pod uwagę wyliczony błąd to różnica wynosi 0.02, a więc nie jest zbyt duża. Błędy pomiarowe mogły wyniknąć z trudności w ocenie ostrości obrazu - dla kolegi była zawsze 0,1mm płytsza/grubsza.

Dla szkła wartość tablicowa współczynnika załamania zgadza się z wartością zmierzoną, co świadczy o poprawności metody.
Dla cieńszej płytki pleksiglasowej wartość tablicowa mieści się w granicach błędu.

Dla grubszej płytki pleksiglasowej tylko dwa pomiary odpowiadały tablicowej wartości. Dość niewielki błąd względny (1,39%) wskazuje prawdopodobnie na to, że to szkło akrylowe (w miejscach obserwowanych na mikroskopie) miało mniejszą zawartość metakrylanu metylu niż cieńsze szkło akrylowe.

Metoda wyznaczania współczynnika załamania dla ciał stałych użytego w tym ćwiczeniu daje szybkie rezultaty i łatwe przeliczenia, a jednocześnie jest precyzyjna - pozwala osiągnąć satysfakcjonujące wyniki.

---