Algorytmy i metody numeryczne

Ćwiczenie Nr 5

CAŁKOWANIE FUNKCJI - METODY KLASYCZNE

Całkowanie numeryczne w MATLAB-ie

MATLAB pozwala na wykonywanie całkowania i różniczkowania metodami nume­rycznymi. Biblioteka Symbolic Math Toolbox umożliwia przekształcanie wyrażeń matematycznych w postaci symbolicznej, w tym całkowanie.

W MATLAB-ie są wbudowane funkcje całkowania numerycznego:

quad - całkowanie metodą adaptacyjną Simpsona

quadl - całkowanie metodą adaptacyjną Lobatto

dblquad - obliczanie całek podwójnych

triplequad - obliczanie całek potrójnych

trapz - całkowanie metodą trapeżów

Funkcja quad

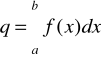
q = quad(fun,a,b)

q = quad(fun,a,b,tol)

fun - funkcja podcałkowa

a,b - granice całkowania

tol - żądana dokładność (względna i bezwzględna)

Przykłady.

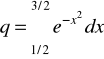
Funkcja, obliczająca funkcję podcałkową dla danego x:

function y=erfcousin(x);

y=exp(-x.^2);

y=quad(`erfcousin',1/2,3/2) ;

Funkcja może być inline objektem

F = inline('1./(x.^3-2*x-5)');

Q = quad(F,0,2);

Q = quad(@myfun,0,2);

myfun.m jest M-plikiem.

function y = myfun(x)

y = 1./(x.^3-2*x-5);

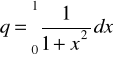
Funkcję podcałkową zapisano do M-pliku funkcyjnego.

% funkcja podcałkowa, plik: fun4i.m

function y = fun4i(x)

y = 1./(1+ x.^2);

Wartość całki obliczono za pomocą funkcji quad oraz quadl.

qa= pi/4 % rozwiązanie dokładne

qa = 0.78539816339745

q1= quad(`fun4i',0,1) % metoda Simpsona

q1 = 0.78539812561468

q2= quadl(`fun4i'\0,l, [le-5 le-4]) % metoda Lobatto

q2 = 0.78539817675805

q3= quadl(@fun4i,0,l, [le-5 le-4]) % użyto function handle @fun4i

q3 = 0.78539817675805

Całkowanie podwójne

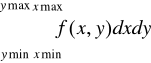
q = dblquad(fun,xmin,xmax,ymin,ymax)

q = dblquad(fun,xmin,xmax,ymin,ymax,tol)

Przykład

Oblicz następującą całkę

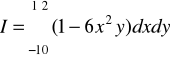
Odpowidż:

Całkowanie potrójne

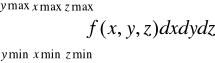
triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax)

triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol)

Q = triplequad(inline('y*sin(x)+z*cos(x)'),0,pi,0,1,-1,1)

Q = triplequad(@integrnd,0,pi,0,1,-1,1)

integrnd.m jest M-plikiem

function f = integrnd(x,y,z);

f = y*sin(x)+z*cos(x);

Z = trapz(Y)

Z = trapz(X,Y)

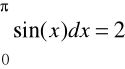
X = 0:pi/100:pi;

Y = sin(X);

Z = trapz(X,Y)

Z = pi/100*trapz(Y)

Całkowanie analityczne — Symbolic Math Toolbox

Przykład całkowania analitycznego z użyciem Symbolic Math Toolbox

(syms arg1 arg2)

syms x

y=int(1./(1+x.^2)) %calka nieoznaczona

Rezultat

y =

atan(x)

y=int(1./(1+x.^2),0,1) %calka oznaczona, granice x [0,1]

y =

1/4*pi

Zadania

Obliczyć

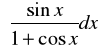
Odpowiedż

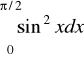
Odpowiedż

Zadania

1. Przeanalizować i przetestować program całkowania funkcji za pomocą prostych kwadratur Newtona-Cotesa (KNC) (Przykład 2).

2. Przeanalizować i przetestować program całkowania funkcji za pomocą złożonych kwadratur Newtona-Cotesa (KNC) (Przykład 5).

3. Przeanalizować i przetestować program całkowania funkcji za pomocą adaptacyjnej złożonej kwadratury Simpsona (KS) (Przykład 6).

4. Przeanalizować i przetestować program całkowania funkcji za pomocą prostych i złożonych kwadratur Gaussa-Legendre'a (KGL) (Przykład 9).

5. Przeanalizować i przetestować program całkowania funkcji za pomocą kwadratur Romberga (KR) (przykład 10).

6. Korzystająć ze wzoru trapezow i Simpsona obliczyć wartość całki:

.

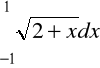
Wartość dokładna

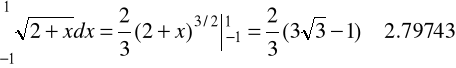
Zwiększyć dokładność, dzieląc przedział całkowania
na podprzedziały.

Programy dla przykładów

%%%%%%%%%%%%%%%%

% PRZYKЈAD 2 %

%%%%%%%%%%%%%%%%

clear all

close all

clc

kolory='ymgbrk';

% CAЈKOWANIE FUNKCJI ZA POMOCҐ PROSTYCH KWADRATUR NEWTONA-COTESA (KNC)

%===============================================================================

% Definicje caіkowanych funkcji (f1, f2, f3 i f4) jako funkcji anonimowych

%-------------------------------------------------------------------------

f1=@(x) x.*exp(x);

f2=@(x) (1-x.*x).^(0.5);

f3=@(x) exp(-abs(x));

f4=@(x) 1./(1+25*x.*x);

% Dokіadne wartoњci caіek funkcji f1, f2, f3 i f4, wyznaczone analitycznie

%-------------------------------------------------------------------------

I1=2/exp(1);

I2=pi/2;

I3=2-2/exp(1);

I4=0.4*atan(5);

a=-1;

b=1;

x=linspace(a,b,1000);

% Parametry rysunkуw

%-------------------

figsize=get(0,'ScreenSize'); % identyfikacja wielkoњci ekranu

figx=figsize(3)/2-10; if figx>630, figx=630;end % szerokoњж rysunkуw

figy=figsize(4)/2-100; if figy>412, figy=412;end % wysokoњж rysunkуw

figpos=[5 5 figx figy

figx+15 5 figx figy

5 100+figy figx figy

figx+15 100+figy figx figy]; % poіoїenia rysunkуw

% Prezentacja wykresуw funkcji f1, f2, f3 i f4

%---------------------------------------------

f=figure(1);

set(f,'Pos',figpos(1,:));

hold off

plot(x,f1(x))

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_1\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_1\rm(\itx\rm)'])

grid on

zoom on

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

f=figure(2);

set(f,'Pos',figpos(2,:));

hold off

plot(x,f2(x))

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_2\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_2\rm(\itx\rm)'])

grid on

zoom on

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

f=figure(3);

hold off

set(f,'Pos',figpos(3,:));

plot(x,f3(x))

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_3\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_3\rm(\itx\rm)'])

grid on

zoom on

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

f=figure(4);

set(f,'Pos',figpos(4,:));

hold off

plot(x,f4(x))

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_4\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_4\rm(\itx\rm)'])

grid on

zoom on

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

% Definicja macierzy wspуіczynnikуw prostej KNC

%----------------------------------------------

ln=[1,1,0,0,0,0,0;

1,4,1,0,0,0,0;

1,3,3,1,0,0,0;

7,32,12,32,7,0,0;

19,75,50,50,75,19,0;

41,216,27,272,27,216,41];

% Wyznaczenie wartoњci prostej KNC dla funkcji f1.

% Ilustracja procesu obliczeniowego, polegaj№ca na prezentacji

% wielomianu interpolacyjnego, na podstawie ktуrego jest ona wyznaczana

%----------------------------------------------------------------------

for N=1:6

wezly=linspace(a,b,N+1)'; % wyznaczenie wкzіуw kwadratury

y1=f1(wezly);

figure(1)

hold off

plot(x,f1(x))

hold on

plot(wezly,y1,['o' kolory(N)],'MarkerFaceColor',kolory(N),'MarkerSize',8)

wsp=polyfit(wezly,y1,N); % wyznaczenie wielomianu interpolacyjnego

w1=polyval(wsp,x);

h=plot(x,w1,[':' kolory(N)]);

set(h,'LineWidth',3);

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_1\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_1\rm(\itx\rm) i jej interpolacja wielomianem ',...

'Lagrange''a ',num2str(N),'-go stopnia'])

grid on

zoom on

mn=sum(ln(N,:)); % mnoїnik prostej KNC wg Tablicy 7.1

KW1(N)=(ln(N,1:N+1)*f1(wezly))*(b-a)/mn; % wartoњж prostej KNC wg wzoru (7.6)

deltaI(1,N)=(KW1(N)-I1)/I1*100; % wzglкdny bі№d prostej KNC w %

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

end

% Wyznaczenie wartoњci prostych KNC dla funkcji f2, f3 i f4.

% Ilustracja procesu obliczeniowego, polegaj№ca na prezentacji

% wielomianуw interpolacyjnych, na podstawie ktуrych s№ one wyznaczane.

%----------------------------------------------------------------------

for N=1:6

wezly=linspace(a,b,N+1);

y2=f2(wezly);

figure(2)

hold off

plot(x,f2(x))

hold on

plot(wezly,y2,['o' kolory(N)],'MarkerFaceColor',kolory(N),'MarkerSize',8)

wsp=polyfit(wezly,y2,N);

w2=polyval(wsp,x);

h=plot(x,w2,[':' kolory(N)]);

set(h,'LineWidth',3);

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_2\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_2\rm(\itx\rm) i jej interpolacja wielomianem ',...

'Lagrange''a ',num2str(N),'-go stopnia'])

mn=sum(ln(N,:));

KW2(N)=sum(ln(N,1:N+1).*f2(wezly))*(b-a)/mn;

deltaI(2,N)=(KW2(N)-I2)/I2*100;

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

end

for N=1:6

wezly=linspace(a,b,N+1);

y3=f3(wezly);

figure(3)

hold off

plot(x,f3(x))

hold on

plot(wezly,y3,['o' kolory(N)],'MarkerFaceColor',kolory(N),'MarkerSize',8)

wsp=polyfit(wezly,y3,N);

w3=polyval(wsp,x);

h=plot(x,w3,[':' kolory(N)]);

set(h,'LineWidth',3);

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_3\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_3\rm(\itx\rm) i jej interpolacja wielomianem ',...

'Lagrange''a ',num2str(N),'-go stopnia'])

mn=sum(ln(N,:));

KW3(N)=sum(ln(N,1:N+1).*f3(wezly))*(b-a)/mn;

deltaI(3,N)=(KW3(N)-I3)/I3*100;

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

end

for N=1:6

wezly=linspace(a,b,N+1);

y4=f4(wezly);

figure(4)

hold off

plot(x,f4(x))

hold on

plot(wezly,y4,['o' kolory(N)],'MarkerFaceColor',kolory(N),'MarkerSize',8)

wsp=polyfit(wezly,y4,N);

w4=polyval(wsp,x);

h=plot(x,w4,[':' kolory(N)]);

set(h,'LineWidth',3);

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=ylabel('\itf_4\rm(\itx\rm) ');

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Funkcja \itf_4\rm(\itx\rm) i jej interpolacja wielomianem ',...

'Lagrange''a ',num2str(N),'-go stopnia'])

mn=sum(ln(N,:));

KW4(N)=sum(ln(N,1:N+1).*f4(wezly))*(b-a)/mn;

deltaI(4,N)=(KW4(N)-I4)/I4*100;

fprintf('\nAby kontynuowaж, naciњnij klawisz\n')

pause

end

% Drukowanie wynikуw przedstawionych w Tablicy 7.2

fprintf(['\nBікdy wzglкdne prostych kwadratur Newtona-Cotesa dla funkcji ',...

'testowych\n'])

fprintf([' N=1 N=2 N=3 N=4 ',...

'N=5 N=6\n'])

fprintf('f1 %11.3e %11.3e %11.3e %11.3e %11.3e %11.3e\n',deltaI(1,1:6))

fprintf('f2 %11.3e %11.3e %11.3e %11.3e %11.3e %11.3e\n',deltaI(2,1:6))

fprintf('f3 %11.3e %11.3e %11.3e %11.3e %11.3e %11.3e\n',deltaI(3,1:6))

fprintf('f4 %11.3e %11.3e %11.3e %11.3e %11.3e %11.3e\n',deltaI(4,1:6))

%%%%%%%%%%%%%%%%

% PRZYKЈAD 5 %

%%%%%%%%%%%%%%%%

clear all

close all

clc

kolory='ymgbrk';

% CAЈKOWANIE FUNKCJI ZA POMOCҐ ZЈOЇONYCH KWADRATUR NEWTONA-COTESA (KNC)

%===============================================================================

% Definicje caіkowanych funkcji (f1, f2, f3 i f4) jako funkcji anonimowych

%-------------------------------------------------------------------------

f1=@(x) x.*exp(x);

f2=@(x) (1-x.*x).^(0.5);

f3=@(x) exp(-abs(x));

f4=@(x) 1./(1+25*x.*x);

% Dokіadne wartoњci caіek funkcji f1, f2, f3 i f4, wyznaczone analitycznie

%-------------------------------------------------------------------------

I1=2/exp(1);

I2=pi/2;

I3=2-2/exp(1);

I4=0.4*atan(5);

a=-1;

b=1;

x=linspace(a,b,1000);

% Definicja macierzy wspуіczynnikуw prostych KNC

%-----------------------------------------------

ln=[1,1,0,0,0,0,0;

1,4,1,0,0,0,0;

1,3,3,1,0,0,0;

7,32,12,32,7,0,0;

19,75,50,50,75,19,0;

41,216,27,272,27,216,41];

% Parametry rysunkуw

%-------------------

figsize=get(0,'ScreenSize'); % identyfikacja wielkoњci ekranu

figx=figsize(3)/2-10; if figx>630, figx=630;end % szerokoњж rysunkуw

figy=figsize(4)/2-100; if figy>412, figy=412;end % wysokoњж rysunkуw

figpos=[5 100+figy figx figy

figx+15 100+figy figx figy

5 5 figx figy

figx+15 5 figx figy]; % poіoїenia rysunkуw

figaxis=[1 100 1e-15 1;1 100 3e-4 1;1 100 1e-15 1;1 100 2e-8 1];

for i=1:4 % realizacja obliczeс kolejno dla f1, f2, f3 i f4

f=figure(i);

set(f,'Position',figpos(i,:));

hold off

for N=1:6

ind=0;

mn=sum(ln(N,:));

M=1; % inicjacja obliczeс przy uїyciu prostej KNC

st=(b-a)/M;

while N*M+1<=100 % graniczna liczba wкzіуw = 100

ind=ind+1; % indeks kolejnej kwadratury, niezbкdny do zapisywania wynikуw

ab=linspace(a,b,M+1);

Nw(ind)=N*M+1;

eval(['KW',num2str(i),'(N,ind)=0;']);

for pp=1:M % wyznaczanie prostych KNC dla kolejnych podprzedziaіуw

wezly=linspace(ab(pp),ab(pp+1),N+1);

eval(['KW',num2str(i),'(N,ind)=KW',num2str(i),'(N,ind)+sum(ln(N,1:',...

'N+1).*f',num2str(i),'(wezly))*(ab(pp+1)-ab(pp))/mn;']);

% sumowanie prostych KNC

end

eval(['bladKW',num2str(i),'(N,ind)=abs(I',num2str(i),'-KW',num2str(i),...

'(N,ind))/I',num2str(i),';']); % wyznaczanie bікdуw kwadratury

M=M*2; % powiкkszanie liczby podprzedziaіуw

end

eval(['h=loglog(Nw,bladKW',num2str(i),'(N,:),[''-'' kolory(N)]);']);

set(h,'LineWidth',2);

hold on

end

legend('N=1','N=2','N=3','N=4','N=5','N=6','Location','SouthWest')

axis(figaxis(i,:));

h=xlabel('\itN_w');

set(h,'FontName','Times','FontSize',12);

eval(['h=ylabel(''\mid\delta[\itI\rm(\itf_',num2str(i),'\rm)]\mid'');']);

set(h,'Rotation',0,'FontName','Times','FontSize',12);

title(['Zaleїnoњж bікdu wzglкdnego od liczby wкzіуw'])

pause(0.1)

end

%%%%%%%%%%%%%%%%

% PRZYKЈAD 6 %

%%%%%%%%%%%%%%%%

clear all

close all

clc

% CAЈKOWANIE FUNKCJI ZA POMOCҐ ADAPTACYJNEJ ZЈOЇONEJ KWADRATURY SIMPSONA (KS)

%===============================================================================

% Definicje caіkowanych funkcji (f1, f2, f3 i f4) jako funkcji anonimowych

%-------------------------------------------------------------------------

f1=@(x) x.*exp(x);

f2=@(x) (1-x.*x).^(0.5);

f3=@(x) exp(-abs(x));

f4=@(x) 1./(1+25*x.*x);

% Dokіadne wartoњci caіek funkcji f1, f2, f3 i f4, wyznaczone analitycznie

%-------------------------------------------------------------------------

I1=2/exp(1);

I2=pi/2;

I3=2-2/exp(1);

I4=0.4*atan(5);

% Wyznaczanie wartoњci caіek za pomoc№ zіoїonej KS i prezentacja wynikуw

% ----------------------------------------------------------------------

a=-1;

b=1;

x=linspace(a,b,1000);

% Parametry rysunkуw

%-------------------

figsize=get(0,'ScreenSize'); % identyfikacja wielkoњci ekranu

figx=figsize(3)/2-10; if figx>630, figx=630;end % szerokoњж rysunkуw

figy=figsize(4)/2-100; if figy>412, figy=412;end % wysokoњж rysunkуw

figpos=[5 100+figy figx figy

figx+15 100+figy figx figy

5 5 figx figy

figx+15 5 figx figy]; % poіoїenia rysunkуw

figaxis=[-1 1 -1 3;-1 1 0 1;-1 1 0.3 1.1;-1 1 0 1];

for i=1:4

f=figure(i);

set(f,'Position',figpos(i,:));

hold off

eval(['[I,w]=simpson(f',num2str(i),',-1,1,1e-4);']); %odwoіanie do

% zdefiniowanej niїej funkcji "simpson"

eval(['bladKW=(I-I',num2str(i),')/I',num2str(i),';']);

eval(['h=plot(w,f',num2str(i),'(w),''.b'');']);

axis(figaxis(i,:));

h=xlabel('\itx');

set(h,'FontName','Times','FontSize',12);

h=title(['Rozkіad \itN_w=\rm ',num2str(length(w)),' wкzіуw dla \itf_',...

num2str(i)]);

fprintf('Bі№d bezwzglкdny caіkowania funkcji f%1i =%10.2e (Nw=%2i)\n',i,...

bladKW,length(w));

set(h,'FontSize',10);

pause(0.1)

end

%%%%%%%%%%%%%%%%

% PRZYKЈAD 9 %

%%%%%%%%%%%%%%%%

clear all

close all

clc

kolory='ymgbrk';

% CAЈKOWANIE FUNKCJI ZA POMOCҐ PROSTYCH I ZЈOЇONYCH

% KWADRATUR GAUSSA-LEGENDRE'A (KGL)

%===============================================================================

% Definicje caіkowanych funkcji (f1, f2, f3 i f4) jako funkcji anonimowych

%-------------------------------------------------------------------------

f1=@(x) x.*exp(x);

f2=@(x) (1-x.*x).^(0.5);

f3=@(x) exp(-abs(x));

f4=@(x) 1./(1+25*x.*x);

% Dokіadne wartoњci caіek funkcji f1, f2, f3 i f4, wyznaczone analitycznie

%-------------------------------------------------------------------------

I1=2/exp(1);

I2=pi/2;

I3=2-2/exp(1);

I4=0.4*atan(5);

% Wspуіczynniki wielomianуw Legendre'a stopnia od 0 do 7

%-------------------------------------------------------

Lcoefs=[[0 0 0 0 0 0 0 1]

[0 0 0 0 0 0 1 0]

[0 0 0 0 0 3 0 -1]/2

[0 0 0 0 5 0 -3 0]/2

[0 0 0 35 0 -30 0 3]/8

[0 0 63 0 -70 0 15 0]/8

[0 231 0 -315 0 105 0 -5]/16

[429 0 -693 0 315 0 -35 0]/16];

% Wyznaczanie prostej kwadratury KGL kolejno dla funkcji f1, f2, f3 i f4

%-----------------------------------------------------------------------

for i=1:4

for N=1:6

aN1=Lcoefs(N+2,7-N); % wspуіczynnik a(N+1) we wzorze (7-17)

aN =Lcoefs(N+1,8-N); % wspуіczynnik a(N) we wzorze (7-17)

normN=2/(2*N+1); % norma wielomianu Legendre'a stopnia N

wezly=roots(Lcoefs(N+2,7-N:8)); % pierwiastki wielomianu Legendre'a

Lprim=polyder(Lcoefs(N+2,7-N:8)); % wspуіczynniki pochodnej

% wielomianu Legendre'a

An=aN1/aN*normN./polyval(Lprim,wezly)./polyval(Lcoefs(N+1,8-N:8),wezly);

% wzуr (7-17)

eval(['I(i,N)=sum(An.*f',num2str(i),'(wezly));']); % wartoњж prostej KGL

eval(['deltaI(i,N)=abs((I',num2str(i),'-I(i,N))/I',num2str(i),')*100;']);

% wzglкdny bі№d prostej KGL

pause(0.1)

end

end

% Drukowanie wynikуw przedstawionych w Tablicy 7.3

%-------------------------------------------------

fprintf(['\nBікdy wzglкdne (%%) caіkowania za pomoc№ kwadratur ',...

'Gaussa-Legendre''a\n'])

fprintf(' N=1 N=2 N=3 N=4 N=5 N=6\n')

fprintf('f1 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',deltaI(1,1:6))

fprintf('f2 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',deltaI(2,1:6))

fprintf('f3 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',deltaI(3,1:6))

fprintf('f4 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',deltaI(4,1:6))

a=-1;

b=1;

% Wyznaczanie zіoїonej kwadratury KGL kolejno dla funkcji f1, f2, f3 i f4

%------------------------------------------------------------------------

% Parametry rysunkуw

%-------------------

figsize=get(0,'ScreenSize'); % identyfikacja wielkoњci ekranu

figx=figsize(3)/2-10; if figx>630, figx=630;end % szerokoњж rysunkуw

figy=figsize(4)/2-100; if figy>412, figy=412;end % wysokoњж rysunkуw

figpos=[5 100+figy figx figy

figx+15 100+figy figx figy

5 5 figx figy

figx+15 5 figx figy]; % poіoїenia rysunkуw

figaxis=[1 100 1e-15 1;1 100 1e-5 1e-1;1 100 1e-15 1;1 100 1e-15 1];

for i=1:4

f=figure(i);

set(f,'Position',figpos(i,:));

hold off

for N=1:6

ind=0;

aN1=Lcoefs(N+2,7-N);

aN =Lcoefs(N+1,8-N);

normN=2/(2*N+1);

wezly=roots(Lcoefs(N+2,7-N:8));

Lprim=polyder(Lcoefs(N+2,7-N:8));

An=aN1/aN*normN./polyval(Lprim,wezly)./polyval(Lcoefs(N+1,8-N:8),wezly);

M=1; % inicjacja obliczeс przy uїyciu prostej KGL

while N*M+1<=100 % ograniczenie liczby wкzіуw do 100

ind=ind+1; % indeks kolejnej kwadratury niezbкdny do zapisywania wynikуw

ab=linspace(a,b,M+1);

Nw(ind)=N*M+1;

eval(['KW',num2str(i),'(N,ind)=0;']);

for pp=1:M % wyznaczenie prostych KGL dla kaїdego podprzedziaіu

% i ich sumowanie

wezly1=(wezly-((ab(pp)+ab(pp+1))/(ab(pp)-ab(pp+1))))*...

(ab(pp+1)-ab(pp))/2;

eval(['KW',num2str(i),'(N,ind)=KW',num2str(i),'(N,ind)+sum(An.*f',...

num2str(i),'(wezly1))*(ab(pp+1)-ab(pp))/2;']);

end

eval(['bladKW',num2str(i),'(N,ind)=abs(I',num2str(i),'-KW',num2str(i),...

'(N,ind))/I',num2str(i),';']); % wzglкdny bі№d zіoїonej KGL

M=M*2; % powiкkszanie liczby podprzedziaіуw

end

eval(['h=loglog(Nw,bladKW',num2str(i),'(N,:),[''-'' kolory(N)]);']);

set(h,'LineWidth',2);

title('Zaleїnoњж wzglкdnego bікdu caіkowania od liczby wкzіуw','FontSize',8)

hold on

pause(0.1)

end

legend('N=1','N=2','N=3','N=4','N=5','N=6','Location','SouthWest')

axis(figaxis(i,:));

h=xlabel('\itN_w');

set(h,'FontName','Times','FontSize',12);

eval(['h=ylabel(''\mid\delta[\itI\rm(\itf_',num2str(i),'\rm)]\mid'');']);

set(h,'Rotation',0,'FontName','Times','FontSize',12);

pause(0.1)

end

% Wyznaczenie wartoњci caіki I2 za pomoc№ kwadratury Gaussa-Czebyszewa

%---------------------------------------------------------------------

f2n=@(x) (1-x.*x); % modyfikacja caіkowanej funkcji f2 po usuniкciu funkcji wagi

wezly=[-1/sqrt(2);1/sqrt(2)];

An=[pi/2;pi/2];

Igc2=sum(An.*f2n(wezly));

fprintf(['\nUWAGA:\nBі№d kwadratury Gaussa-Czebyszewa opartej na dwуch ',...

'wкzіach \ndla funkcji f2 wynosi %10.2e\n'],abs((Igc2-I2)/I2));

%%%%%%%%%%%%%%%%%

% PRZYKЈAD 10 %

%%%%%%%%%%%%%%%%%

clear all

close all

clc

% CAЈKOWANIE FUNKCJI ZA POMOCҐ KWADRATUR ROMBERGA (KR)

%===============================================================================

f=@(x) sin(pi*x); % caіkowana funkcja

a=0; b=1; % przedziaі caіkowania

I=2/pi; % dokіadna wartoњж caіki

% Wyznaczanie KR (zіoїonej kwadratury trapezуw) dla 1, …, 128 podprzedziaіуw

%----------------------------------------------------------------------------

for w=1:10

N=2^(w-1); % liczba wкzіуw

wezly=linspace(a,b,N+1);

H=(b-a)/N;

T(w,1)=H/2*(f(a)+2*sum(f(wezly(2:N)))+f(b));

B(w,1)=abs((T(w)-I)/I);

end

for k=1:6 % k - krotnoњж ekstrapolacji

for w=1:9

T(w,k+1)=(4^k*T(w+1,k)-T(w,k))/(4^k-1); % KR dla N wкzіуw

B(w,k+1)=(T(w,k+1)-I)/I; % bі№d wzglкdny KR

end

end

% Drukowanie wynikуw przedstawionych w Tablicy 7.4

%-------------------------------------------------

fprintf('\nWzglкdne bікdy kwadratur Romberga')

fprintf(['\n N k=0 k=1 k=2 k=3 k=4 ',...

'k=5 k=6\n'])

fprintf(' 1 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',B(1,1:7))

fprintf(' 2 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',B(2,1:7))

fprintf(' 4 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',B(3,1:7))

fprintf(' 8 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',B(4,1:7))

fprintf('16 %10.2e %10.2e %10.2e %10.2e %10.2e %10.2e\n',B(5,1:6))

fprintf('32 %10.2e %10.2e %10.2e %10.2e %10.2e\n',B(6,1:5))

fprintf('64 %10.2e %10.2e %10.2e %10.2e\n',B(7,1:4))

fprintf('128 %10.2e %10.2e %10.2e\n',B(8,1:3))

Dodatek

Wzór trapezów na przedziale
:

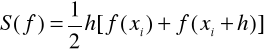
Wzór Simpsona (parabol) na przedziale
:

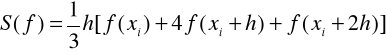
4

---