Spis treści

	Wprowadzenie	2
1.	Modele szeregów czasowych z trendem	6
	1.1. Wybór postaci analitycznej modelu	6
	1.2. Arkusz wyników dodatku programowego „REGRESJA”	12
2.	Modele szeregów czasowych ze stałym poziomem zmiennej prognozowanej	22
	2.1. Metoda naiwna	23
	2.2. Modele średniej ruchomej	24
	2.3. Prosty model wygładzania wykładniczego	25
3.	Prognozy na podstawie modelu wyrównywania wykładniczego	26
	3.1. Model liniowy Browna	26
	3.2. Model nieliniowy z dwoma parametrami	27
	3.3. Model liniowy Holta	28
	3.4. Model Wintersa	29
4.	Analiza wahań okresowych	30
	4.1. Metoda wskaźników	30
	4.2. Metoda L. R. Kleina	31
	4.3. Metoda trendów jednoimiennych	31
	Literatura	32

Wprowadzenie

Dane otrzymane w wyniku obserwacji zjawiska w jednakowo oddalonych od siebie momentach czasu lub w kolejnych, równych sobie, przedziałach czasu tworzą tzw. szereg czasowy. Zmiany zjawiska w czasie mogą podlegać pewnym prawidłowościom, których wykrycie i opis jest przedmiotem analizy szeregu czasowego. Najczęściej stwierdza się występowanie w szeregu czasowym następujących składników:

• tendencja rozwojowa (trend)

• wahania okresowe

• wahania cykliczne

• wahania przypadkowe.

Tendencja rozwojowa jest własnością szeregu czasowego ujawniającą się poprzez systematyczne, jednokierunkowe zmiany (wzrost lub spadek) poziomu badanego zjawiska zachodzące w długim okresie. Charakter tych zmian (systematyczność i długotrwałość) pozwala przypuszczać, że przyczyną występowania określonego trendu w rozwoju zjawiska jest stałe oddziaływanie na zjawisko pewnego splotu czynników określanych mianem przyczyn głównych.

Wahania okresowe są to rytmiczne wahania o określonym cyklu (okresie przebiegu). Najczęściej obserwuje się wahania o cyklu rocznym, przy czym podokresami cyklu w takim przypadku mogą być półrocza, kwartały, miesiące, a nawet dni.

Wahania koniunkturalne to systemowe, falowe wahania rozwoju gospodarki obserwowane w dłuższych od roku okresach. Analiza tego rodzaju wahań wymaga wieloletnich obserwacji.

Wahania przypadkowe wyrażają wpływ na zmienną y czynników losowych oraz błędów wynikających ze specyfikacji modelu.

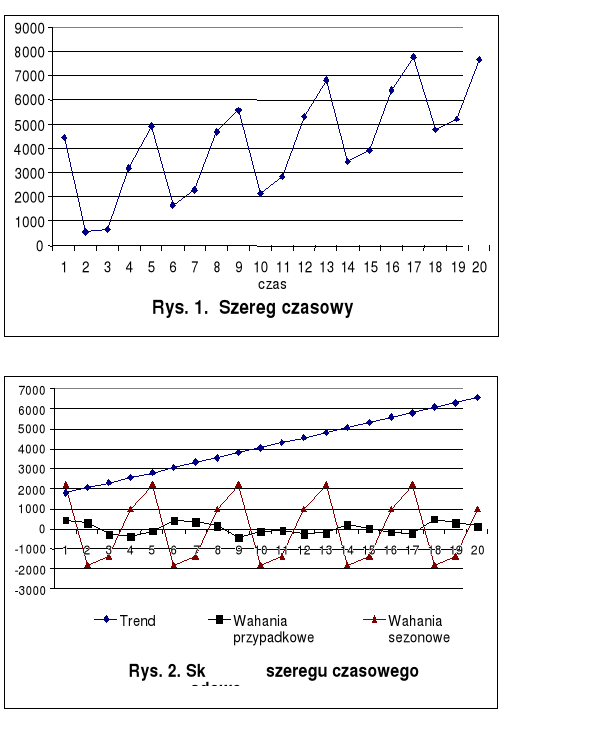
Identyfikację poszczególnych składowych szeregu czasowego konkretnej zmiennej umożliwia w wielu przypadkach ocena wzrokowa sporządzonego wykresu danych. Wykres przykładowego szeregu czasowego, z różnymi rodzajami składowych zamieszczono na rys. 1 i 2.

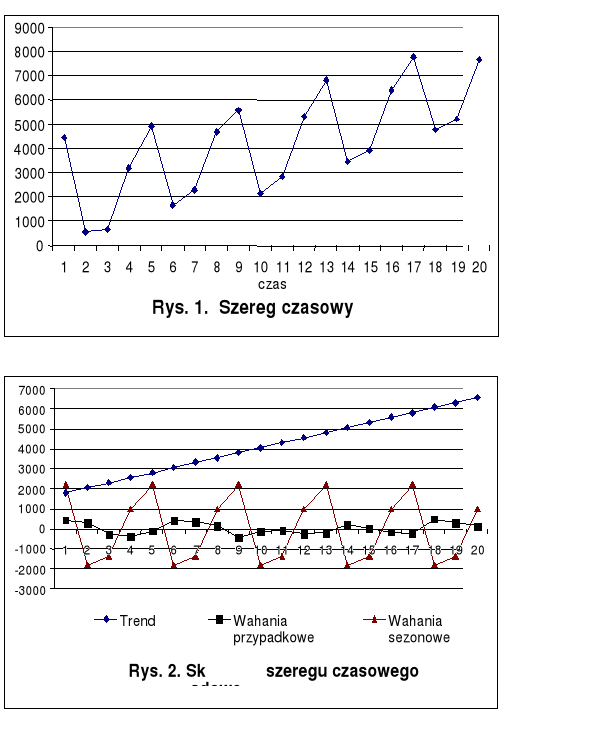
Prawidłowości rozwoju zjawiska wykryte w szeregach czasowych opiszemy w postaci modelu opisującego zależność poziomu zjawiska od czasu, czyli w postaci funkcji:

y_t = f(t) + g(t) + ε_t (1)

lub

y_t = const + g(t) + ε_t (2)

gdzie:

f(t) - funkcja czasu, charakteryzująca tendencje rozwojową szeregu, czyli funkcja trendu,

g(t) - funkcja czasu, charakteryzująca wahania sezonowe

ε_t - zmienna losowa, charakteryzująca efekty oddziaływania wahań przypadkowych

const - stały, średni poziom zmiennej

Nie oznacza to, że czas jest przyczyną zmian zachodzących w poziomie zjawiska, lecz że zmiany czasu są wyrazem zmiany warunków jakie towarzyszą danemu zjawisku ( K. Zając [7] ).

Celem analizy szeregów czasowych jest:

• oszacowanie parametrów wybranego modelu kształtowania się zmiennej i ocena dokładności dopasowania modelu do danych empirycznych ( ten etap badania szeregu czasowego dotyczy przeszłości i często jest nazywany diagnozowaniem przeszłości)

• wykorzystanie oszacowanego modelu do sporządzenia prognozy kształtowania się analizowanego zjawiska w przyszłych okresach.

Prognozowanie na podstawie modeli typu (1) i (2) polega na prostej ekstrapolacji funkcji trendu (i ewentualnie funkcji g(t)) przez podstawienie do modelu w miejsce zmiennej czasowej numeru momentu/okresu - T, na który wyznacza się prognozę:

Jednakże tego rodzaju ekstrapolacja może być stosowana do sporządzania prognoz jedynie w tym przypadku, jeżeli nie ma wyraźnych okoliczności przemawiających przeciw zasadzie dynamicznego „status quo" ( A. Zeliaś [8] ) Zasada dynamicznego „status quo" oznacza, że postać analityczna funkcji trendu f(t) i wartości jej parametrów w okresie T, na który dokonuje się prognozy, nie mogą ulec istotnej zmianie w porównaniu z okresem, którego dotyczyły informacje liczbowe służące za podstawę do szacowania modelu. Natomiast wszędzie tam, gdzie następuje istotna zmiana dotychczasowego regularnego przebiegu zjawiska w czasie, metoda prostej ekstrapolacji zawodzi, prowadząc na ogół do dużych błędów wnioskowania w przyszłość.

W takich przypadkach bardziej wskazane jest skorzystanie z modelu przyczynowo-skutkowego, który umożliwia ocenę siły wpływu poszczególnych zmiennych objaśniających na zmienną prognozowaną.

1. Modele szeregów czasowych z trendem

Model szeregu czasowego, w którym występuje tendencja rozwojowa oraz wahania przypadkowe , a rolę zmiennej objaśniającej odgrywa zmienna czasowa nazywamy modelem tendencji rozwojowej. Zapis modelu jest następujący:

y_t = f(t) + ε_t dla t = 1, 2, .... ,n

gdzie:

f(t) - funkcja czasu, charakteryzująca tendencję rozwojową szeregu, nazywana funkcją trendu,

ε_t - zmienna losowa, charakteryzująca efekty oddziaływania wahań przypadkowych.

Zadanie wyznaczenia funkcji f(t) jest nazywane wygładzaniem (wyrównywaniem) szeregu czasowego. Najczęściej stosowane metody wygładzania to:

• Metody analityczne, przy pomocy których określamy postać analityczną funkcji trendu i jej parametry;

• Metody adaptacyjne, w których nie zakłada się stałej postaci analitycznej trendu, lecz przeciwnie, zakłada się, że dla każdego okresu ocenę poziomu trendu buduje się jako pewną przeciętną z tego rodzaju ocen dokonanych w poprzednich okresach.

1.1 Wybór postaci analitycznej funkcji trendu

Podstawą metody analitycznej wygładzania szeregu czasowego jest wyznaczenie postaci funkcji trendu i jej parametrów.

W sformułowaniu hipotezy dotyczącej postaci analitycznej funkcji trendu pomoże nam przede wszystkim praktyczna znajomość prawidłowości kształtowania się badanej zmiennej w przeszłości, dotycząca np. założeń o stałych przyrostach absolutnych bądź względnych w czasie. Pomocą jest również ocena wzrokowa wykresu danych, którą w przypadku analizy szeregu czasowego w arkuszu kalkulacyjnym Excel znakomicie ułatwia możliwość automatycznego dodania linii trendu do serii danych na wykresie.

Analizę danych rozpoczynamy więc od sporządzenia wykresu (najczęściej liniowego). Następnie wykonujemy następujące kroki:

• Uaktywniamy wykres

• Zaznaczamy serie danych do której chcemy dodać linię trendu lub średnią ruchomą

• Z menu Wykres wybieramy polecenie Dodaj linię trendu.

• 
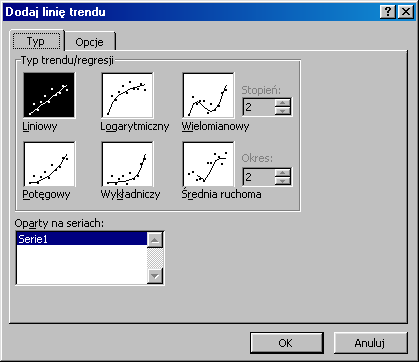
  Z okna dialogowego Dodaj linię trendu wybieramy opcję Typ (rys. 1.1), która umożliwia wybór postaci analitycznej funkcji trendu. W przypadku wielomianu należy określić stopień wielomianu, a w przypadku średniej ruchomej należy podać długość okresu w polu Okres

Rys. 1.1 Okno dialogowe Dodaj linie trendu - wybór postaci funkcji trendu

• W zakładce Opcje (rys.1.2), w pole Naprzód wpisujemy liczbę jednostek o które chcemy przedłużyć linię trendu. Wyświetl równanie na wykresie powoduje pojawienie się na wykresie równania trendu, natomiast zaznaczenie opcji Wyświetl wartości R-kwadrat na wykresie - wartości współczynnika determinacji R² (nie dotyczy to trendu wyznaczonego na podstawie średniej ruchomej).

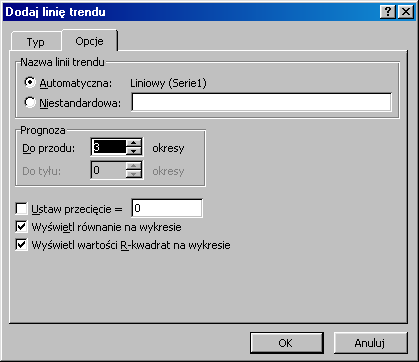
Rys.1.2. Okna dialogowe Dodaj linie trendu - zakładka Opcje

Okno dialogowe Dodaj linię trendu umożliwia nam wybranie następujących postaci trendu:

1. trend liniowy

y_t = a+bt (1.1)

Jest to najczęściej wykorzystywana w praktyce postać funkcji trendu, stosowana zawsze w przypadku, gdy można przyjąć założenie o stałych przyrostach wartości zmiennej y w jednostce czasu. Parametry funkcji zostały oszacowane metodą najmniejszych kwadratów.

2. trend logarytmiczny

y_t = a + b log t (1.2)

Ten typ trendu wybieramy gdy wzrost badanej zmiennej jest coraz wolniejszy. Po wprowadzeniu podstawienia: t^' = log t, otrzymujemy równanie liniowe:

y_t = a + b t^' ,

którego parametry zostały oszacowane metodą najmniejszych kwadratów. Jest to przykład trendu nieliniowego, ale liniowego względem parametrów.

3. trend wielomianowy (omówimy go na przykładzie funkcji kwadratowej trendu)

y_t = at² + bt + c (1.3)

Po podstawieniu: t² = x₂, t = x₁, otrzymujemy funkcję liniową dwóch zmiennych: y_t= a x₂ + b x₁ + c, której parametry zostały oszacowane metodą najmniejszych kwadratów. Jest to również przykład trendu nieliniowego, ale liniowego względem parametrów.

Uwaga

Wiadomo, że każdą funkcję ciągłą i ograniczoną można w skończonym przedziale aproksymować z dowolną dokładnością wielomianem odpowiedniego stopnia. Korzystając więc z funkcji wielomianowej trendu możemy uzyskać bardzo wysoką zgodność modelu z obserwacjami empirycznymi, dla t=1,2,..., n (czyli dla o odcinka czasu, z którego pochodzą dane empiryczne), nie mamy natomiast żadnej gwarancji, że otrzymana funkcja trendu równie dobrze opisze zmiany zmiennej y w przyszłości. W opinii wielu autorów (np. Z. Pawłowski [5] ) prócz funkcji liniowej wielomiany nie mają zbyt silnego uzasadnienia jako podstawa predykcji. Na rys. 1.3 przedstawiono wykres danych empirycznych i wartości wygładzonych przy pomocy wielomianu 5-tego stopnia, przy czym trend wielomianowy wyznaczono na podstawie 24 danych. Jak widać dopasowanie funkcji trendu jest do danych jest bardzo dobre (R² = 0,923; S_u = 8,7). Na rys. 1.4 widzimy natomiast, jak duża jest rozbieżność pomiędzy dwoma następnymi wartościami empirycznymi, a wartościami prognoz wyznaczonych na podstawie wielomianowej funkcji trendu.

Rys. 1.3. Wartości empiryczne i wygładzone na podstawie trendu wielomianowego

Rys. 1.4 Porównanie wartości prognoz wyznaczonych na podstawie trendu wielomianowego i wartości rzeczywistych dla T=25, 26.

4. trend potęgowy

y_t = a t^b (1.4)

Tę postać funkcji trendu stosuje się najczęściej w przypadku, gdy wykładnik b jest większy od zera, lecz mniejszy od jedności, wtedy funkcja (1.4) charakteryzuje się malejącym tempem wzrostu. Jest to przykład funkcji nieliniowej względem parametrów. Aby sprowadzić ją do postaci liniowej, logarytmujemy obie strony wyrażenia (1.4), a następnie można już oszacować parametry otrzymanej funkcji liniowej (1.5) metodą najmniejszych kwadratów.

lny_t = ln a + b ln t

Po podstawieniach:

z_t = ln y_t , a^' = lna, t^' = ln t

otrzymujemy funkcję liniową:

z_t = a^' + b t^' (1.5)

5. trend wykładniczy

y_t= a b^t (1.6)

lub: y_t= a e^bt (1.7)

Własnością charakterystyczną tej funkcji trendu są stałe w czasie przyrosty względne. Podobnie jak funkcję potęgową, przed estymacją parametrów a i b sprowadzamy ją do postaci liniowej za pomocą logarytmowania obu stron wyrażenia (1.6):

ln y_t = ln a + t ln b (1.8)

Jeśli przyjmiemy następujące oznaczenia:

z_t = ln y_t , a^' = ln a, b^' = ln b.

otrzymamy funkcję liniową:

z_t = a^' + b^' t,

której parametry można już oszacować metodą najmniejszych kwadratów.

Do estymacji parametrów wszystkich funkcji trendu dostępnych w oknie dialogowym Dodaj linie trendu zastosowano w arkuszu kalkulacyjnym Excel metodę najmniejszych kwadratów. W przypadku funkcji trendów liniowych względem parametrów (funkcja logarytmiczna i wielomianowa), funkcję liniową otrzymano po odpowiednim przekształceniu zmiennych niezależnych w modelu, natomiast w przypadku funkcji nieliniowych względem parametrów (funkcja potęgowa i wykładnicza), aby przejść do modelu liniowego należało przekształcić również zmienną zależną y_t .

1.2. Arkusz wyników dodatku programowego „REGRESJA”

Po wyborze postaci analitycznej funkcji trendu na podstawie oceny wzrokowej wykresów danych empirycznych i funkcji trendu, przechodzimy do drugiego etapu analizy szeregu czasowego tzn. do oszacowania parametrów strukturalnych (parametrów funkcji trendu) i stochastycznych (odchylenia standardowego składnika losowego) modelu oraz do oceny jakości otrzymanego modelu obliczając odpowiednie miary dokładności dopasowania funkcji trendu do danych empirycznych.

Do dokładnego oszacowania parametrów strukturalnych i stochastycznych modelu wykorzystamy narzędzie analizy danych: Regresja. Jeżeli w opcji Narzędzia, w głównym menu arkusza, nie znajdujemy polecenia Analiza danych należy uaktywnić zbiór procedur programu Excel pod nazwą Dodatki. W tym celu z głównego menu wybieramy opcje: Narzędzia →Dodatki. W wyświetlonym wówczas oknie dialogowym uaktywniamy dodatki: Analysis ToolPak i Analysis ToolPak - VBA, co spowoduje zwiększenie liczby dostępnych funkcji obliczeniowych (rys.1.5).

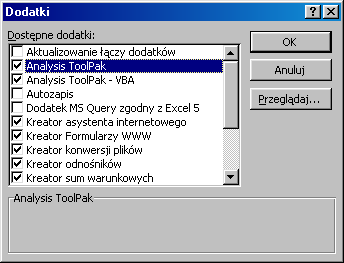
Rys. 1.5. Okno dialogowe Dodatki

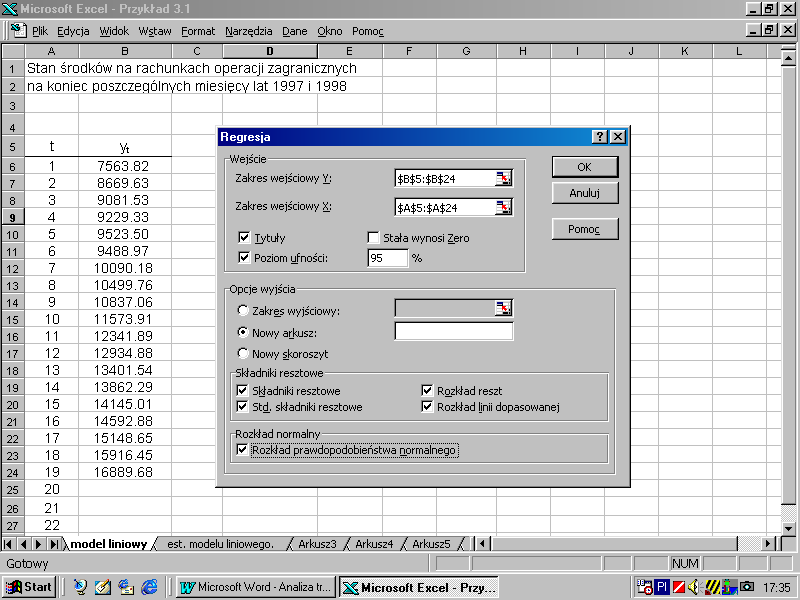
Po zainstalowaniu odpowiednich dodatków, w aktywnym oknie z wprowadzonymi danymi, z głównego menu wybieramy: Narzędzia→ Analiza danych→Regresja (rys. 3.6).

Opcja Regresja umożliwia oszacowanie parametrów modelu regresji liniowej postaci:

Y_t = α₀ + α₁X_1t +α₂ X_2t +.... +α_k X_kt + ε_t (1.9)

gdzie: X_1t, X_2t, ... X_kt - zmienne objaśniające modelu

ε_t - składnik losowy modelu

α_i - parametry strukturalne modelu

Zakres wejściowy Y obejmuje obserwacje zmiennej zależnej Y ( dla modeli trendu 1.1-1.3 jest to zmienna y_t, natomiast dla modelu potęgowego i wykładniczego jest to zmienna ln(y_t)). Natomiast Zakres wejściowy X obejmuje obserwacje zmiennych objaśniających występujących w modelu; przykładowo w modelu regresji wielorakiej (1.9) Zakres wejściowy X obejmie k kolumn obserwacji zmiennych X_1t, X_2t, ... X_kt, natomiast w przypadku trendu liniowego, którego analizę przeprowadzono w arkuszu roboczym na rys. 1.6 jest to zmienna t, której wartości w postaci kolejnych liczb naturalnych od 1-19 zaznaczono w komórkach A6:A19. Zaznaczenie opcji Stała wynosi Zero spowoduje, że wyraz wolny równania regresji wyniesie 0. Zaznaczenie pól wyboru Składniki resztowe spowoduje:

• Składniki resztowe - obliczenie wartości reszt
  ;

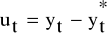
• Std. Składniki resztowe - obliczenie standaryzowanych wartości reszt

równych ilorazowi:
;

• Rozkład reszt - otrzymanie wykresu wartości reszt względem każdej zmiennej objaśniającej, w przypadku trendu liniowego jest to wykres reszt w czasie;

• Rozkład linii dopasowanej - otrzymanie wykresów wartości empirycznych i wartości teoretycznych, czyli wartości funkcji trendu;

• 
  Rozkład prawdopodobieństwa normalnego - otrzymanie wykresu krzywej częstości skumulowanych opartą na percentylach.

Rys. 1.6. Okno dialogowe Regresja

Po naciśnięciu przycisku OK w nowym arkuszu uzyskujemy podsumowanie regresji. Poszczególne tablice tego podsumowania przedstawiają tablice 1.1-1.3.

Tablica 1.1 Statystyki regresji

PODSUMOWANIE - WYJŚCIE
Statystyki regresji		uwagi
Wielokrotność R	0.9914	współczynnik korelacji wielorakiej
R kwadrat	0.9829	współczynnik determinacji
Dopasowany R kwadrat	0.9819	skorygowany współczynnik determinacji
Błąd standardowy	366.7	odchylenie standardowe reszt
Obserwacje	19	liczba obserwacji

Współczynnik determinacji jest jedną z podstawowych miar dopasowania modelu regresji liniowej do danych empirycznych. Obliczamy go ze wzoru:

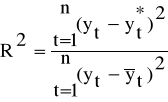
(1.10)

gdzie: n - liczebność próby (liczba okresów)

- wartość realizacji zmiennej prognozowanej w okresie t

- wartość teoretyczna wyznaczonej funkcji regresji dla t = 1,2,... ,n,

( w przypadku modeli tendencji rozwojowej są to wartości

wyznaczonej funkcji trendu)

Wartość współczynnika determinacji R2 zawiera się w przedziale <0,1> i informuje jaka część zaobserwowanej, całkowitej zmienności y_t została wyjaśniona przez model trendu.

Współczynnik korelacji wielorakiej R jest równy dodatniemu pierwiastkowi z wartości współczynnika determinacji i mierzy siłę związku liniowego zmiennej objaśnianej Y ze zbiorem zmiennych objaśniających występujących w modelu.

Ponieważ wartość współczynnika determinacji R² rośnie wraz z liczbą dodatkowych zmiennych objaśniających uwzględnionych w modelu, nie może on być używany do porównania stopnia dopasowania modeli o różnej liczbie zmiennych objaśniających. Do tego celu można wykorzystać skorygowany współczynnik determinacji
.

Dopasowany R kwadrat jest to skorygowany o liczbę zmiennych objaśniających w modelu współczynnik determinacji, który obliczamy ze wzoru:

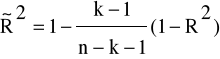
(1.11)

gdzie:

n- liczba obserwacji zmiennej objaśnianej

k- liczba zmiennych objaśniających występujących w modelu

Oba współczynniki determinacji stosujemy jedynie do modeli trendów liniowych i modeli liniowych względem parametrów . Współczynnik R² nie może być używany jako miara dopasowania modelu wykładniczego i potęgowego w postaci (1.4) i (1.6) do danych empirycznych, gdyż współczynnik ten został policzony dla modelu liniowego, w którym zmienną zależną była zmienna z_t = ln y_t. Problemowi temu poświęcimy jeszcze uwagę przy omawianiu rozwiązań konkretnych przykładów zastosowania wspomnianych funkcji trendu.

Inną , bardzo ważną miarą dopasowania funkcji trendu do danych empirycznych jest odchylenie standardowe składnika resztowego, które obliczamy ze wzoru:

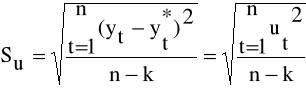
(1.12)

gdzie:

n - liczebność próby

k - liczba szacowanych parametrów

- wartość realizacji zmiennej prognozowanej w okresie t

- wartości teoretyczne, obliczone na podstawie oszacowanej funkcji

regresji

Wielkość odchylenia standardowego reszt interpretujemy jako przeciętne odchylenie zaobserwowanych wartości zmiennej yt od odpowiadających im wartości funkcji trendu.

Tablica 1.2. Analiza wariancji

ANALIZA WARIANCJI
	df	SS	MS	F	Istotność F
Regresja	1	131201713.6	131201713.6	975.691	1.86028E-16
Resztkowy	17	2285997.385	134470.4344
Razem	18	133487711

Oznaczenia:

df (degrees of freedom) - liczba stopni swobody

SS(Sum of Squares) - suma kwadratów

MS(Mean Squares) - średnie kwadraty (suma kwadratów podzielona przez liczbę stopni swobody)

Wiadomo, że jeżeli oszacujemy model regresji liniowej postaci (3.9) klasyczną metodą najmniejszych kwadratów, to zachodzi równość: suma kwadratów odchyleń zmiennej objaśnianej od jej wartości średniej (czyli zmienność zmiennej zależnej) jest sumą zmienności wyjaśnionej regresją i zmienności resztowej. Wartości te są zapisane w kolumnie trzeciej tablicy 2. Na ich podstawie została obliczona wartość statystyki F, która jest sprawdzianem następującej hipotezy:

H₀ : R=0 (lub, α_i =0, dla i=1,2,.. k)

H₁: R > 0 (lub przynajmniej jedno α_i≠0)

Zweryfikowanie tej hipotezy, o istotności współczynnika korelacji wielorakiej, pozwala na stwierdzenie, czy zbiór zmiennych objaśniających wpływa istotnie na zmienną y. Decyzję odnośnie przyjęcia bądź odrzucenia hipotezy H₀ podejmujemy na podstawie wartości prawdopodobieństwa p = P(F>F_obl). Wartość F_obl znajduje się w kolumnie o tytule F, natomiast wartość prawdopodobieństwa p znajduje się w ostatniej kolumnie tablicy 1.2 i nosi nazwę Istotność F. Jeśli prawdopodobieństwo p jest nie większe od przyjętego poziomu istotności, to sprawdzaną hipotezę odrzucamy, czyli wartość współczynnika korelacji wielorakiej jest istotnie różna od zera.

Tablica 1.3 zawiera wyniki oszacowania parametrów strukturalnych modelu i pozwala na ocenę ich istotności.

Tablica 1.3. Wyniki oszacowania parametrów strukturalnych modelu

	Współczynniki	Błąd standardowy	t Stat	Wartość-p	Dolne 95%	Górne 95%
Przecięcie	7086.043	175.125	40.46	2.416E-18	6716.56	7455.52
t	479.769	15.359	31.24	1.86E-16	447.36	512.17

Objaśnienia:

Bląd standardowy - średni błąd szacunku, miara precyzji oszacowania parametru strukturalnego modelu

T - Stat - iloraz ocen parametrów i średnich błędów szacunku

Wartość-p - wartość prawdopodobieństwa p = P(t>T-stat).

Dolne 95% - Górne 95% - końce przedziałów ufności wyznaczonych dla współczynników regresji dla współczynnika ufności 1-α = 0,95.

Istotnym punktem weryfikacji modelu jest sprawdzenie, czy uwzględnione w modelu zmienne objaśniające wpływają istotnie na kształtowanie się zmiennej objaśnianej. Sprawdzianem hipotezy zerowej

H₀: α_i =0,

wobec hipotezy alternatywnej H₁: α_i ≠0 jest statystyka t-Studenta o n-k-1 stopniach swobody równa ilorazowi oceny danego parametru i jego średniego błędu szacunku (są to wartości T - Stat podane w tablicy 2). Jeżeli wartość prawdopodobieństwa p = P(t>T-stat) jest nie większa od przyjętego poziomu istotności ( najczęściej przyjmujemy α = 0,05) to sprawdzaną hipotezę odrzucamy, czyli wartość oceny danego parametru jest istotnie różna od zera. Innymi słowy, jeżeli wszystkie wartości p w tablicy 1.2 są mniejsze od przyjętego poziomu istotności np. 0,05, to wszystkie zmienne uwzględnione w modelu są istotne.

Arkusz podsumowania opcji Regresja ułatwia również analizę reszt, której celem jest sprawdzenie wybranych założeń klasycznej metody najmniejszych kwadratów i rozstrzygnięcie dwóch podstawowych kwestii: czy postać analityczna modelu jest poprawna i czy uwzględniono w nim właściwe zmienne objaśniające. Do badania reszt możemy wykorzystać analizę graficzną na podstawie otrzymanych w arkuszu wykresów (rys 1.7, 1.8).

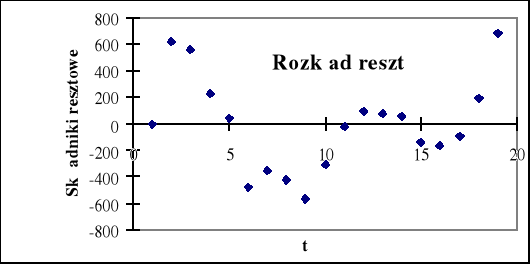
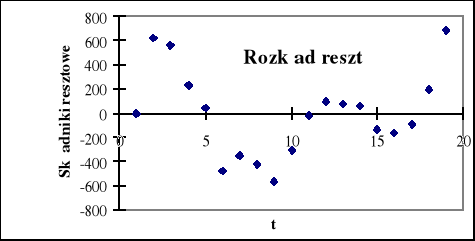
Rys. 1.7. Rozkład reszt

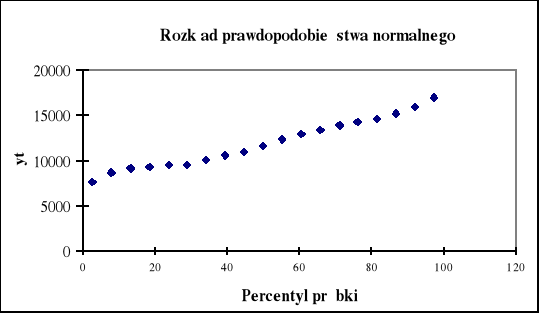
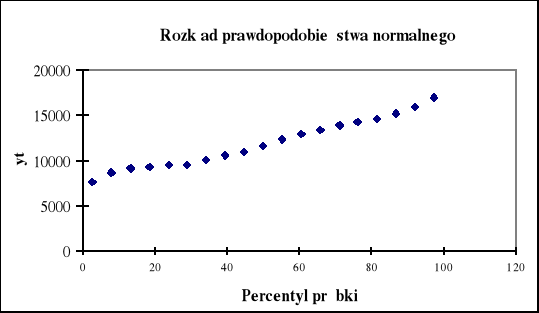
Rys. 1.8. Zgodność rozkładu reszt z rozkładem normalnym

Najprostszą charakterystyką poprawnego rozkładu reszt jest jego symetria, która oznacza równe prawdopodobieństwa występowania reszt ujemnych i dodatnich. Na rys. 1.7 liczba reszt dodatnich wynosi 9, a ujemnych -10, tak więc można przyjąć, że reszty te spełniają własność symetrii.

Kolejną własnością , którą według założeń winny spełniać reszty, jest ich losowość. Weryfikacja hipotezy o losowości ciągu reszt ma na celu ocenę trafności doboru postaci analitycznej funkcji regresji ( w przypadku modelu tendencji rozwojowej jest to wybór właściwej postaci analitycznej funkcji trendu ). Do weryfikacji hipotezy H₀ : y = f(x) wobec hipotezy alternatywnej: H₁: y ≠ f(x) służy tzw. test liczby serii.

Punktem wyjścia jest ciąg reszt uszeregowany według kolejności jednostek czasu. Dla tego uporządkowanego ciągu oblicza się liczbę serii reszt modelu - S. Serią jest każdy podciąg reszt złożony wyłącznie z elementów dodatnich lub ujemnych. Z tablic testu liczby serii dla danej liczby reszt dodatnich n₁, liczby reszt ujemnych n₂, oraz przyjętego poziomu istotności α ( tj. dla α/2 i 1-α/2) odczytuje się dwie krytyczne liczby serii: S₁ i S₂ . Jeśli:

S₁ ≤ S ≤ S₂,

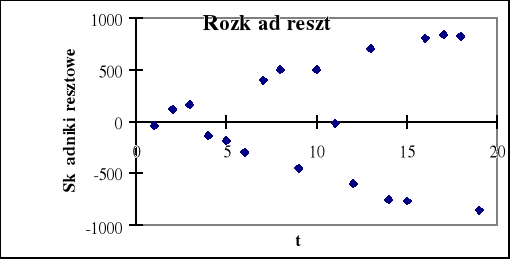
to nie ma podstaw do odrzucenia hipotezy H₀ . Oznacza to, że ciąg reszt jest losowy, wobec czego postać analityczna modelu została dobrana trafnie. Jeżeli liczba serii jest w przybliżeniu równa połowie liczby obserwacji, możemy być pewni, że reszty są losowe. W naszym przykładzie na rys. 7 widzimy 5 serii, więc bez skorzystania z tablic nie mamy pewności, jaką decyzję powinniśmy podjąć. Wykres reszt według następstwa czasowego pozwala również na ocenę jednorodności wariancji.

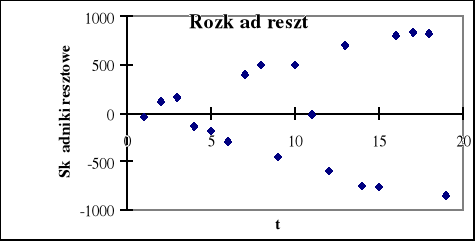
Rys. 1.9. Badanie stałości wariancji

Na rys. 1.9 wyraźnie widzimy że odchylenie standardowe reszt ( średnia odległość punktów wykresu od osi czasu) nie jest stałe w danym okresie, lecz wykazuje tendencję rosnącą, nie jest więc spełnione założenie o jednorodności wariancji.

W regresji wielorakiej zakłada się również, że wartości resztowe posiadają rozkład normalny. Wykres rozkładu prawdopodobieństwa normalnego (rys.1.8) pozwala na szybką wizualną ocenę zgodności reszt z rozkładem normalnym. Jeśli nie posiadają one rozkładu normalnego, to nastąpią odstępstwa od linii prostej. Na tym wykresie ujawnią się również obserwacje odstające (nietypowe).

2. Modele szeregów czasowych ze stałym poziomem zmiennej

prognozowanej

Gdy w szeregu czasowym występuje składowa systematyczna w postaci stałego (przeciętnego) poziomu i wahania przypadkowe, do prognozowania używa się zwykle następujących metod:

• metodę naiwną

• metody średniej ruchomej

• prosty model wygładzania wykładniczego.

Metody te umożliwiają (na ogół) konstrukcję prognoz krótkookresowych - na jeden kolejny okres, czyli na okres t = n + 1, gdzie n oznacza numer ostatniej obserwacji zmiennej prognozowanej.

Wartość prognostyczna modeli zostanie określona ex post po obliczeniu wartości bezwzględnych błędów prognoz na podstawie miary MAE (Mean Absolute Error) zadanej wzorem:

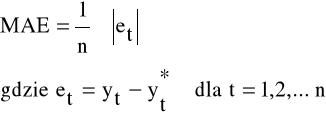
gdzie:

- wartość realizacji zmiennej prognozowanej w okresie t

- poziom prognozy odpowiadający okresowi t dla t = 1,2,... ,n

Dla zadanego szeregu czasowego prognoza zostanie wyznaczona na podstawie modelu, dla którego miara ta będzie najmniejsza. Prognozę na okres (n+1) wyznaczoną na podstawie jednej z trzech wymienionych metod, uznamy za dopuszczalną, jeżeli błąd względny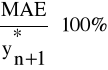
nie będzie większy niż z góry zadana wartość (najczęściej 5%-10%).

2.1 Metoda naiwna

Metodę naiwną warto stosować jedynie przy niewielkich wahaniach przypadkowych. O sile tych wahań informuje nas wielkość współczynnika zmienności badanego szeregu czasowego, który obliczamy ze wzoru:

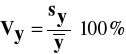
(2.1)

gdzie: s_y- odchylenie standardowe zmiennej y

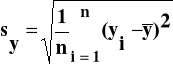
(2.2)

- wartość średnia zmiennej y

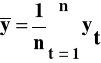
(2.3)

Współczynnik zmienności jest miarą niemianowaną, która mierzy stopień zróżnicowania obserwacji zmiennej y. Przyjmuje się, że jeżeli współczynnik zmienności przyjmuje wartości poniżej 10%, to zmienna wykazuje statystycznie nieistotne zróżnicowanie.

W modelu naiwnym wykorzy­stywanym w takich przypadkach konstruuje się prognozę zmiennej na mo­ment lub okres t na poziomie zaobserwowanej wartości tej zmiennej w mo­mencie lub okresie t - 1, czyli:

(2.4)

gdzie:

- prognoza zmiennej y wyznaczona na okres t

- wartość zmiennej y w okresie t-1.

Metoda naiwna może być wykorzystana do porównania trafności konstruowanych za jej pomocą prognoz i prognoz budowanych innymi, bardziej skomplikowanymi metodami oraz do oceny celowości stosowania tych bardziej wyrafinowanych metod prognozowania.

2.2. Modele średniej ruchomej

Modele średniej ruchomej mogą być wykorzystywane zarówno do wygładza­nia szeregu czasowego, jak i do prognozowania.

Idea wyrównywania szeregu czasowego za pomocą średnich ruchomych (tzw. metoda mechaniczna wygładzania szeregu) polega na zastąpieniu pierwotnych wartości zmiennej prognozowanej średnimi arytmetycznymi, obliczanymi sekwencyjnie dla wybranej liczby obserwacji. Wyznaczone wartości średnie przyporządkowuje się na ogół środkowym obserwacjom, na których podstawie obliczono średnie.

Modele średniej ruchomej stosuje się do prognozowania, gdy w roz­patrywanym okresie poziom wartości zmiennej prognozowanej jest prawie stały, z niewielkimi odchyleniami losowymi, a w szeregu czasowym nie występują inne składowe.

Używając modeli średniej ruchomej do prognozowania, przyjmuje się, że war­tość zmiennej prognozowanej w następnym momencie/okresie będzie równa średniej arytmetycznej z k ostatnich wartości tej zmiennej. Formuła obliczania prognozy na podstawie modelu średniej ruchomej prostej jest następująca:

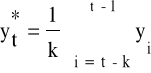
(2.5)

gdzie:
- prognoza zmiennej y wyznaczona na okres t

- wartość zmiennej y w okresie i.

Liczba wyrazów średniej ruchomej (k), czyli stała wygładzania, jest określana przez prognostę. Jej wybór może być oparty na badaniu MAE czyli błędu prognozy ex post. Spośród różnych, wstępnie przyjętych wartości stałej k jako ostateczną wartość wybiera się tę, w przypadku której wielkość tego błędu jest najmniejsza. Gdy k= 1, model sprowadza się do modelu (2.4) metody naiwnej.

2.3. Prosty model wygładzania wykładniczego

Wadą modelu średniej ruchomej jest nadawanie tych samych wag (jednostkowych) wszystkim k wartościom zmiennej prognozowanej, na których pod­stawie wyznacza się prognozę. Tymczasem słuszny wydaje się postulat, aby nowsze dane, które zawierają bar­dziej aktualne informacje o prognozowanym zjawisku, miały relatywnie większe wagi niż obserwacje starsze. Postulat ten, określany mianem postarzania informacji, spełniają modele wygładzania wykładniczego.

Istota wygładzania wykładniczego polega na tym, że szereg czasowy zmiennej prognozowanej wygładza się za pomocą średniej ruchomej ważonej, przy czym wagi są określane według prawa wykładniczego. Wygładzanie wykładnicze może być oparte na różnych modelach, w zależności od rodzaju składowych szeregu czasowego.

Prosty model wygładzania wykładniczego może być stosowany do prognozo­wania zmiennej w przypadku, gdy w szeregu czasowym występuje składowa systematyczna w postaci stałego (przeciętnego) poziomu i wahania przypadkowe. Prognozę na jego podstawie oblicza się następująco:

α - parametr wygładzania

Podobnie jak przy średniej ruchomej, parametr wygładzania wybieramy stosując kryterium najmniejszego błędu ex post prognoz wygasłych.

3. Prognozy na podstawie modeli wyrównywania wykładniczego

Duże znaczenie praktyczne modeli wyrównywania wykładniczego polega na tym, że nadają się one do konstrukcji prognoz nie tylko w warunkach ustabilizowanego rozwoju interesujących nas zjawisk ekonomicznych, lecz także i wtedy, gdy rozwój ten przebiega w sposób nieregularny, charakteryzujący się załamaniami trendu. W modelach tych nie przyjmuje się stałej postaci analitycznej trendu, lecz przeciwnie, zakłada się, że dla każdego okresu ocenę poziomu trendu i ewentualnych wahań periodycznych buduje się jako pewną przeciętną z tego rodzaju ocen dokonanych w poprzednich okresach. Spośród wielu znanych w literaturze modeli wykorzystane zostaną: modele Browna: model liniowy i model kwadratowy, model liniowy Holta, oraz model z dwoma parametrami wyrównywania (stosowany zarówno w przypadku trendów liniowych i jak i nieliniowych). Wartość prognostyczna modeli zostanie określona ex post po obliczeniu wartości bezwzględnych błędów prognoz na podstawie miary MAE.

Dla zadanego szeregu czasowego prognoza zostanie wyznaczona na podstawie modelu, dla którego miara ta będzie najmniejsza.

3.1. MODEL LINIOWY BROWNA

Do wygładzenia szeregu czasowego, w którym występują i tendencja rozwojowa i wahania przypadkowe można wykorzystać jeden z modeli Browna. Jeżeli do opisu trendu wykorzystamy wielomian stopnia pierwszego, podstawowe równania modelu są następujące:

Najczęściej przyjmujemy:

Prognozy na okres t+h, dla h≥ 1 obliczamy ze wzoru:

3. 2. MODEL NIELINIOWY Z DWOMA PARAMETRAMI

Model ten znajduje zastosowanie zarówno w przypadku trendu liniowego jak i nieliniowego. Jest on bardziej elastyczny w porównaniu z modelami Browna ze względu na występowanie dwóch parametrów wygładzania.

Parametry wyrównywania:

• 0 ≤ a < 1, na podstawie którego wyliczamy dwa inne parametry odpowiedzialne za wyrównanie:

1. poziomu: a*(2-a)

1. trendu : a²

• d∈< 0,5; 1,2> ; parametr ten decyduje o wyborze postaci funkcji trendu (dla t=1 mamy do czynienia z funkcją liniową)

Ocenę wyrównanego poziomu i przyrostu trendu badanej zmiennej na poziomie zerowym i odpowiednio na poziomie t znajdujemy z równań:

Poziom₀ = y₁ Trend₀=(y₂-y₁)

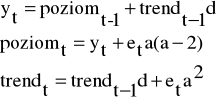
Pierwszą prognozę obliczamy ze wzoru:

Natomiast do obliczenia następnych prognoz (h>1) stosujemy wzór:

3.3. MODEL LINIOWY HOLTA

Model ten stosowany jest w przypadku wystepowania trendu liniowego. Ze względu na występowanie dwóch parametrów wyrównywania jest bardziej elastyczny niż przedstawiony wcześniej model liniowy Browna.

Podstawowe równania modelu są następujące:

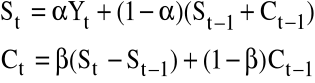
Najczęściej przyjmujemy:

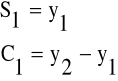
Prognozy obliczamy z następującego wzoru:

3.4. MODEL WINTERSA

Model Wintersa może być stosowany do prognozowania , gdy szereg czasowy zawiera trend, wahania sezonowe oraz wahania przypadkowe. Równania addytywnej wersji modelu są następujące:

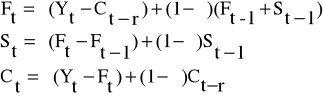
gdzie:

F_t - ocena wartości średniej

S_t - ocena przyrostu trendu

C_t - ocena wahania sezonowego

r - liczba sezonów w ramach cyklu

α, β, γ - parametry modelu z przedziału [0; 1]

Równania prognozy są następujące:

Za wartości początkowe można przyjąć odpowiednio:

• za F₁ pierwszą wartość zmiennej y, tj. y₁

• za S₁ różnicę drugiej i pierwszej wartości zmiennej y, tj. y₂ - y₁

• za C₁, C₂, ... C_r wyznaczone na podstawie całego szeregu czasowego surowe wskaźniki sezonowości.

2. Analiza wahań okresowych

Metody budowy modeli uwzględniających wahania okresowe:

1. metoda wskaźników

2. metoda L. R. Kleina (1965r) wykorzystująca zmienne zero-jedynkowe

3. metoda trendów jednoimiennych

4. analiza harmoniczna

4.1. Metoda wskaźników

Do opisu kształtowania się wartości prognozowanej można użyć modelu:

1. addytywnego, gdy amplitudy wahań w analogicznych fazach cyklu są w przybliżeniu takie same

gdzie:

y_ti - rzeczywista wartość zmiennej prognozowanej w okresie t w i-tej

fazie cyklu

- teoretyczna wartość zmiennej prognozowanej w okresie t w i-tej

fazie cyklu, wyznaczona z modelu tendencji rozwojowej

c_i - efekt okresowy w i-tej fazie cyklu

r - liczba faz cyklu

2. multyplikatywnego, gdy wielkości amplitud wahań zmieniają się mniej więcej w tym samym stosunku w analogicznych fazach cyklu

W analizie wskaźnikowej można wyróżnić cztery etapy prac:

• wyodrębnienie tendencji rozwojowej

• eliminację tendencji rozwojowej z szeregu czasowego

• eliminację oddziaływania wahań przypadkowych

• obliczanie czystych wskaźników sezonowości

4.2. Metoda L. R. Kleina (1965r) wykorzystująca zmienne zero-jedynkowe

Postać modelu:

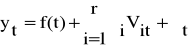
(1)

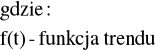
V_it - i-ta zmienna zero-jedynkowa, przyjmująca wartość jeden dla fazy o

numerze i oraz zero dla pozostałych faz cyklu

r- liczba faz cyklu

Z definicji wahań periodycznych wynika, że: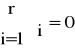
, więc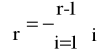
.

Ostatecznie otrzymujemy model:

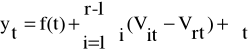
(2)

Parametry modelu są szacowane metodą najmniejszych kwadratów.

4.3. Metoda trendów jednoimiennych

Metoda ta polega na budowie modeli tendencji rozwojowej oddzielnie dla poszczególnych faz cyklu. Jeżeli przez r oznaczymy liczbę faz cyklu, to postać budowanego modelu jest następująca:

gdzie:

y_ti - rzeczywista wartość zmiennej prognozowanej w okresie t w i-tej

fazie cyklu

f_i (t_i) - funkcja trendu dla i-tej fazy cyklu

Literatura:

1. Barczak A.S., Biolik J., (2001), Podstawy ekonometrii, AE Katowice, Katowice.

2. Decyzje menedżerskie z Excelem, (2000), Red. T. Szapiro, PWE, Warszawa.

3. Dittman P., (2003), Prognozowanie w przedsiębiorstwie, Oficyna Ekonomiczna, Kraków.

4. Metody prognozowania. Zbiór zadań, (1999), Red. B. Radzikowska, Wydawnictwo, A.E. im. O. Langego we Wrocławiu

5. Prognozowanie gospodarcze - metody i zastosowania, (1997), Red. M. Cieślak, Wydawnictwo Naukowe PWN, Warszawa.

6. Zeliaś A., Pawełek B., Wanat S., (2003), Prognozowanie ekonomiczne - teoria, przykłady, zadania, Wydawnictwo Naukowe PWN, Warszawa.

1

32

Wykładowca:

Dr. Maria Jadamus- Hacura

---