Wyznaczanie promienia krzywizny soczewki za pomocą pierścieni Newtona.

1. Wstęp teoretyczny:

Kołowe pierścienie interferencyjne, zwane pierścieniami Newtona, powstają, gdy równoległa wiązka światła pada na układ złożony z dokładnie płaskiej płyty szklanej oraz leżącej na niej soczewki o promieniu krzywizny R (rys. obok).

Między soczewką i płytą znajduje się warstwa powietrza o grubości d wzrastającej ze wzrostem odległości od osi układu.

Obraz interferencyjny powstaje w wyniku nałożenia promieni odbitych od dolnej powierzchni soczewki i od górnej powierzchni płyty.

Różnica dróg geometrycznych obu promieni wynosi 2d. Dla obliczenia dróg optycznych przyjmujemy, że współczynnik załamania powietrza jest równy jedności, a także uwzględniamy fakt, że odbiciu od ośrodka gęstszego towarzyszy zmiana fazy o
, czemu odpowiada dodatkowa różnica dróg
.

Biorąc powyższe pod uwagę możemy napisać warunek powstania jasnego pierścienia interferencyjnego.

(1).

Na podstawie rysunku możemy grubość warstwy powietrznej przez promień pierścienia interferencyjnego

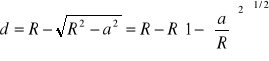
(2).

Jeżeli a/R<<1, to można powyższe wyrażenie przedstawić w postaci

(3).

Łącząc powyższe równanie z równaniem (1) otrzymamy

(4).

Otrzymane równanie określa promienie jasnych prążków interferencyjnych.

W miejscu zetknięcia się soczewki z płytą tworzy się bardzo cienka warstwa powietrza, o grubości wielokrotnie mniejszej od długości fali. Różnica dróg optycznych powstająca między promieniami w tym punkcie jest skutkiem jedynie straty połowy długości fali przy odbiciu od płyty. W rezultacie wynosi ona
- w środku obrazu interferencyjnego obserwujemy ciemne pole.

Jeżeli układ oświetlamy światłem białym, powstają barwne pierścienie, które przy wyższych rzędach m zachodzą na siebie.

W celu wyznaczenia promieni pierścieni Newtona posługujemy się przystosowanym do tego celu mikroskopem. Płytę z soczewką umieszczamy w polu widzenia mikroskopu na stoliku przesuwanym w poziomie w dwóch kierunkach za pomocą dwóch śrub mikrometrycznych. Aby umożliwić jednoczesne oświetlenie układu i obserwację obrazu, na osi optycznej mikroskopu M umieszczamy płytkę przeźroczystą P nachyloną pod katem 45⁰ do kierunku biegu promieni. Płytka odbija część promieni pochodzących za źródła S kieruje je do układu, gdzie ulegają odbiciu i interferencji, po czym przechodzą przez płytkę P do obiektywu mikroskopu.

Okular mikroskopu jest zaopatrzony w krzyż z nitek pajęczych, dzięki czemu możemy precyzyjnie ustawić wybrany fragment obrazu w polu widzenia. Przesuwając stolik wzdłuż linii przechodzącej przez środek obrazu tylko w kierunku X, można znaleźć położenia pierścieni po prawej a_p i po lewej a_l stronie od środka. Promień prążka rzędu m obliczymy jako połowę średnicy:

(5).

Jeżeli związek (4) przekształcimy do postaci

(6),

to widać, że porzyteczne będzie sporządzenie wykresu we współrzędnych y = a² , x = (m-1/2),

ponieważ wykresem będzie wtedy linia prosta. Współczynnik nachylenia wynosi λR . Wartość tego współczynnika znajdziemy z regresji liniowej; zaznaczmy ją a_r. Z przyrównania otrzymamy ostatecznie wartość szukanego promienia krzywizny soczewki:

(7).

Wartość λ = 589 [nm]

2. Przebieg ćwiczenia

1. Za pomocą śrub przesuwu stolika zmierzyć położenie kolejnych jasnych pierścieni po prawej stronie względem środka. To samo zrobić dla lewych krawędzi pierścieni. Pomiary wykonać dla wszystkich dających się zmierzyć pierścieni.

2. Obliczyć promienie pierścieni.

3. Zrobić wykres
   .

4. Obliczyć współczynnik nachylenia i jego błąd, stosując regresję liniową. Jeżeli część punktów pomiarowych odbiega od linii prostej, to te punkty należy odrzucić. Najbardziej prawdopodobną przyczyną nieliniowości jest deformacja soczewki w pobliżu punktu styczności z płytą, spowodowana nadmiernym dociskiem. Wynikiem tego jest powiększenie promieni pierścieni niskich rzędów.

5. Wyznaczyć promień krzywizny soczewki na podstawie równania (7).

6. Obliczyć błąd metodą różniczki zupełnej lub logarytmicznej.

7. Zaokrąglić wyniki obliczeń i podać ostateczną postać.

3. Wyniki pomiarów i obliczenia:

Nr pierścienia	Położenie po lewej [mm]	Położenie po prawej [mm]	Promień pierścienia [mm]
1	27,05	24,22	1,42
2	27,28	24,03	1,63
3	27,46	23,77	1.85
4	27,59	23,61	1,99
5	27,68	23,50	2,09
6	27,85	23,37	2,24
7	27,97	23,27	2,35
8	28,08	23,14	2,47
9	28,20	23,02	2,59
10	28,28	22,94	2,67

Za pomocą programu StatS wyznaczyłem współczynnik nachylenia a_r = 0,5646^. 10 ^-6 ,

oraz jego błąd Δa_r = 0,0104 ^. 10 ^-6 .

Ze wzoru (7) (przyjmując za λ = 589 [nm]) obliczamy promień krzywizny soczewki:

Błąd promienia krzywizny wyniesie:

Ostatecznie promień krzywizny soczewki wynosi:

4. Wnioski

Otrzymany wynik wydaje się do zaakceptowania. Błąd nie jest duży. Może on wynikać z niedokładności odczytu poszczególnych odchyleń. Wpływ na niego ma też znaczna szerokość promieni niskich rzędów, co utrudnia znalezienie ich środka. Uważam, że cel doświadczenia został osiągnięty.

---