Charakterystyki geometryczne poszczególnych figur:

Figura nr1

h =8 cm ; b = 6 cm

A₁ =
∙ b∙h

A₁ =
∙ 6∙8 = 24 cm²

I_x1 =
=
= 85,3 cm⁴

I_y1 =
=
= 48 cm⁴

D_x1y1 =
= -32 cm⁴

e_x= 4cm ; e_y= 5,4 cm

Figura nr2

h =8 cm ; b = 6 cm

A₂ =
∙ b∙h

A₂ =
∙ 6∙8 = 24 cm²

I_x2 =
=
= 85,3 cm⁴

I_y2 =
=
= 48 cm⁴

D_{x2y 2}=
= 32 cm⁴

e_x=4 cm ; e_y= 2,6 cm

Figura nr3

skala 1:2

b = 2 cm ; h = 14 cm

A₃ = b∙h

A₃ = 2∙14 = 28 cm²

I_x3 =
=
= 457,3 cm⁴

I_y3 =
=
= 9,3 cm⁴

D_{x3y 3} = 0

e_x=1 cm ; e_y= 7 cm

Figura nr4

skala 1:2 b = 14 cm ; h = 14 cm

A₄ =
∙ b∙h

A₄ =
∙14∙14= 98 cm²

I_x4 =
=
= 1067,1 cm⁴

I_y4 =
=
= 1067,1 cm⁴

D_{x4y 4}=
=
= 533,5cm⁴

e_x = 14∙
= 4,6 cm

e_y = 14 - 4,6 = 9,4 cm

Figura nr5

r = 2 cm

A₅ =
=
= 3,14 cm²

I_x5 = I_y5 = 0,05488∙r²

I_x5 = I_y5 = 0,05488∙4 = 0,87808 cm⁴

e_x = e_y = 0,4244∙r

e_x = e_y = 0,4244∙2 = 0,8488 cm

D_{x5y 5} = 0,01647∙r⁴

D_{x5y 5} = 0,01647∙16 = 0,26352 cm⁴

Figura nr6

skala 1:2

b= 8,2 cm ; h= 18 cm

A₆ = 27,9 cm²

I'_x6 = 1450 cm⁴

I'_y6 = 81,3 cm⁴

D'_x6y6 = 0

e_x= 4,1 cm ; e_y= 9 cm

I_x6 =
+
∙ cos2α - D'_x6y6∙sin2α α = 45°;cos2α = 90° ;cos90°= 0

I_x6 =
0 - 0 = 765,65 cm⁴ sin90°= 1

I_y6 =
-
∙ cos2α + D'_x6y6∙sin2α

I_y6 =
0 + 0 = 765,65 cm⁴

D_x6y6 =
∙sin2α + D'_x6y6 cos2α

D_x6y6 =
1 + 0 = 684,35 cm⁴

Obliczenie sumy wszystkich pól powierzchni:

= A₁+A₂+A₃+A₄+A₅+A₆

= 24 + 24 + 28 + 98 + 3,14 + 27,9 =205,04 cm²

Współrzędne środków ciężkości figur:

x₁= 6-2 =4 cm y₁=0,9+8-2,6 = 6,3 cm

x₂= 6-2 =4 cm y₂=0,9+8+2,6=11,5 cm

x₃= 6+1=7 cm y₃=0,9+2+7=9,9 cm

x₄= 6+2+4,6 = 12,6 cm y₄=0,9+2+(14-4,6)=12,3 cm

x₅= 6 +0,8488 = 6,85 cm y₅=0,9+(2-0,8488)=2,05 cm

x₆= 6+2+2,9+6,3639 = 17,26 cm y₆=6,3639 cm

Obliczenie współrzędnych środka ciężkości:

x_s=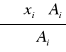

x_s= ( 4∙24 + 4 ∙24 + 7∙28 + 12,6∙98 + 6,85∙3,14 + 17,6∙27,9):205,04

x_s= 10,37 cm

y_s=

y_s=( 6,3∙24 + 11,5∙24 + 9,9∙28 + 12,3∙98 + 2,05∙3,14 + 6,36∙27,9):205,04

y_s= 10,21 cm

nr.	A [cm^2]	xi [cm]	yi [cm]	xiAi [cm^3]	yiAi [cm^3]
1	24	4	6,3	96	151,2
2	24	4	11,5	96	276
3	28	7	9,9	196	277,2
4	98	12,6	12,3	1234,8	1205,4
5	3,14	6,85	2,05	21,509	6,437
6	27,9	17,26	6,3639	481,554	177,55
	205,04	51,71	48,41	2125,863	2093,787

Obliczenie momentów bezwładności i momentów dewiacji

I_x= Σ ( I_xi + y_i²A_i )

I_y= Σ ( I_yi + x_i²A_i )

D_xy= Σ( D_xiyi + x_iy_iA_i )

Figura nr 1:

x_i = x₁ - x_s = 4 - 10,37 = -6,37 cm

y_i = y₁ - y_s = 6,3 - 10,21 = -3,91 cm

Figura nr 2:

x_i = x₂ - x_s = 4 - 10,37 = -6,37 cm

y_i = y₂ - y_s = 11,5 - 10,37 = 1,29 cm

Figura nr 3:

x_i = x₃ - x_s = 7 - 10,37 = -3,37 cm

y_i = y₃ - y_s = 9,9 - 10,21 = -0,31 cm

Figura nr 4:

x_i = x₄ - x_s = 12,6 - 10,37 = 2,23 cm

y_i = y₄ - y_s = 12,3 - 10,37 = 2,09 cm

Figura nr 5:

x_i = x₅ - x_s = 6,85 - 10,37 = -3,52 cm

y_i = y₅ - y_s = 2,05 - 10,21 = -8,16 cm

Figura nr 6:

x_i = x₆ - x_s = 17,26 - 10,37 = 6,89 cm

y_i = y₆ - y_s = 6,3639 - 10,21 = -3,85 cm

nr	Ai [cm^2]	xi [cm]	yi [cm]	Ixi [cm^4]	Iyi [cm^4]	Dxiyi [cm^4]	xi^2Ai [cm^4]	yi^2Ai [cm^4]	xiyiAi [cm^4]
1	24	-6,37	-3,91	85,3	48	-32	973,8456	366,9144	597,7608
2	24	-6,37	1,29	85,3	48	32	973,8456	39,9384	-197,2152
3	28	-3,37	-0,31	457,3	9,3	0	317,9932	2,6908	29,2516
4	98	2,23	2,09	1067,1	1067,1	533,5	487,3442	428,0738	456,7486
5	3,14	-3,52	-8,16	0,878	0,878	0,2635	38,9058	209,0787	90,1908
6	27,9	6,89	-3,85	765,65	765,65	684,35	1324,4715	413,5477	-740,0893
Σ	205,04	-10,51	-12,85	2461,528	1938,928	1218,1135	4116,4059	1460,2438	236,6473

I_x=
+
= 2461,528 + 1460,2438 = 3921,7718 cm⁴

I_y=
+
= 1938,928 + 4116,4059 = 6055,3339 cm⁴

D_xy=
+
= 1218,1135 + 236,6473 = 1454,7608 cm⁴

Położenie głównych centralnych osi bezwładności

tg 2α gł. =
=
=
= 1,3636

2α gł. = 53°44'

α gł. = 26°52'

Główne centralne momenty bezwładności:

I_I = I_max =

I_I =

I_I =
cm⁴

I_II = I_min =

I_II = I_min =

I_II = I_min =
cm⁴

Sprawdzenie:

I_x +I_y = I_I + I_II

3921,7718 + 6055,3339 = 6792,534777 + 3184,570923

9977,1057 = 9977,1057

---