Egzamin pisemny z Teorii Systemów - część teoretyczna. 7 II 2005
Dla filtru dolnoprzepustowego o transmitancji H(s)=1/(s5+a4s4+a3s3+a2s2+a1s+a0), przy częstotliwości 0Hz tłumienie wynosi 0,4dB. Wyznaczyć a0.
Ile wynosi krotność zera transmitancji w s=0 dla filtru górnoprzepustowego, eliptycznego szóstego rzędu?
Naszkicować wykres α(ω) w paśmie przepustowym dla dolnoprzepustowego filtru Czebyszewa 5 rzędu.
Wyznaczyć odpowiedź układu o transmitancji (1+s)/(1+s2) na pobudzenie sygnałem: (grupa pierwsza) u(t)=1(t)e-2t , (grupa druga) u(t)=1(t)e-3t y(t)=......
Podaj wzór na transmitancję regulatora w układzie PI.
W stabilnym układzie wszechprzepustowym pierwszego rzędu biegun położony jest na okręgu jednostkowym. Oblicz opóźnienie grupowe dla ω=1rad/s.
Podaj wzór na transmitancję układu LTI na podstawie macierzy stanu A, B, C, D.
Źródło napięciowe idealne E=5V obciążono odbiornikiem nieliniowym o charakterystyce U=2+(I-1)2, gdzie natężenie prądu jest wyrażone w [mA] a napięcie w [V], do rozwiązania przyjęto metodę Newt.-Raph. Punkt startowy przyjęto I0=2mA. Wyznaczyć kolejne przybliżenie I1= .....
Narysować 2 alternatywne schematy układu dolnoprzepustowego filtru Czebyszewa rzędu 7 zrealizowanego jako obustronnie obciążony czwórnik drabinkowy filtru LC.
Czy układ:
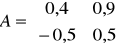
, 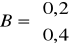
, ![]()
, ![]()
jest stabilny asymptotycznie? Odpowiedź krótko uzasadnij.
Dla bardzo dużych częstotliwości podać nachylenie charakterystyki amplitudowej dla filtru pasmowoprzepustowego Butterwortha 6 rzędu ……………dB/oktawę.
Dla filtru dolnoprzepustowego Czebyszewa 4 rzędu znany jest parametr ε = 0,1. Oblicz αp.
Układ otwarty trzeciego rzędu zamknięto w pętli ujemnego sprzężenia zwrotnego o jednakowym wzmocnieniu. Dla układu otwartego |H(jω)|=0,4, gdy ϕ=arg[H(jω)]=-π. Ile razy może zwiększyć się współczynnik wzmocnienia układu otwartego by układ zamknięty pozostał stabilny?
Ile wynosi krotność zera transmitancji w s=0 dla filtru górnoprzepustowego, eliptycznego piątego rzędu?
Naszkicować α(ω) w paśmie przepustowym dla filtru pasmowoprzepustowego Czebyszewa rzędu 4.
odpowiedź układu o transmitancji (1+s)/(1+s2) na pobudzenie sygnałem: 1(t)e-3t ,y?
Dla odpowiedzi skokowej g(t) regolatora PI zachodzi g(1)=2 oraz limt->0+g(t)=1. Podać odpowiedź impulsową tego regulatora: h(t)= ......
W stabilnym układzie wszechprzepustowym pierwszego rzędu biegun położony jest na okręgu jednostkowym. Oblicz opóźnienie grupowe dla ω=2rad/s.
tu było jakieś dziwne zadanie z K(s)=F(s)/B(s)…
Źródło napięciowe idealne E=8V obciążono odbiornikiem nieliniowym o charakterystyce U=2+(2I-2)2, gdzie natężenie prądu jest wyrażone w [mA] a napięcie w [V], do rozwiązania przyjęto metodę Newt.-Raph. Punkt startowy przyjęto I0=1mA. Wyznaczyć kolejne przybliżenie I1= .....
Narysować 2 alternatywne schematy układu górnoprzepustowego filtru Czebyszewa rzędu 7 zrealizowanego jako czwórnik drabinkowy filtru LC.
Czy układ:
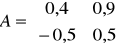
, 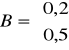
, ![]()
, ![]()
jest stabilny asymptotycznie? Odpowiedź krótko uzasadnij.
zadania z poprawki:
część teoretyczna
1) Dla bardzo dużych częstotliwości wyznacz nachylenie charakterystyki amplitudowej pasmowoprzepustowego filtru Butterwortha szóstego rzędu
2) Wyznacz maksymalne tłumienie w paśmie przepustowym dla dolnoprzepustowego filtru Czebyszewa czwartego rzędu (podany epsilon)
3) Ile wynosi krotność zera transmitancji w s = 0 dla górnoprzepustowego filtru eliptycznego piątego rzędu?
4) Wykres dla pasmowoprzepustowego filtru Czebyszewa czwartego rzędu
5) Wyznaczyć odpowiedź układu o podanej transmitancji na pobudzenie podanym sygnałem
6) Wyznaczyć tłumienie dla pulsacji omega = 0, przy podanych zerach tłumienia i zerach transmisji
7) Narysować dwa alternatywne schematy układu górnoprzepustowego filtru Czebyszewa siódmego rzędu zrealizowanego jako czwórnik drabinkowy filtru LC
część zadaniowa:
8) dla układu określonego danymi parametrami
a)sprawdzić, czy układ jest stabilny w sensie Lapunowa
b)wyznaczyć zmienną stanu x1(t) jako funkcję czasu t
9) Graf
a)wyznaczyć transmitancję H(s) korzystając z reguły topologicznej Masona
b)podać równania stanu
10) Wykorzystując aproksymację Butterwortha wyznaczyć transmitancję filtru spełniającego podane wymagania odnoszące się do charakterystyki amplitudowej. Wyznaczyć tłumienie (w decybelach) sygnału x(t)=4cos(2t) po przejściu przez zaprojektowany filtr.
Test- pierwsza część egzaminu z Teorii Systemów u Domańskiego (30.01.2003)
dobra odpowiedź 2pkt.; zła 0pkt.
# Dla filtru dolnoprzepustowego o transmitancji H(s)=1/(s5+a4s4+a3s3+a2s2+a1s+a0), przy częstotliwości 0Hz tłumienie wynosi 0,4dB. Wyznaczyć a0.
# Ile wynosi krotność zera transmitancji w s=0 dla filtru górnoprzepustowego, eliptycznego piątego rzędu?
# Naszkicować wykres α(ω) w paśmie przepustowym dla dolnoprzepustowego filtru Czybyszewa 4 rzędu (dla pierwszej grupy) /5 rzędu (dla drugiej grupy).
# Układ otwarty trzeciego rzędu zamknięto w pętli ujemnego sprzężenia zwrotnego o jednakowym wzmocnieniu. Dla układu otwartego |H(jω)|=0,8, gdy ϕ=arg[H(jω)]=-π. Ile razy może zwiększyć się współczynnik wzmocnienia układu otwartego by układ zamknięty pozostał stabilny?
# Wyznaczyć odpowiedź układu o transmitancji (2+s)/(1+s2) na pobudzenie sygnałem:
grupa pierwsza) 1(t)e-2t grupa druga) 1(t)e-3t y(t)= ......
# Część rzeczywista transmitancji widmowej układu rzeczywistego została zapisana jako wielomian postaci a0+a1ω+a2ω2+a3ω3+a4ω4, wyznaczyć wartości dwóch współczynników ai.
# Dla odpowiedzi skokowej g(t) regolatora PI zachodzi g(1)=2 oraz limt->0+g(t)=1. Podać odpowiedź impulsową tego regulatora: h(t)= ......
# Źródło napięciowe idealne E=5V obciążono odbiornikiem nieliniowym o charakterystyce U=5t(I-3)2 (tego nie jestem pewien), gdzie natężenie prądu jest wyrażone w [mA] a napięcie w [V], do rozwiązania przyjęto metodę Newt.-Raph. Punkt startowy przyjęto I0=4mA. Wyznaczyć kolejne przybliżenie I1= .....
# Czy z samych oporników można zbudować sieć neuronową: TAK / NIE (+uzasadnienie).
# Napisz przykładowy wzór na transmitancję stabilnego (BIBO) układu wszechprzepustowego o trzech biegunach rzeczywistych. H(s)= .........
1.H(s)=1/ ( s^5 +a4s^4 ...+ a0 )
przy czest w 0 Hz tlumnienie wynosi L 0 0,4 ile wynosi a0 ?
2.ile wynosi krotnosc zera transmisji w s = 0 dla f. eliptycznego HP
6 rzedu
3. wykres LP f. czybyszewa
4. uklad otwaryty o transmitancji /H(jw)/ = 05 , fi = - pi . ile razy
mozna wzmocnic uklad aby byl on stabilny ?
5. H(s) = ( s(s+3) ) / (1+s^2)
u(t) = e^(-3t)
y(t) = ????
6. cz rzeczywista transmitancji zapisano jako wielomian w postaci :
a0 + a1w + a2w^2 ... a4w^4 - wyznaczyc 2 wspolcznynniki ai ?
7. dla odpowiedzi skokowej g(t) regulatora PI zachodzi rownianie g(1)
= 3 , g(t) ( t->0 ) = 2
odpowiedz impulsowa regulatora PI to :
8. uklad nieliniowy - podobny do tego co bylo rok temu
9. czy z samych opornikow i kondensatorow mozna zbudowac siec
neuronowa ? uzasadnic
10 podac uklad wszechprzepustowy o 2 rzeczywistych biegunach (
stabilny BIBO ) :
11. podac wzor na transpormate czestotl. tworzaca z transmitancji LP
filtr BP
1. Dla układu o transmitancji operatorowej ![]()
wyznaczyć wzór określający opóźnienie grupowe w funkcji pulsacji.
2. Dla filtru o transmitancji ![]()
, dla dużych wartości częstotliwości należy wyznaczyć nachylenie wykresu tłumienia w funkcji pulsacji w skali logarytmicznej.
3. Napisać wzór określający transmitancję operatorową układu LTI w zależności od macierzy opisu w przestrzeni zmiennych stanu.
4. Starannie narysować wykres ![]()
w paśmie zaporowym dla filtru eliptycznego siódmego rzędu. Narysować odpowiednią linię łączącą ekstrema wykresu.
5. Dla pewnego filtru mającego wszystkie zera transmitancji w nieskończoności transmitancja spełnia zależność ![]()
, gdzie ![]()
jest wielomianem szóstego stopnia. Wyznaczyć bieguny transmitancji.
6. Podaj wzór określający wektor stanu ![]()
układu dyskretnego jako funkcję numeru próbki w czasie dla układu równań stanu ![]()
przy warunkach początkowych ![]()
7. Dla odpowiedzi skokowej ![]()
(odpowiedzi na skok jednostkowy) regulatora PI zachodzi ![]()
, ![]()
. Odpowiedź impulsowa tego regulatora ![]()
8. Źródło napięcia idealne o ![]()
obciążono odbiornikiem nieliniowym o charakterystyce ![]()
, gdzie natężenie prądu jest wyrażone w [mA], a napięcie w [V]. Do rozwiązania zastosowano metodę Newtona - Raphsona. Punkt startowy przyjęto ![]()
. Wyznaczyć kolejne przybliżenie ![]()
9. Dla stanu równowagi podać definicję stabilności w sensie Lapunowa.
10. Proszę napisać przykładowy wzór na transmitancję stabilnego (BIBO) układu wszechprzepustowego o trzech biegunach rzeczywistych. ![]()
(we wzorze mają występować współczynniki określone konkretnymi liczbami.
1. Dla układu o transmitancji operatorowej ![]()
wyznaczyć wzór określający opóźnienie grupowe w funkcji pulsacji.
2. Dla filtru o transmitancji 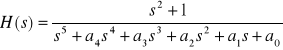
, dla dużych wartości częstotliwości należy wyznaczyć nachylenie wykresu tłumienia w funkcji pulsacji w skali logarytmicznej.
3. Napisać wzór określający transmitancję operatorową układu LTI w zależności od macierzy opisu w przestrzeni zmiennych stanu.
4. Starannie narysować wykres ![]()
w paśmie zaporowym dla filtru eliptycznego szóstego rzędu. Narysować odpowiednią linię łączącą ekstrema wykresu.
5. Dla pewnego filtru mającego wszystkie zera transmitancji w nieskończoności transmitancja spełnia zależność ![]()
, gdzie ![]()
jest wielomianem szóstego stopnia. Wyznaczyć bieguny transmitancji.
6. Podaj wzór określający wektor stanu ![]()
układu dyskretnego jako funkcję numeru próbki w czasie dla układu równań stanu ![]()
przy warunkach początkowych ![]()
7. Dla odpowiedzi skokowej ![]()
(odpowiedzi na skok jednostkowy) regulatora PI zachodzi ![]()
, ![]()
. Odpowiedź impulsowa tego regulatora ![]()
8. Źródło napięcia idealne o ![]()
obciążono odbiornikiem nieliniowym o charakterystyce ![]()
, gdzie natężenie prądu jest wyrażone w [mA], a napięcie w [V]. Do rozwiązania zastosowano metodę Newtona - Raphsona. Punkt startowy przyjęto ![]()
. Wyznaczyć kolejne przybliżenie ![]()
9. Dla stanu równowagi podać definicję stabilności w sensie Lapunowa.
10. Proszę napisać przykładowy wzór na transmitancję stabilnego (BIBO) układu wszechprzepustowego o trzech biegunach rzeczywistych. ![]()
(we wzorze mają występować współczynniki określone konkretnymi liczbami.
αp
ωp1 ωp2
Wyszukiwarka
Podobne podstrony:
filtry2, Elektronika i Telekomunikacja, semestr 3, teoria systemow
filtry1, Elektronika i Telekomunikacja, semestr 3, teoria systemow
zadania 2(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 9(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 7(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 5(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Teor
zadania 6(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 4(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 8(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
zadania 3(1), WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, Zadania i Te
Sys kom lab harmonogram zao2015 E3, WAT- Elektronika i Telekomunikacja, Semestr V, Systemy Komutacyj
opracowane kolos, WAT- Elektronika i Telekomunikacja, Semestr I, Pnor, Pnor
sciaga algebra wzory, WAT- Elektronika i Telekomunikacja, Semestr I, Matematyka, Algebra z Geometrią
Test B, WAT- Elektronika i Telekomunikacja, Semestr II, Materiały elektroniczne, kolos
WSTĘP TEORETYCZNY, WAT- Elektronika i Telekomunikacja, Semestr II, Fizyka, coś tam od grupy, labfizy
Egzaminacyjne dane przez Pluta, WAT- Elektronika i Telekomunikacja, Semestr II, Elementy elektronicz
więcej podobnych podstron