potęgi i pierwiastki
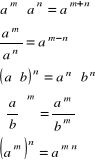
wzory skróconego mnożenia
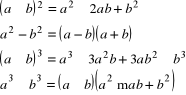
funkcja wykładnicza i logarytmiczna
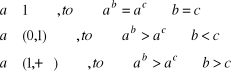
działania na logarytmach
funkcje trygonometryczne
wartości f.tryg. dla podstawowych kątów
tabela znaków f.tryg. w przedziałach
podstawowe zależności
postać ogólna y = ax2 + bx + c
postać kanoniczna y = a(x - p)2 + q
postać iloczynowa: y = a(x - x1)(x - x2)
wzory Viete'a ( ∆ > 0 )
Twierdzenie Bezouta.
monotoniczność
asymptoty
trójkąty
czworokąty
okrąg i koło
bryły
punkt i prosta
dwie proste:
wektory
równanie okręgu
x |
30o |
45o |
60o |
sin |
|
|
|
cos |
|
|
|
tg |
|
1 |
|
ctg |
|
1 |
|
x |
(0;90o) |
(90;180) |
(180;270) |
(270;360) |
sin |
+ |
+ |
- |
- |
cos |
+ |
- |
- |
+ |
tg |
+ |
- |
+ |
- |
ctg |
+ |
- |
+ |
- |
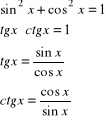
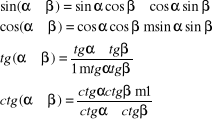

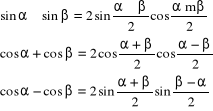
funkcja kwadratowa
![]()
; ![]()
( p , q ) - wierzchołek paraboli o ramionach skierowanych ku górze (a>0) lub w dół (a<0).
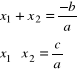
wielomiany
Liczba r jest pierwiastkiem wielomianu W(x) wtedy i tyko wtedy, gdy wielomian W(x) jest podzielny przez (x - r)
kombinatoryka

jeżeli dla każdego x∈(a;b)
- f'>0, to funkcja f jest rosnąca w przedziale (a;b).
- f'<0, to funkcja f jest malejąca w przedziale (a;b).
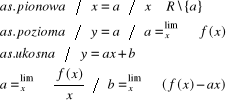
geometria klasyczna
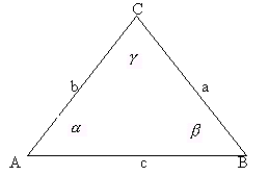
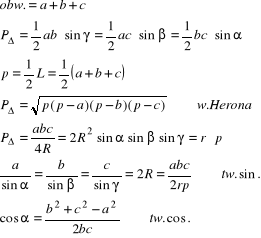
- trójkąt równoboczny
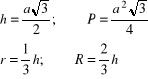
δ - kąt między przekątnymi
![]()
![]()
- graniastosłup dowolny
![]()
- ostrosłup dowolny
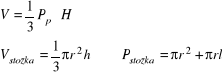
- kula
![]()
geometria analityczna
![]()
- równanie prostej przechodzącej przez punkty A i B
![]()
- odległość punktu A od prostej
![]()
l; A1x + B1y + C = 0 k; A2x + B2y + C = 0
- są równoległe, gdy A1B2 - A2B1 = 0
- są prostopadłe, gdy A1A2 + B1B2 = 0
- kąt przecięcia się prostych, gdy: B1 = B2 = -1
![]()
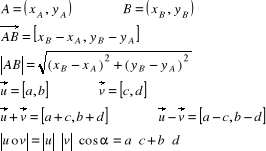
- pole równoległoboku powstałego ze złożenia wektorów u i v (tak jak w regule równoległoboku)
![]()
(x - a)2 + (y - b)2 = r2
ciągi
ciąg rosnący - an+1 - an > 0
ciąg malejący - an+1 - an < 0

Wyszukiwarka
Podobne podstrony:
zarzadzanie piatek 1 czerwca, Zarządzanie i inżynieria produkcji, Semestr 2, Podstawy Zarządzania
Statystyka TEST, Zarządzanie i inżyniernia produkcji, Statystyka
Lista noblistów i osób realizujących projekty, PWR, Zarządzanie i inżynieria produkcji, Makroekonomi
Badania makro i mikrostruktury metali i stopów, WIP zarządzanie i inżynieria produkcji, sesja 1, Mat
Zaliczenie z ekonomii, WIP zarządzanie i inżynieria produkcji, sesja 1, pyt
mame, WIP zarządzanie i inżynieria produkcji, sesja 1, Materiały Metalowe, 1111
sckolos2, Studia, Zarządzanie i Inżynieria Produkcji, Metrologia
Tabela[2], Zarządzanie i inżynieria produkcji, Semestr 4, Mechanika Stosowana
spr z ZP, Zarządzanie i inżynieria produkcji, Semestr 4, Zarządzanie personelem
dyrektywy nowego podejscia lista, Zarządzanie i Inżynieria Produkcji - studia, Jakość
ściaga ekonomia, WIP zarządzanie i inżynieria produkcji, sesja 1, ekonomia
operacje gospodarcze, Zarządzanie i inżyniernia produkcji, Rachunkowość
Zgrzewanie, Studia, Zarządzanie i Inżynieria Produkcji, Procesy Polimerowe
Grafika inżynierska - wyklady - 2, Akademia Morska w Szczecinie, Zarządzanie i Inżynieria Produkcji
zarzadz-strategiczne, Politechnika Częstochowska kier. Zarządzanie i Inżynieria Produkcji - prace, r
sciaga moja na tel, WIP zarządzanie i inżynieria produkcji, sesja 1, ekonomia
więcej podobnych podstron