SATLA BARTOSZ	Ćwiczenie nr C4 Temat: Wyznaczanie ciepła metodą Clementa -Desormesa
FIZYKA I ROK	Ocena z kolokwium	Ocena ze sprawozdania	Ocena końcowa
Dr E. Jakubczyk

1. CZĘŚĆ TEORETYCZNA

Równanie stanu gazu doskonałego.

Gazem doskonałym nazywamy tylko gaz:

• składający się z poruszających się chaotycznie cząsteczek o bardzo małych rozmiarach (mają one cechy punktów materialnych)

• cząsteczki te oddziałują ze sobą podczas zderzeń sprężystych (oddziaływanie na odległość można zaniechać)

Stan gazu jest określany przez podanie jego trzech parametrów: temperatury T, objętości V, i ciśnienia p, pod jakim gaz się znajduje. Tych trzech wielkości nie można zmieniać w sposób dowolny, jeżeli masa gazu pozostaje bez zmian. Są one związane ze sobą tzw. równaniem gazu doskonałego.

Dla gazu doskonałego równanie stanu gazu, tj. zależność miedzy ciśnieniem, objetością i temperaturą ma postać:

Wzór ten wynika z trzech doświadczalnie znalezionych praw: prawa Boyle'a Mariotte'a, prawa Gay -Lussaca i ptawa Charlsa.

Z równania stanu gazu doskonałego wynika, że dla stałej masy gazu parametry jego stanu mogą się zmieniać, jednak iloczyn ciśnienia i objętości podzielony przez temperaturę musi mieć stałą wartości (czyli zmiana któregokolwiek z parametrów musi spowodować zmianę pozostałych wielkości tak aby wyrażenie nie zmieniało wartości).

PRZEMIANY GAZOWE

Jeżeli ulegają zmianie przynajmniej dwa z trzech parametrów opisujące stan termodynamiczny określonej masy gazu, to mówimy że gaz ten podlega przemianie termodynamicznej. Szczególnym przypadkiem przemian gazowych są izoprzemiany (przemiana izotermiczna, izobaryczna, izochoryczna).

1. Przemiana izotermiczna T=const

Oprócz stałej masy gazu stała jest temperatura (T1=T2), zmienia się ciśnienie i objętość.

p₁V₁=p₂V₂

Prawo Boyle'a Mariotte'a

W stałej temperaturze ciśnienie danej masy gazu doskonałego jest odwrotnie proporcjonalne do jego objętości.

p

V

Krzywa (hiperbola) przedstawiającą zależność ciśnienia gazu od jego objętości w stałej temperaturze można nazywa się izotermą.

Podczas przemiany izotermicznej energia wewnętrzna gazu nie zmienia się. Z pierwszej zasady termodynamiki wynika, że przy izotermicznym sprężaniu siły zewnętrzne wykonują nad gazem pracę, natomiast gaz oddaje ciepło w ilości równej wykonanej nad nim pracy. W czasie izotermicznego rozprężenia gaz pobiera ciepło i wykonuje pracę o wartości równej pobieranemu ciepłu.

bo T=const.

Dla izotermicznego sprężania:0

O=W-Q więc

Dla izotermicznego rozprężania:

O=-W+Q więc

2. Przemiana izobaryczna p=const.

Oprócz stałej masy gazu, stałe jest ciśnienie (p₁=p₂), zmienia się temperatura i objętość.

Prawo Gay-Lussaca p = const.

Przy stałym ciśnieniu objętość danej masy gazu doskonałego jest wprost proporcjonalna do jego temperatury bezwzględnej, tzn.

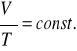
lub

objętość gazu w temp 0⁰C

T

p₁

p₂<p₁

V

Pół prosta przedstawiająca zależność gazu od temperatury w stałym ciśnieniu nazywa się izobarą. Podczas izobarycznego ogrzewania gaz pobiera ciepło i wykonuje pracę, przy czym wartość popranego ciepła jest większa od wartości wykonanej pracy wzrost temp czyli wzrost energii. wew.)

więc

w czasie izobarycznego oziębiania gaz oddaje ciepło, a siły zewnątrzne wykonująnad nim pracę (sprężają go) przy czym wartość oddanego ciepła jest większa niż wartość wykonanej pracy.

więc

2. Przemiana izochoryczna V=const.

Oprócz stałej masy gazu stała jest objętość (V₁=V₂), zmienia się temperatura i ciśnienie.

Prawo Charlesa

W stałej objętości ciśnienie danej masy gazu doskonałego jest wprost proporcjonalne do jego temperatury bezwzględnej tzn.:

lub

ciśnienie gazu w temp 273K

p V₂<V₁

V₁

T

Półprosta przedstawiająca zależności ciśnienia gazu od temperatury w stałej objętości nazywa się izochor. W przemianie izochorycznej praca nie jest wykonywana (stała objętość), więc zmiana energii wew. odbywa się wyłącznie przez wymianę ciepła.

-izochoryczne ogrzewanie prowadzi do wzrostu energii wew.

-izochoryczne oziębienie obniża energię wew.

3. Przemiana adiabatyczna

Jest to taka przemiana podczas której nie następuje przemiana wymiana ciepła z otoczeniem a więc kiedy przemiana zachodzi bardzo szybko lub kiedy gaz jest odizolowany cieplnie od otoczenia.

,

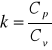
p

adiabata

Ciśnienie wzrasta szybciej w przemianie adiabatycznej niż w izotermicznej

izoterma

T

W przemianie adiabatycznej zmiana energii wewnętrznej odbywa się wyłącznie przez pracę

Q=const.

-dla adiabatycznego sprężania (energia wew. rośnie)

ΔEw=W

-dla adiabatycznego rozprężania (energia wew. maleje)

ΔEw=-W

Podstawowy wzór teorii kinetyczno molekularnej gazów.

Ciśnienie wywierane przez gaz na ścianki naczynia jest wprost proporcjonalne doliczby częsteczek w jednostce objętości i do ich średniej energii kinetycznej

lub

Ciepło molowe gazu.

Ciepłem mollowym substancji nazywamy ilość ciepła potrzebną do ogrzania 1 mola tej substancji o 1K

Ciepło molowe w przemianie izobarycznej (C_p) i izochorycznej (C_h)

Podczas ogrzewania gazu mogą ulegać zmianie wszystkie jego parametry, można go również ogrzewać przy stałej objętości (przemiana izochoryczna) lub pod stałym ciśnieniem (przemiana izobaryczna).

W każdym z tych przypadków 1 mol gazu ogrzewając o 1K pobierze określoną ilość energii.

C_p>C_v

Ciepło molowe w przemianie izobarycznej (C_p) jest większe niż w przemianie izochorycznej (C_v), ponieważ przy ogrzewaniu gazu w stałej objętości całe dostarczone ciepło zużywane jest wyłącznie na podniesienie jego temperatury, natomiast w stałym ciśnieniu część dostarczanego ciepła jest zużyta na wykonanie pracy czyli podniesienie tłoka w celu zachowania stałego ciśnienia i tylko część na podwyższenie temperatury. Dla gazu doskonałego zachodzi zależność:

C_p-C_v=R, R- stała gazowa (8,31
)

2) CZEŚĆ DOŚWIADCZALNA

Lp.	h1 [mm]	h2 [mm]	h1-h2 [mm]	[mm]
1.	16,5	3,5	13	1,26
2.	16	3,5	12,5	1,28
3.	16,5	4	12,5	1,32
4.	18	4,5	13,5	1,33
5.	16	3	13	1,23
6.	14	2,5	11,5	1,21
7.	15	3	12	1,25
8.	17	3,5	13,5	1,25
9.	16	3	13	1,23
10.	16	3,5	12,5	1,28

Obliczam średnią arytmetyczną ℵ:

(1,26+1,28+1,32+1,33+1,23+1,21+1,25+1,25+1,23+1,28)=1,271

Obliczam błąd pomiaru metodą Studenta Fishera

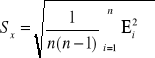
= 1,271-1,26=0,0011

0,000121+0,000081+0,002401+0,003481+0,001681+0,003721+0,000441+0,000441

+0,001681+0,000081=0,01413

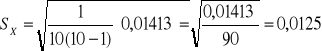
ℵ=1,271
0,012 =[1,259:1,283]

Wnioski:

Ćwiczenie mające na celu wyznaczenie ℵmetodą Clemanta- Desormesa w pełni odzwierciedla zamierzony cel.

Błąd pomiaru ℵ=1,271+-0,012 nie jest duży a jego przyczyną mogą być złe odczytanie wyniku oraz niedokładne przyrządy.

1

---