Pytanie 1

Prawa de Morgana dla zmiennych

Zaprzeczenie implikacji

Prawo kontr pozycji

Pytanie 2

Prawa de Morgana dla Kwantyfikatorów

Prawa przestawiania kwantyfikatorów

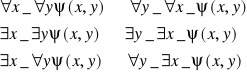
Pytanie 3

Działania na zbiorach

Niech
Możemy zdefiniować następujące

działania na zbiorach

Suma zbiorów A i B

Iloczyn (część wspólna) zbiorów A i B

Różnica zbiorów A i B

Dopełnienie zbioru A do X

Jeśli dane są zbiory nie puste A i B to można

utworzyć zbiór, który oznaczamy
złożony

ze wszystkich par uporządkowanych
, gdzie

i
. Zbiór ten nazywamy iloczynem (produktem) kartezjańskim zbiorów A i B.

Pytanie 4

Definicja kresu dolnego i górnego, twierdzenie o istnieniu kresów:

1) Mówimy, że zbiór A jest ograniczony z góry gdy

istnieje liczba
(zwana ograniczeniem górnym

zbioru A) taka, że:

Kresem górnym zbioru A nazywamy najmniejsze z

ograniczeń górnych zbioru A. Oznaczamy kres górny

przez symbol supA (supremum A)

2) Mówimy, że zbiór A jest ograniczony z dołu gdy

istnieje liczba
(zwana ograniczeniem dolnym

zbioru A) taka, że:

Kresem dolnym zbioru A nazywamy największe z

ograniczeń dolnych zbioru A i

oznaczamy infA (infinium A)

Twierdzenie o istnieniu kresów:

1) Każdy zbiór niepusty
ograniczony z

góry posiada dokładnie jeden kres górny

2) Każdy zbiór niepusty
ograniczony z

dołu posiada dokładnie jeden kres dolny

Pytanie 5

Wartość bezwzględna i jej własności:

Dla
definiujemy jej wartość bezwzględną wzorem:

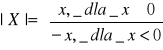
Własności:

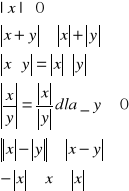
Pytanie 6

Definicja funkcji, iniekcja, suriekcja, bijekcja, funkcja odwrotna, superpozycja funkcji:

Niech
,
. Zbiór
nazywamy

funkcją, gdy dla każdego
istnieje dokładnie

jeden element
taki, że

W skrócie:

Piszemy
oraz zamiast
piszemy y = f(x)

Niech
. Mówimy, że:

a) f jest iniekcją (albo inaczej funkcją różnowartościową), gdy

(Uwaga: korzystając z prawa kontrapozycji, można powyższy warunek zapisać w postaci

b) f jest suriekcją (albo inaczej funkcją „na”), gdy

f(x) = y

c) f jest bijekcją, gdy jest jednocześnie iniekcją i suriekcją.

Pytanie 7

Zasada indukcji zupełnej:

Niech
będzie funkcją zdaniową, której dziedziną jest zbiór liczb naturalnych N. Jeśli:

1)
zachodzi

2) dla każdej liczby naturalnej u zachodzi wynikanie

to
zachodzi dla każdej liczby naturalnej u.

Pytanie 8

Definicja ciągu liczbowego, monotoniczność, ograniczoność:

Ciągiem liczbowym (nieskończonym) nazywamy każdą funkcje f określoną na zbiorze liczb naturalnych. Wartości tej funkcji nazywamy wyrazami ciągu i oznaczamy
a ciąg o wyrazach
zapisujemy symbolem (
) lub a₁, a₂, a₃...

Monotoniczność: Mówimy, że ciąg
jest:

1) niemalejący gdy

rosnący gdy

2) nierosnący gdy

malejący gdy

Jeśli ciąg jest niemalejący lub nierosnący to nazywa się monotonicznym.

Ograniczoność: Ciąg
nazywa się ograniczonym jeśli zbiór jego wyrazów
jest zbiorem ograniczonym w zbiorze liczb rzeczywistych. Oznacza to, że
(*)

Warunek (*) można zastąpić przez:

Pytanie 9

Ciągi zbieżne i ich własności:

Ciąg nazywamy zbieżnym, gdy ma granicę (gdy istnieje liczba g taka że granica
). Gdy taka liczba nie istnieje to ciąg nazywa się rozbieżnym.

Własności:

1) Jeśli ciąg
jest zbieżny, to ma dokładnie jedną granicę.

2) Jeśli ciąg
jest zbieżny, to jest ograniczony.

Z tego wynika:

a)

b)

Jeśli
i
gdzie
to

1)

2)

3)

Pytanie 10

Twierdzenie o trzech ciągach:

Jeśli

oraz
, to

Dowód: Niech ε > 0. Z założenia mamy

Koniunkcja nierówności
implikuje

I z założenia

Skąd mamy

zatem

Co daje tezę.

Uwaga: Twierdzenie pozostaje prawdziwe, jeśli zakładać, że
dla prawie wszystkich

Pytanie 11

Twierdzenie o zbieżności ciągów monotonicznych. Liczba e:

Twierdzenie o zbieżności ciągów monotonicznych - Jeśli ciąg
jest od pewnego miejsca monotoniczny i jednocześnie ograniczony to jest zbieżny.

Liczbą e - nazywamy granicę ciągu
,
. Liczba ta jest równa 2,7182818284

Pytanie 13

Ciągi rozbieżne do
:

a) Ciąg
nazywamy rozbieżnym do
gdy
. Piszemy:

b) Ciąg
nazywamy rozbieżnym do

gdy
. Piszemy:

Pytanie 13

Granice częściowe ciągów, granica dolna i górna:

Granicą częściowa ciągu
nazywamy element
taki, że
=g dla pewnego podciągu
ciągu (
)

a) Granicą dolną ciągu (
) nazywamy kres inf
i oznaczamy przez
lub lim

b) Granicą górną ciągu (
) nazywamy kres sup
i oznaczamy przez
lub lim

Pytanie 14

Funkcje elementarne i ich rodzaje:

Podstawowymi funkcjami elementarnymi są: wielomiany, funkcje wymierne, funkcje potęgowe, funkcje wykładnicze, funkcje logarytmiczne, funkcje trygonometryczne oraz funkcje cyklometryczne (odwrotne do trygonometrycznych).

Funkcja elementarna powstaje przez zastosowanie skończoną ilość razy podstawowych funkcji elementarnych, działań arytmetycznych (dodawane, odejmowanie, mnożenie i dzielenie) oraz operacji superpozycji, pod warunkiem, że zastosowane operacje mają sens.

Pytanie 15

Definicja Cauchy'ego granicy funkcji w punkcie:

Niech
. Wówczas

Pytanie 17

Własności algebraiczne granic funkcji w punkcie:

Niech
;
;
;
- punkt skupienia zbioru E. Załóżmy, że istnieją skończone granice:
i
. Wtedy

1)

2)

3)

4)
o ile
dla
oraz

Pytanie 18

Definicja ciągłości funkcji w punkcie i na zbiorze:

Niech
,
,

Mówimy, że funkcja f jest ciągła w punkcie
gdy:

1)
nie jest punktem skupienia zbioru E

2)
jest punktem skupienia zbioru E oraz

Funkcja
nazywa się ciągłą na zbiorze E gdy jest ciągła w każdym punkcie tego zbioru.

Pytanie 19

Rodzaje nieciągłości funkcji w punkcie:

Rozróżniamy następujące typy nieciągłości funkcji f w punkcie
przy założeniu, że f jest określona w otoczeniu obustronnym punktu
:

1) Istnieją obie granice jednostronne skończone, a więc granica lewostronna w punkcie

i
i są równe, ale obie różne od f(
) (nieciągłość I rodzaju - nieusuwalna)

1a) Istnieją obie granice jednostronne skończone w punkcie
ale są różne (nieciągłość I rodzaju - nieusuwalne)

2) Przynajmniej jedna z granic jednostronnych nie istnieje lub jest nieskończona (nieciągłość II rodzaju)

Pytanie 20

Własności funkcji ciągłych na przedziale:

Twierdzenie Weierstrassa: Jeśli
jest funkcją ciągłą na [a,b], to f jest ograniczona oraz f osiąga swoje kresy, tzn. istnieją takie liczby
, że:

Twierdzenie Darboux: Jeśli f jest funkcją ciągłą na pewnym przedziale I, to dla dowolnych liczb
i dla dowolnej liczby y leżącej między f(a) i f(b) istnieje liczba c leżąca między a i b, taka że y = f(c)

Pytanie 21

Iloraz różnicowy, pochodna funkcji w punkcie:

Niech
gdzie
, oraz niech

Funkcję
daną wzorem

,

Nazywamy ilorazem różnicowym funkcji f w punkcie x. Liczba h = t - x oznacza przyrost argumentu, zaś liczba f(t) - f(x) jest odpowiednim przyrostem funkcji.

Pochodna: Granicę
, jeśli istnieje, nazywamy pochodną funkcji f w punkcie
i oznaczamy f'(
). Jeśli f'(
) istnieje i jest skończona to mówimy, że f jest różniczkowalna w punkcie

Pytanie 22

Warunek konieczny różniczkowalności:

Jeśli funkcja
jest różniczkowalna w punkcie
to jest ciągła w punkcie

Dowód - Mamy:

. Stąd
tzn. f jest ciągła w

Pytanie 23

Własności algebraiczne pochodnych:

Załóżmy, że f i g mają skończone pochodne w punkcie x. Wtedy:

1)

2)

3)

Pytanie 24

Twierdzenie o pochodnej funkcji odwrotnej, pochodna superpozycji:

Twierdzenie o pochodnej funkcji odwrotnej. Jeśli
jest ciągłą iniekcją, różniczkowalną w punkcie
oraz
to funkcja odwrotna
jest różniczkowalna w punkcie
oraz

Różniczkowanie superpozycji Niech będą dane funkcje
oraz
, przy czym
. Załóżmy, że funkcja f jest różniczkowalna w punkcie
, zaś funkcja g - różniczkowalna w punkcie
. Wówczas funkcja
jest różniczkowalna w punkcie x oraz

Pytanie 25

Interpretacja geometryczna i fizyczna pochodnej:

Interpretacja geometryczna: Niech
,

Czym jest

Prosta PQ nazywa się sieczną. Jej współczynnik kierunkowy jest równy

Interpretacja fizyczna:

1) Prędkość chwilowa: t - czas, s(t) - przebyta droga

ustalmy chwilę
,
- przyrost czasu

Iloraz
- prędkość średnia w czasie od
do
= t

- prędkość chwilowa w chwili
(V(
))

2) Przyśpieszenie chwilowe: V(t) - prędkość chwilowa w chwili t

Ustalmy

- przyśpieszenie średnie w czasie od
do t

- przyśpieszenie chwilowe w chwili
(a(
))

3) Natężenie prądu: q(t) - ładunek elektryczny, jaki przepłynął przez dany przekrój przewodu od chwili
do
= t

- średnie natężenie prądu od
do t

- natężenie prądu w chwili

Pytanie 26

Definicja różniczki:

Niech funkcja f będzie różniczkowalna w punkcie
. Różniczką funkcji f w punkcie
nazywamy funkcję liniową, która dowolnej liczbie rzeczywistej
przypisuje liczbę
. Różniczkę funkcji f w punkcie
będziemy oznaczać jako
.

Pytanie 27

Minima i maksima Lokalne Twierdzenie Fermata

Niech
gdzie X jest przestrzenią metryczną. Mówimy, że funkcja f ma w punkcie
maksimum (odpowiednio minimum) lokalne, gdy

Jeśli odpowiednio w powyższym warunku nierówność
(odpowiednio
) zastąpić przez < (odpowiednio >) , to mówimy o maksimum (odpowiednio minimum) lokalnym właściwym. Minimum lub maksimum lokalne funkcji nazywa się ekstremum lokalnym

Twierdzenie Fermata Jeśli
funkcja ma w punkcie
ekstremum lokalne oraz pochodna
istnieje, to

Pytanie 28

Twierdzenia o wartości średniej:

Rolle'a:

Jeśli
jest funkcją ciągłą na [a,b] i różniczkowalną na (a,b) oraz f(a)=f(b) , to istnieje punkt
taki, że

Cauchy'ego:

Jeśli
są funkcjami ciągłymi na [a,b] i różniczkowalnymi na (a,b), to istnieje taki punkt
, że

Lagrange'a:

Jeśli
jest funkcją ciągłą na [a,b] i różniczkowalną na (a,b) to istnieje punkt
taki, że

Pytanie 29

Wnioski z tw. Lagrange'a:

Załóżmy ze funkcja
jest różniczkowalna na (a,b)

Jeśli
dla każdego
, to funkcja f jest stała na (a,b)

Jeśli
(odpowiednio
), to funkcja f jest niemalejąca (odpow. rosnąca) na (a,b)

Jeśli
(odpowiednio
), to funkcja f jest nierosnąca (odpow. malejąca) na (a,b)

Pytanie 30

Asymptoty:

Niech
,
,
. Jeśli
(odpowiednio.
) to mówimy, że prosta x=x₀ jest prawostronną( odpowiednio lewostronną) asymptotą pionową wykresu funkcji f.

Załóżmy, że funkcja rzeczywista f jest określona w przedziale postaci

(odpowiednio
), gdzie
. Mówimy, że prosta y=ax+b jest asymptotą wykresu funkcji f
(odpowiednio w
), gdy

odpowiednio

Twierdzenie o asymptotach. Prosta y=ax+b jest asymptotą ukośną wykresu funkcji f w
wtedy i tylko wtedy, gdy
oraz

(odpowiednio w
)

Pytanie 31

Niech
. Załóżmy, że funkcje
są różniczkowalne na (a,b), przy czym g'(x)><0 dla każdego
oraz istnieje granica

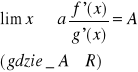
jeśli ponadto

to

Analogiczne twierdzenie zachodzi gdy
w w/w równościach

Pytanie 32

Funkcje wypukłe i wklęsłe, punkty przegięcia, związek z drugą pochodna:

Mówimy że funkcja f jest wypukła ( odpowiednio ściśle wypukła) na I gdy dla dowolnych punktów
takich, że
i dowolnego punktu
mamy
(odpowiednio
) ), gdzie
jest funkcją, której wykres jest prostą przechodzącą przez punkty
,
> Stosując równanie prostej przechodzącej przez dane dwa punkty

wypukłość (odpowiednio ścisłą wypukłą funkcji f na I można zapisać jako

Odpowiednio

Jeśli w definicji zastąpić nierówność
(odpow. <) przez
(odpow. >), to mówimy, że funkcja f jest wklęsła (odpow. ściśle wklęsła) na I

Pytanie 33

Niech
oraz
. Załóżmy, że n-ta pochodna f⁽ⁿ⁾ funkcji f istnieje i jest ciągła na [a,b], zaś pochodna f⁽ⁿ⁺¹⁾ istnieje wszędzie na (a,b). Niech
. Określamy wielomian P wzorem

Wtedy dla każdego
,każdego
, istnieje
leżący między x i x₀ taki, że

Pytanie 34

Funkcja Pierwotna, całka nieoznaczona własności:

Mówimy, że funkcja różniczkowalna
jest funkcją pierwotną funkcji
, gdy F'(x)=f(x) dla każdego I.

Załóżmy, że F₀ jest ustaloną funkcją pierwotną funkcji
. Funkcja
jest funkcją pierwotną funkcji f wtedy i tylko wtedy, gdy istnieje stałą
taka, że F(x)= F₀(x)+C dla każdego

Jeśli funkcja
posiada przynajmniej jedną funkcję pierwotną
, to ogólną postać F(x)+C,

(gdzie C
R) funkcji pierwotnej funkcji f nazywamy całką nieoznaczoną funkcji f i oznaczamy przez
albo
. Zatem
albo krótko
, gdzie C jest dowolną stałą.

Liniowość całki nieoznaczonej Załóżmy, że
oraz istnieją całki
i
. Wtedy istnieje całka
oraz

; dla dowolnej liczby
istnieje całka
oraz

Pytanie 40

Definicja (całki oznaczonej Riemanna):

Niech f będzie funkcją ograniczoną na przedziale [a,b] i niech zbiór P_n={x₀, x₁,…, x_n} oznacza podział odcinka [a,b] na n części, przy czym a= x₀< x₁<…< x_n=b. Niech

x_k=x_k-x_k-1 oznacza długość k-tego odcinka podziału P_n, gdzie 1kn oraz δ(P_n)=max{x_k: 1kn} oznacza średnicę podziału P_n, zaś x_k^*[ x_k-1, x_k] oznacza punkt pośredni k-tego odcinka podziału P_n, gdzie 1kn.

Sumą całkową funkcji f na przedziale [a,b] odpowiadającą podziałowi P_n oraz punktom pośrednim x_k^* tego podziału gdzie 1kn, nazywamy liczbę

.

Całkę oznaczoną Riemanna z funkcji f na przedziale [a,b] definiujemy wzorem;

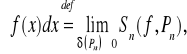
o ile istnieje granica właściwa występująca po prawej stronie znaku równości oraz granica ta nie zależy od sposobu podziałów P_n przedziału [a,b] ani od sposobu wyboru punktów pośrednich x_k^*, gdzie 1kn. Ponadto przyjmujemy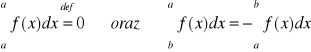
dla a<b.

Funkcję, dla której istnieje całka oznaczona Riemanna na [a,b] nazywamy funkcją całkowalną na [a,b].

Pytanie 42

Własności całko oznaczonej

Liniowość całki:

Niech
oraz
Jeśli
na [a,b] to
na [a,b] oraz

Jeśli
na [a,b] to
na [a,b] oraz

Monotoniczność całki:

Jeśli funkcje rzeczywiste f i g są całkowalne w sensie Riemanna na [a,b] oraz
dla każdego
, to

Niech

Jeśli
na [a,b], to
na [a,b], oraz

Jeśli
na [a,b], to
na [a,b].

Pytanie 43

Twierdzenie Riemanna:

Każda Funkcja ciągła na
jest całkowalna w sensie Riemanna

Dowód. Niech
. Funkcja f jako ciągła na zbiorze zwartym [a,b] jest jednostajnie ciągła. Zatem

Niech
będzie takim podziałem przedziału [a,b], że
Ponieważ funkcja ciągła na zbiorze zwartym osiąga swoje kresy, więc
oraz

dla pewnych punktów
;

i=1,2,....,n. Zatem

<

Stąd wynika teza.

Pytanie 44

Twierdzenie o górnej granicy całkowania: Niech
na [a,b]. Określmy funkcje górnej granicy całkowania wzorem

dla
.

Funkcja F spełnia warunek Lipschitza na [a,b] (zatem jest jednostajnie ciągła na [a,b]).

Jeśli funkcja F jest ciągła w punkcie
, to funkcja F jest różniczkowalna w x₀ oraz F'(x₀)=f(x₀).

Pytanie 45

Wzór Newton-Liebnetz'a:

Jeśli
na [a,b], oraz F jest funkcją pierwotną funkcji f na [a,b] to

Dowód. w/w równość będzie wykazana, jeśli udowodnimy, że

Niech więc
. Ponieważ
na [a,b], więc z twierdzenie Riemanna wynika, że istnieje podział
taki, że dla dowolnego układu punktów pośrednich
(i=1,...,n) mamy
Stosując twierdzenie Lagrange'a (korzystając z wniosków) do funkcji F na przedziale
otrzymujemy

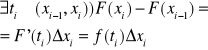
Stąd

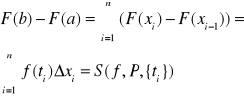
Pytanie 46

Twierdzenie o Całkowaniu przez części: Załóżmy, że funkcje
mają ciągłe pochodne na [a,b]. Wówczas

Twierdzenie o zamianie zmiennych. Załóżmy, że funkcja
będzie funkcją ciągłą. Wtedy dla dowolnych punktów
zachodzi wzór

Pytanie 47

Twierdzenie o wartości średniej dla całek:

Załóżmy, że
jest funkcją ciągłą, zaś funkcja g jest całkowalna w sensie Riemanna na [a,b] oraz nieujemna na [a,b] lun niedodatnia na [a,b]. Wówczas

Pytanie 48

Długość łuku krzywej:

Jeżeli łuk l dany jest równaniami parametrycznymi:

przy czym nie ma punktów wielokrotnych oraz funkcje x i y posiadają ciągłe pochodne na przedziale [,], to długość l łuku l wyraża się wzorem:

.

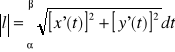
Jeżeli łuk l dany jest równaniem jawnym
, gdzie f jest funkcją posiadającą ciągłą pochodną na przedziale [a,b], wówczas długość l tego łuku wyraża się wzorem:

.

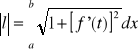
Jeżeli łuk l dany jest równaniem biegunowym
, gdzie g jest funkcją nieujemną posiadającą ciągłą pochodną na przedziale
, wówczas długość l łuku l wyraża się wzorem:

.

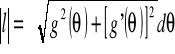
Pytanie 49

Pole powierzchni bryły obrotowej:

Niech krzywa AB będzie dana równaniem
, gdzie f jest funkcją nieujemną posiadającą ciągłą pochodną na przedziale [a,b]. Wówczas pole powierzchni S powstałej w wyniku obrotu krzywej AB dokoła osi Ox wyraża się wzorem:

.

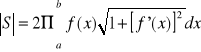
Niech krzywa AB będzie dana równaniami parametrycznymi:

gdzie funkcje x i y posiadają ciągłe pochodne i y jest nieujemna na przedziale
, oraz krzywa AB nie posiada punktów wielokrotnych. Wówczas pole powierzchni S powstałej w wyniku obrotu krzywej AB wokół osi Ox wyraża się wzorem:

.

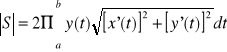
Objętość bryły obrotowej:

Niech S(x), gdzie x∈[a.b], oznacza pole przekroju bryły V płaszczyzną prostopadłą do osi OX w przestrzeni X oraz niech S będzie funkcją ciągłą na przedziale [a,b]. Wtedy objętość bryły V wyraża się wzorem;

.

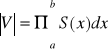
Niech
, gdzie f jest funkcją ciągłą na przedziale [a,b], oznacza trapez krzywoliniowy. Wtedy objętość bryły V powstałej z obrotu trapezu krzywoliniowego D wokół osi 0x wyraża się wzorem:

.

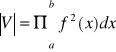
Pytanie 50

Zbieżność całki niewłaściwej:

Niech
oraz załóżmy, że funkcja f jest całkowalna w sensie Riemanna na każdym przedziale
. Mówimy, że b jest punktem osobliwym funkcji f, gdy zachodzi jeden z dwóch przypadków:

1

2 funkcja jest nieograniczona na każdym przedziale
Całką niewłaściwą funkcji f na [a,b) nazywamy granice
( o ile ta granica istnieje) oraz oznaczamy ją przez
. Jeśli granica ta jest skończona, to mówimy, że całka
jest zbieżna, jeśli zaś nie istnieje lub jest nieskończona to mówimy, że całka
jest rozbieżna. Ponadto mówimy, że całka
jest bezwzględnie zbieżna, gdy całka
jest zbieżna.

Pytanie 52

Definicja szeregu:

Niech
będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg
gdzie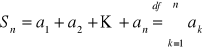
. Taki szereg liczbowy oznaczamy symbolem
. Liczbę
nazywamy n-tym wyrazem, a liczbę
- n-tą sumą tego szeregu.

Pytanie 53

Warunek konieczny zbieżności szeregu: Jeśli szereg
jest zbieżny to

Dowód Niech s_n oznacza n-tą sumę częściową szeregu
. Stąd

Pytanie 55

Kryterium porównawcze:

Jeśli
to ze zbieżności szeregu
wynika zbieżność szeregu
i z rozbieżności szeregu
wynika rozbieżność szeregu
.

Pytanie 56

Kryterium Cauchy'ego:

Jeśli
to
jest zbieżny gdy
i rozbieżny gdy
.

Kryterium d'Alemberta:

Jeśli
oraz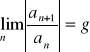
to szereg
jest zbieżny gdy
i rozbieżny gdy
.

Pytanie 57

Kryterium Leibniza:

Jeśli
jest ciągiem nierosnącym zbieżnym do 0, to szereg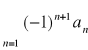
zwany szeregiem naprzemiennym jest zbieżny.

Pytanie 58

Definicja ciągu funkcyjnego:

Przyjmijmy, że
.

Ciągiem funkcyjnym określonym na zbiorze
nazywamy każdą funkcję odwzorowującą zbiór
w zbiór
. Załóżmy, że
. Wówczas dla oznaczenia ciągu funkcyjnego, którego n-tym wyrazem jest funkcja
używamy oznaczenie
.

Niech
oznacza ciąg funkcyjny taki, że
. Niech
.

Niech
będzie ciągiem funkcyjnym takim, że
. Szeregiem funkcyjnym nazywamy ciąg funkcyjny
gdzie
. Taki szereg funkcyjny oznaczamy symbolem
. Funkcję
nazywamy n-tym wyrazem a funkcję
nazywamy n-tą sumą tego szeregu.

Pytanie 59

Definicja zbieżności punktowej ciągu funkcyjnego:

Mówimy, że ciąg
jest punktowo zbieżny na zbiorze
do funkcji
jeśli
.

Definicja zbieżności jednostajnej ciągu funkcyjnego

Mówimy, że ciąg
jest jednostajnie zbieżny na zbiorze
do funkcji
jeśli
.

Fakt, że
jest punktowo zbieżny do funkcji
na zbiorze
oznaczamy pisząc
.

Fakt, że
jest jednostajnie zbieżny do funkcji
na zbiorze
oznaczamy pisząc


.

---