Pola magnetyczne wytworzone przez prąd elektryczny

1. Prawo Biota-Savarta

2. Pole magnetyczne wytworzone przez długi, prosty przewód z prądem

3. Zastosowania prawa Biota-Savarta

4. Dwa równoległe przewodniki przewodzące prąd

5. Prawo Ampera

6. Solenoidy i toroidy

***********************************************************************************

1. Prawo Biota-Savarta

Nasz cel = obliczyć indukcję magnetyczą B wytworzoną przez rozkład prądów.

⇒ Przypomnijmy procedurę obliczania pola E wytworzonego przez dany rozkład ładunków:

⇒
(1)

r - odległość od ładunku dq do punktu P; dla (+)dq kierunek

(wektor rozciągnięty pomiędzy dq a P). Używając,
możemy ponownie zapisać Równ. (1) w postaci wektorowej:

(2)

** Wyznaczenie pola B jest nieco większym wyzwaniem niż wyznaczenie pola E!

Aby obliczyć pole magnetyczne w pobliżu punktu P pochodzące od prądu (stałego) w przewodzie, o dowolnym kształcie, przenoszącym prąd o natężeniu i:

• Podziel przewód na różniczkowe składowe ds

• Zdefiniuj różniczkowy element
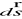
  : styczny do przewodu, w kierunku i, długość ds

• Zdefiniuj różniczkowy element prądowo-odległościowy (i
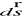
  ) wytwarza on w punkcie P pole magnetyczne o indukcji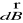
  o wielkości dB (skierowane ⊥ `do' kartki):

(3)

μ_o = stała przenikalności magnetycznej:

μ_o = 4π×10⁻⁷ T•m/A ≈ 1.26×10⁻⁶ T•m/A

θ - kąt pomiędzy kierunkami
,

= wektor rozciągnięty od ds do P.

Rów. (3): skalarna forma prawa Biota-Savarta

Prawo to zostało wywnioskowane eksperymentalnie.

Wzór Biota - Savarta umożliwia obliczenie indukcji magnetycznej gdy znane jest natężenie prądu, który jest źródłem pola magnetycznego (punkty tego pola są scharakteryzowane przez wektor indukcji, a wartość tego wektora określa wzór Biota - Savarta). (Wikipedia)

• 
  Oblicz wypadkową indukcję B w punkcie P przez sumowanie (całkowanie) wkładów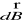
  od elementów prądowo-odległościowych w postaci wektorowej:

(4)

⇒ Kierunek
⊥ `do' kartki jest wynikiem iloczynu wektorowego
.

• Prawo to może być wykorzystane do obliczenia wypadkowego pola magnetycznego wytworzonego w danym punkcie przez różnorodny rozkład prądu elektrycznego.

2. Pole magnetyczne wytworzone przez długi, prosty przewód z prądem

3. Zastosowania prawa Biota-Savarta

Rów. (3) daje wielkość indukcji pola B wytworzonej przez pojedynczy element prądowo -odległościowy. Aby wyznaczyć wypadkowe B wytworzone w danym punkcie przez prąd w zakrzywionym przewodzie:

⇒ należy scałkować po wszystkich składowych prądowo-odległościowych.

Całkowanie może być trudne, zależnie od kształtu przewodu ⇒ proste przykłady:

(1) Kołowy łuk przewodu & punkt który jest centrum krzywizny:

Rozważamy niewielką część łuku ds:

Z rów. (3) - pole B wytworzone przez prąd o natężeniu i w kołowym łuku przewodu:

⇒

⇒
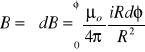
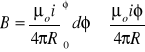
[B w centrum kołowego łuku; φ musi być w radianach]

(2) Kołowa pętla prądowa & punkt znajdujący się w jej centrum:

Wielkość pola magnetycznego w centrum przewodu w postaci pełnego okręgu, tj. kołowej pętli prądowej ⇒ podstawić 2π radianów za φ w powyższym równaniu:

⇒
(6) [B w centrum pełnego okręgu z prądem]

U1: Ogólne zastosowania rów. (4) [= prawo Biota-Savarta w postaci wektorowej] mogą zostać uproszczone przez obliczenie B oddzielnie dla:

(1) prostych części i (2) kołowych łuków przewodu.

(3) Kołowa pętla prądowa - punkt P na osi okręgu:

Dodając wkład od wszystkich części, pole magnetyczne wytworzone przez kołową pętlę prądową w punkcie (z) na jej osi centralnej wynosi:

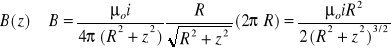
. (7)

(4) Zwój przewodzący prąd jako dipol magnetyczny:

Poprzednio rozważaliśmy moment obrotowy działający na ramkę z prądem i wykryliśmy, że zwój przewodzący prąd elektryczny jest równoważny dipolowi magnetycznemu.

W przybliżeniu z >> R, tj. dla punktów osiowych położonych z dala od pętli, rów. (7) redukuje się do: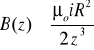

Dla cewki o N zwojach: πR² = pole A pętli ⇒ R² = A/π & i → N i

⇒

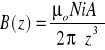
Wykorzystując definicję dipolowego magnetycznego momentu cewki: μ = N i A,

i ponieważ kierunek indukcji pola magnetycznego B jest identyczny jak kierunek dipolowego momentu magnetycznego pętli: μ (także wektor), w postaci wektorowej:

⇒
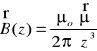
(8)

Stąd, cewka przewodząca prąd może być uznana jako dipol magnetyczny:

(1) Jeśli umieścimy ją w zewnętrznym polu magnetycznym, doświadcza ona działania momentu obrotowego.

(2) Wytwarza ona swoje własne wewnętrzne pole magnetyczne - dla odległych punktów położonych na jej osi opisane przez rów. (8).

Pętla z prądem wytwarza pole magnetyczne identyczne jak magnes sztabkowy i w podobny sposób można jej przypisać bieguny północny i południowy. Dipolowy moment magnetyczny pętli μ, wyznaczony przez regułę prawej dłoni, wskazuje kierunek od południowego (S = South) bieguna do północnego (N = North), w kierunku indukcji B wewnątrz pętli.

4. Dwa równoległe przewodniki przenoszące prąd

Rozważamy dwa bardzo długie proste przewody: `a', `b' przewodzące prąd: i_a, i_b. Przewód `a' wytwarza pole magnetyczne o indukcji B<sub>a</sub>, które działa siłą magnetyczną F<sub>ba</sub> na przewód `b' (i odwrotnie!).

Z rów. (5) na pole B pochodzące od nieskończenie długiego przewodu z prądem:

⇒

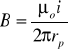
Z równania na siłę magnetyczną działającą na przewód z prądem:

⇒

⇒

⇒ Dwa bardzo długie przewody z prądem o

natężeniu 1 A, oddalone o 1 metr znajdujace

się w próżni przyciągają się wzajemnie

z siłą 2 × 10⁻⁷ N na metr.

⇒ Inna defnicja jednostki: [Amper]

5. Prawo Ampera (wytworzenie pola magnetycznego przez prąd elektr.)

Przypomnienie: aby wyznaczyć wypadkowe pole E od dowolnego rozkładu ładunków:

⇒ należy użyć prawa odwrotności kwadratu dla różniczkowego pola
w rów. (2) (jeśli rozkład jest skomplikowany należy użyć komputera);

⇒ Jeżeli rozkład jest planarnie, cylindrycznie lub sferycznie symetryczny łatwiej jest zastosować prawo Gaussa do wyznaczania wypadkowego pola.

Podobnie: aby wyznaczyć wypadkową indukcję B od dowolnego rozkładu ładunków:

⇒ należy użyć prawa odwrotności kwadratu dla różniczkowego pola
w rów. (4) (jeśli rozkład jest skomplikowany należy użyć komputera);

⇒ jeśli rozkład charakteryzuje się jakąś symetrią łatwiej jest użyć prawa Ampera aby wyznaczyć wartość indukcji .

Podstawowa idea: prawo Gaussa:
; prawo Ampera:

Prawo Ampera można wyprowadzić z prawa Biota-Savarta w ogólnej formie:

Kółeczko (o) na znaku całki oznacza, że iloczyn skalarny jest scałkowany po pętli zamkniętej, nazwanej pętlą amperowską. Natężenie prądu i_enc po prawej stronie oznacza wypadkowy prąd otoczony (ang. encircled) tą pętlą.

Znaczenie: Bierzemy dowolną zamkniętą pętlę w przestrzeni, obliczamy całkę liniową:
jej wartość jest równa μ_oi, gdzie i jest to natężenie prądu zamkniętego wewnątrz pętli.

Prosty przykład: nieskończenie długi, prosty przewód przewodzący prąd:

⇒
; r = odległość mierzona w kierunku ⊥ do przewodu Wynik jak w rów. (5)!

6. Solenoidy i toroidy

Rozważmy: pole magnetyczne wytworzone przez prąd płynący w solenoidzie (lewy rys.), tj. długa, ciasno nawinięta spiralna zwojnica z przewodu (drutu).

Rys. L: Pionowy przekrój poprzeczny wzdłuż osi głównej “wydłużonego” solenoidu. Pokazane są linie pola magnetycznego pochodzącego od prądu płynącego przez solenoid. Każdy zwój wytwarza okrężne linie pola w swoim pobliżu. W pobliżu osi solenoidu, linie pola łączą się w wypadkowe pole magnetyczne skierowane wzdłuż osi. Ciasno upakowane linie pola oznaczają silne pole magnetyczne. Na zewnątrz solenoidu linie pola są upakowane dużo swobodniej - pole jest dużo słabsze.

Rys. P: Linie sił pola od rzeczywistego solenoidu o skończonej długości.

Pole jest silne i jednorodne w punktach wewnętrznych, takich jak P1, a relatywnie słabe w punktach na zewnątrz, np. P2.

Zastosowanie prawa Ampera: [wyprowadzenie „dodatkowo”]

pojedynczy segment długiego, idealnego solenoidu, przenoszący prąd o natężeniu i

⇒ przyjmij pętlę amperowską jako prostokąt abcd. [zob. rys. poniżej]

U1: Dla idealnego solenoidu: B jest jednorodne wewnątrz solenoidu i zerowe na zewnątrz.

LSR:
≡ ∑ po każdej pętli ⇒ suma czterech całek:

a-b całka = Bh ; B - wielkość indukcji jednorodnego pola wewnątrz;

h - (dowolna) długość segmentu od a do b.

b-c & d-a całki = zero ; ponieważ dla każdego elementu ds tych segmentów:

jest prostopadłe do
lub równe zero ⇒ iloczyn skalarny wynosi zero.

c-d całka = zero ; ponieważ B = 0 we wszystkich punktach zewnętrznych.

⇒ suma czterech całek (po całej prostokątnej pętli) = Bh.

PSR: jeśli uzwojenie solenoidu przechodzi przez tą pętlę więcej niż jeden raz

⇒ wypadkowe natężenie prądu i_enc otoczonego tą prostokątną pętlą amperowską (z ang. enc = encircled;zob. rys. powyżej) jest inne niż natężenie prądu i w uzwojeniach.

Oznaczenia: l - długość solenoidu, N - ilość zwojów,

n - liczba zwojów na jednostkę długości solenoidu:

⇒ Pętla zamyka nh zwojów ⇒ i_enc = i nh

⇒ Prawo Ampera daje wtedy: Bh = μ₀ i_enc = μ₀ i nh

⇒ Pole magnetyczne wewnątrz nieskończenie długiego, idealnego solenoidu:

lub

U2: Równanie to sprawdza się całkiem dobrze w rzeczywistych solenoidach jeśli zastosujemy je wyłącznie w punktach wewnątrz solenoidu, oddalonych znacznie od obu jego końców.

U3: Jest to zgodne z eksperymentem:

(i) wielkość B wewnątrz solenoidu nie zależy ani od średnicy, ani od długości solenoidu oraz

(ii) B jest jednorodne wzdłuż przekroju solenoidu.

U4: Solenoid dostarcza jednorodne pola magnetycznego B dla przeprowadzania doświadczeń, tak jak kondensator płaski dostarcza jednorodne pola E

Przykładowy problem 30-4: Solenoid ma długość L = 1.23 m, wewnętrzną średnicę d = 3.55 cm, i przewodzi prąd o natężeniu i = 5.57 A. Składa się on z pięciu ciasno upakowanych warstw, każda 850 zwojów na długości L. Jaka jest indukcja B w jego środku?

Rozwiązanie - Kluczowe idee: (1) B ∝ (i, n), (2) B nie zależy od średnicy uzwojeń

⇒ wartość n dla pięciu identycznych warstw jest po prostu pięciokrotną wartością n dla każdej warstwy.

Odp.: użyj
, gdzie n = (5x850 zwojów)/L ⇒ B = 24.2 mT

TOROID ≡ “solenoid zagięty w zamknięty obważanek” [rys. poniżej]

(a) Toroid przewodzący prąd o natężeniu i.

(b) Poziomy przekrój toroidu.

Ćwiczenia 12

DANE:

Stała przenikalności magnetycznej: μ_o = 4π×10⁻⁷ T•m/A ≈ 1.26×10⁻⁶ T•m/A

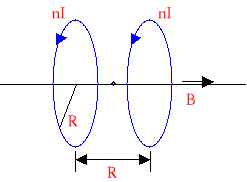
1. Para cewek Helmholtza składająca się z dwóch cewek (zob. rysunek), każda po 300 zwojów, jej promień 8.50 cm, i przewodząca prąd o natężeniu 5.00 A. Oblicz pole magnetyczne wytworzone po środku pomiędzy tymi cewkami.

(W: zwróć uwagę na przestrzeń pomiędzy cewkami i zastosuj formułę dla pola magnetycznego wytworzonego przez każdą z cewek. Przyjmij punkt odniesienia do obliczenia odległości pośrodku cewek - jak zaznaczono na rysunku, a oś cewki jako oś +x do +B.)

2. Dwa długie równoległe przewody, są oddalone o 8.0 cm. Jakie dwa identyczne prądy muszą płynąć w obydwu przewodach, jeśli indukcja pola magnetycznego w połowie odległości między nimi wynosi 300 μT? Rozważ dwa przypadki prądów płynących: (a) równolegle i (b) antyrównolegle.

3. Oblicz siłę pola magnetycznego w punkcie oddalonym o 1.00 m od długiego kabla energetycznego (300 kV) który przewodzi prąd o natężeniu 15.0 A.

(W: pole magnetyczne wytworzone przez długi przewód przewodzący prąd.)

4. Typowy solenoid z rdzeniem powietrznym w naszym laboratorium ma 1000 zwojów oraz długość 4.00 cm. Średnio promień zwoju wynosi 2.00 cm. Solenoid przewodzi prąd o maksymalnym natężeniu 10.0 A. Oblicz indukcję pola magnetycznego jakie może zostać wytworzone. Rzeczywiste pole magnetyczne może mieć indukcję nieznacznie różną, dlaczego?

(W: pole magnetyczne wytworzone przez solenoid.)

Ćwiczenia 12 - Problemy opcjonalne

5. Długi przewód przewodzący prąd o natężeniu 100 A jest umieszczony w jednorodnym zewnętrznym polu magnetycznym o indukcji 5.0 mT. Przewód jest ułożony prostopadle do tego pola. Zlokalizuj punkty w których pole magnetyczne wynosi zero.

6. Dwa długi równoległe przewody oddalone o d przenoszą prądy o natężeniu i oraz 3i płynące w tym samym kierunku. Zlokalizuj punkt lub punkty w których pola magnetyczne pochodzące od tych przewodów się znoszą (wypadkowe pole wynosi 0).

7. Solenoid o długości 1.30 m i średnicy 2.60 cm przewodzi prąd o natężeniu 18.0 A. indukcja magnetyczna wewnątrz solenoidu wynosi 23.0 mT. Wyznacz długość przewodu z którego został zrobiony ten solenoid.

Wstęp do fizyki: Wykład + ćwiczenia 12 Prof. C. Rudowicz 2012/13

11

• Gdy prąd w przewodzie płynie ⊥ `do' `do' kartki, wytworzone pole magnetyczne jest skierowane zgodnie z ruchem wskazówek zegara.

• Reguła prawej dłoni:

“Chwyć przewód prawą ręką

⇒ kciuk skierowany zgodnie z kierunkiem prądu i ⇒ palce zaciśnięte wokół przewodu skierowane są w kierunku linii pola magnetycznego”.

Ilustracja: opiłki żelaza na płycie kartonowej układają się w koncentryczne okręgi dzięki polu B wytworzonym przez prąd płynący w przewodzie.

Rów. (4) jest prawem `odwrotności kwadratu':

eksponent w mianowniku wynosi 3 tylko dlatego, iż w liczniku znajduje się
.

Kierunek i siłę pola magnetycznego B można opisać liniami pola [zielone kręgi] i wektorami pola [strzałki].

Linie pola B wytworzone przez prąd i płynący w długim prostym przewodzie tworzą koncentryczne okręgi dookoła przewodu; prąd skierowany ⊥ `do' kartki (symbol: ×).

Wektory pola są zawsze (w każdym punkcie linii) styczne do linii pola.

Kierunek
jest wynikiem iloczynu wektorowego
⇒ rozkład wektora
:

dB_|| (wzdłuż osi pętli);
( ⊥ do osi pętli)

Linie pola magnetycznego układają się wokół przewodu w kierunku przeciwnym do ruchu wskazówek zegara - przyjmując kierunek prądu jako `wychodzący' z kartki.

Śledzimy linie sił pola magnetycznego:

≡ ∑ po okręgu,

lecz B jest stałe w każdym miejscu na okręgu. Biorąc iloczyn skalarny:

Indukcja (B) • odległość = B(2πr) = μ_oi.

Jest to proste zastosowanie prawa Ampera.

B_a (zielona strzałka) - pole od przewodu `a' w miejscu gdzie znajduje się przewód `b'.

B_a działa na prąd i_b dając siłę F_ba (niebieska strzałka) na odcinku L przewodu `b'.

F_ba = siła działająca na przewód `b' pochodząca od prądu i<sub>a</sub> w przewodzie `a'.

Rów. (2) nadal jest prawem `odwrotności kwadratu':
zależy od odwrotności r² ; wielkość (
/r) jest wersorem w kierunku
.

SOLENOID

[Rys. lewy = L; prawy = P]

Rys. 1a: Składowa ładunku dq wytwarza różniczkowe pole elektryczne
w punkcie P.

Dla toroidu, prawo Ampera (z pokazaną pętlą amperowską) dostarcza wyrażenia na wewnętrzne pole magnetyczne (tj. wewnątrz rurki w kształcie obważanka) jako:

(B)(2πr) = μ_oiN

⇒

N - całkowita liczba zwojów;

r - odległość od środka toroidu do punktu wewnątrz toroidu

Prawo Ampera pokazuje, że:

U1: B nie jest stałe poprzez przekrój toroidu (inaczej niż dla solenoidu).

U2: B = 0 dla punktów na zewnątrz idealnego toroidu (tak jakby toroid został zrobiony z idealnego solenoidu).

Prawo Ampera: Wartość całki okrężnej wektora natężenia pola magnetycznego, wytworzonego przez stały prąd elektryczny w przewodniku wzdłuż linii zamkniętej otaczającej prąd, jest równa sumie algebraicznej natężeń prądów przepływających (strumieniowi gęstości prądu) przez dowolną powierzchnię objętą przez tę linię. (Wikipedia)

Zastosowanie = działo szynowe:

Dwie metalowe szyny włączenie prądu powoduje stopienie bezpiecznika (cienki kawałek miedzi) wytwarza się przewodzący gaz, który jako część obwodu prądowego podlega sile z pola B siła jest skierowana na zewnątrz, równolegle do szyn gaz przesuwa się wzdłuż szyn wypychając pocisk.

Pocisk może uzyskać w krótkim czasie bardzo duże przyśpieszenie i prędkość.

U1: Jedna strona pętli działa jak biegun północny (w kierunku μ) a druga jako biegun południowy, tak jak sugeruje magnes, delikatnie naniesiony na rysunek.

U2: Moment magnetyczny pętli z prądem jest równoważny momentowi magnetycznemu magnesu sztabkowego.

U3: Kołowa pętla (≡ ZWÓJ)

jest równoważny magnesowi sztabkowemu (≡ dipol magnetyczny).

Wielkość pola magnetycznego B pochodzącego od nieskończenie długiego przewodu z prądem i, w punkcie P - w odległości prostopadłej (⊥) do przewodu:

⇒
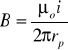
(5) [Dowód tego wzoru - HRW]

U1: W rów. (5): r_p = ⊥ odległość, to nie jest wektor tak jak w prawie Biota-Savarta!

1. φ - kąt w radianach

⇒ ds = Rdφ

2. kąt pomiędzy
i
wynosi 90^o

⇒ w Rów. (3): θ = 90^o, r = R

3. w środku C pole B wytworzone

przez prąd i w przewodzie jest w

kierunku `wychodzącym'

z kartki.

Składowe
pochodzące od wszystkich części pętli (A - prawa i A′ - lewa) niwelują się nawzajem:
⇒ całkowite

(A)

(A′)

⇒ Całkowite pole magnetyczne musi być skierowane tylko w kierunku dB_||.

⇒
⇒

Zakładamy: długość solenoidu l >> średnicy 2r

Te własności kołowej pętli z prądem można odnieść do pojedynczego elektronu krążącego po orbicie wokół jądra w atomie [= model Bohra]

Kwantowe pochodzenie momentów magnetycznych

Równoległe prądy przyciągają się,

a antyrównoległe odpychają się.

Lewa strona równania (LSR) =

Prawa strona równania (PSR)

---