Poznań dnia 25.09.2001r.

Laboratorium fizyki
Ćwiczenie nr O3 Wyznaczanie współczynnika załamania światła za pomocą refraktometru Abbego
ZSI-28	Pluton 3	Zamelczyk Jarosław Kopka Krzysztof
25.09.2001r.	Ocena:

1. Wstęp teoretyczny:

Współczynnik załamania światła i wszystkie z nim związane wartości opisuje tzw prawo załamania Snelliusa które można przedstawić w następującej postaci jeżeli monochromatyczna fala świetlna pada na gładką powierzchnię rozdzielającą dwa przezroczyste ośrodki:

α

ośrodek I

ośrodek II

β

=

gdzie nI i nII to są współczynniki załamania w ośrodkach.

Powyższe możemy przedstawić z wartościami prędkości rozchodzenia się światła vI i vII

I wówczas wzór przyjmuje postać:

=

Jeżeli pierwszym ośrodkiem jest powietrze, to możemy przyjąć że nI=1 i prawo to ma postać:

= nII

Na rysunku przedstawiona jest fala świetlna rozchodząca się w ośrodku optycznie rzadszym padająca na granicę z ośrodkiem gęstszym i załamująca się w kierunku normalnej gdzie kąt padania jest większy od kąta załamania. Analizując sytuację odwrotną gdzie kąt załamania jest większy od kąta padania możemy zwiększyć kąt padania do stanu gdy kąt załamania będzie równy π/2. Odpowiadający mu kąt padania nazywamy kątem granicznym gdyż dla każdego kąta padania większego od kata granicznego nastąpi całkowite odbicie wewnątrz ośrodka optycznie gęstszego. Na podstawie prawa Snelliusa kąt graniczny określony jest następującymi wzorami:

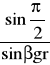
= n

= n
sin
gr =

czyli βgr = arc sin

Pomiar kata granicznego może być wykorzystany do wyznaczania współczynnika załamania światła. Na powyższej zasadzie oparta jest budowa refraktometru Abbego.

Aby wyznaczyć współczynnik załamania światła danego ośrodka potrzebny jest uniwersalny refraktometr Abbego. Używanie zwykłego refraktometru wymaga stosowania typowego światła monochromatycznego, gdyż przy stosowaniu światła białego występuje zjawisko dyspersji i linia graniczna dwóch ośrodków jest nieostra.

2. Cel do osiągnięcia:

Celem ćwiczenia jest wyznaczenie współczynnika załamania światła dla różnych cieczy, a następnie wyliczenie ich kątów granicznych.

Dla jednej z cieczy należy zbadać zależność współczynnika załamania światła od temperatury i na podstawie pomiarów wykonać wykres, gdzie będzie widoczna linia trendu.

Wyniki pomiarów oraz błąd odczytu współczynnika załamania światła Δn i błąd pomiaru temperatury Δt należy zapisać w tabelach.

3. Wyniki pomiarów:

		Współczynnik załamania światła
Substancja		1	2	3	4	5	Średnia	Błąd odczytu
1	Olej nr1	1,489	1,489	1,488	1,489	1,488	1,488	0,001
2	Olej nr 2	1,556	1,556	1,557	1,556	1,556	1,556	0,001
3	Denaturat	1,365	1,365	1,364	1,365	1,365	1,365	0,001
4	Woda	1,333	1,333	1,334	1,334	1,333	1,333	0,001

4. Wyznaczenie kąta granicznego badanych próbek

Kąt graniczny wyznaczmy ze wzoru :

βgr = arc sin 1/n

olej nr 1 = 39,96º

olej nr 2 = 47,09º

denaturat = 44,37º

woda = 48,57º

5. Zestawienie tabelaryczne powyższych zależności:

Numer próbki	Współczynnik załamania światła (średnia z 5 pomiarów)	Kąt graniczny β
Olej nr 1	1,488	39,96°
Olej nr 3	1,556	44,37°
Denaturat	1,365	47,09°
Woda	1,333	48,57°

7. Wnioski:

Wyznaczanie współczynnika załamania za pomocą uniwersalnego refraktometru Abbego jest szybką i prostą metodą dowiedzenia poprawności prawa Snelliusa. Dodatkowe urządzenia kompensujące dyspersje optyczną pozwalają na dokładne odczyty mimo użycia światła białego. Na poprawność dokładnych odczytów ma duży wpływ czystość pryzmatów, dlatego po każdym pomiarze należy starannie je wyczyścić i osuszyć przed rozprowadzeniem badanej cieczy. Jedynym poważnym mankamentem przy odczycie może być tylko zły wzrok obsługującego, który źle odczyta skalę podziałki.

---