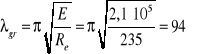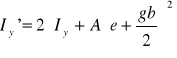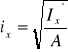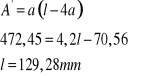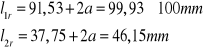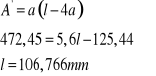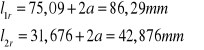Spis treści:
I. Schemat kratownicy 3
II. Mechanika obciążeń:
2-1 Siły czynne w kratownicy 4
2-2 Sprawdzenie warunku statycznej wyznaczalności kratownicy 4
2-3 Wyznaczenie sił biernych (reakcji) 4
2-4 Wyznaczenie sił w prętach 5
2-5 Zestawienie wyników mechaniki obciążeń 8
III. Obliczenia wytrzymałościowe:
3-1 Dobranie prętów i blachy węzłowej kratownicy dla węzła 6 9
3-2 Obliczenia dla pręta ściskanego największą siłą ściskającą 10
IV. Projekt węzła nr 6:
4-1 Obliczenia wytrzymałościowe spoin 13
4-2 Rysunek złożeniowy węzła 1 załącznik
4-3 Rysunek węzła w izometrii załącznik
2
1.Schemat kratownicy
3
Dane |
Obliczenia |
Wyniki |
2 |
Mechanika obciążeń
|
|
2-1
P = 25 [kN] = 25000 [N]
a = 1000 [mm] |
Siły czynne
|
|
2-2 |
Sprawdzenie warunku wyznaczalności statycznej kratownicy
Korzystamy z równania:
p = 2 . w - 3 , gdzie:
p = 11 - liczba prętów w = 7 - liczba węzłów
11 = 2 . 7 - 3
11 = 11 OK
Ustrój jest statycznie wyznaczalny.
|
|
2-3
|
Wyznaczenie sił biernych (reakcji)
Korzystamy z warunku równowagi momentów względem punktów podparcia tj:
∑ MA = 0
∑ MB = 0
|
|
|
∑ MA = - P*a - 2*P*a + 3 RB*a = 0
RB = 3*P*a / 3*a = P = 25 [kN]
∑ MB = - 3*RA*a + 2*P*a + P*a = 0
RA = 3*P*a / 3*a = P = 25 [kN]
Sprawdzenie obliczeń:
|
RA = 25 [kN]
RB = 25 [kN] |
2-4 |
Wyznaczenie sił w prętach
WĘZEŁ 1
∑ Piy = 0 => RA - S15 . sin 600 = 0 S15 = RA / sin 600 = 28,867 [kN]
∑ Pix = 0 => S12 + S15 . cos 600 = 0 S12 = -S15 . cos 600 = - 14,443 [kN]
WĘZEŁ 5
∑ Piy = 0 => S15 . cos 300 + S25 . cos 300 = 0 S25 = - S15 = - 28,867 [kN]
|
S15 = 28,867 [kN] S12 = - 14,433 [kN] |
|
∑ Pix = 0 => -S15 . cos 600 + S25 . cos 600 + S56 = 0 S56 = -S25 . cos 600 + S15 . cos 600 = 28,867 [kN]
WĘZEŁ 2
∑ Piy = 0 => -P - S25 . sin 600 - S26 . sin 600 = 0 S26 = (-P - S25 . sin 600 ) / sin 600 = 0 [kN]
∑ Pix = 0 => - S12 - S25 . cos 600 + S23 + S26 . cos 600 = 0 S23 = S12 + S25 . cos 600 - S26 . cos 600 = - 28,867 [kN]
WĘZEŁ 6
∑ Piy = 0 => - S26 . sin 600 + S36 . sin 600 = 0 S36 = S26 = 0 [kN]
∑ Pix = 0 => - S56 - S26 . cos 600 + S36 . cos 600 + S67 = 0 S67 = S26 . cos 600 + S56 - S36 . cos 600 = 28,867 [kN] |
S25 = - 28,867 [kN] S56 = 28,867 [kN]
S26 = 0 [kN] S23 = - 28,867 [kN]
S36 = 0 [kN] S67 = 28,867[kN] |
|
WĘZEŁ 3
∑ Piy = 0 => - P - S36 . sin 600 - S37 . sin 600 = 0 S37 = ( - P - S36 . sin 600 ) / sin 600 = - 28,867 [kN]
∑ Pix = 0 => -S23 - S36 . cos 600 + S34 + S37 . cos 600 = 0 S34 = S23 + S36 . cos 600 - S37 . cos 600 = - 14,433 [kN]
WĘZEŁ 7
∑ Piy = 0 => S37 . sin 600 + S47 . cos 300 = 0 S47 = ( - S37 . sin 600 ) / cos 300 = 28,867 [kN]
∑ Pix = 0 => - S67 - S37 . cos 600 + S47 . sin 300 = 0 S67 = S47 . sin 300 - S37 . cos 600 = 28,867 [kN] |
S37 = - 28,867[kN] S34 = -14,433 [kN]
S47 = 28,867 [kN] |
2-5 |
Zestawienie wyników mechaniki obciążeń
Siły rozciągające pręty:
Siły ściskające pręty:
Siły zerowe:
|
|
Schemat prętowy kratownicy z zaznaczonymi prawidłowymi zwrotami sił wewnętrznych w prętach .
3 |
Obliczenia wytrzymałościowe |
|
||||
3-1
Re = 235 MPa |
Dobranie prętów i blachy węzłowej kratownicy dla węzła 6
Analiza węzła 6:
Pręt 6(S56) i pręt 5(S67) są rozciągane i ich wymiary należy dobrać z warunku na rozciąganie. Siły działające na pręt 9(S26) i pręt 10(S36) są równe zero , mimo tego dobiorę pręty , identyczne jak w przypadku prętów 5 i 6.
Wszystkie elementy kratownicy wykonane zostaną ze stali S235. Dopuszczalne naprężenia na rozciąganie wynoszą:
kr = Re / xe
dla xe = 2 => kr = 235 MPa / 2 = 117,5 Mpa
Obliczenia wykonamy dla maksymalnej siły występującej w pojedynczym pręcie w węźle 6 tj:
S67= 28,867 [kN]
Obliczamy minimalny przekrój pręta:
σ = S67/A < kr => A > S67 / kr
A > 28867 [N] / 117,5 MPa > 246 [mm2]
Ponieważ pręty wykonywane będą z dwóch symetrycznych kątowników równoramiennych, pole pojedynczego kątownika musi być większe od 123 [mm2]
Na podstawie PN-84/H-93401 dobieramy kątownik równoramienny 25x25x3 o polu przekroju poprzecznego wynoszącym 142 mm2 i momencie bezwładności Ix = Iy = 0,79 cm4 i e =0,73 cm.
|
S26 = 0 [kN] S36 = 0 [kN] S67 = 28,867[kN] S56 = 28,867 [kN]
S67 = S56 S36 = S26
kr = 117,5 MPa
└ 25x25x3 |
||||
|
Na podstawie dobranego profilu ustalamy grubość blachy węzłowej - korzystamy ze wzoru:
gbw = 1,6*gmin , gdzie: gmin - minimalna grubość profilu = 3 mm,
gbw = 1,6*3 mm = 4,8 mm
Dobieramy blachę węzłową o grubości 6 mm. |
gbw = 6 [mm] |
||||
3-2 |
Obliczenia dla pręta ściskanego z warunku na wyboczenie dla największej siły ściskającej w kratownicy
Pręt ten ponieważ jest ściskany należy dobierać ze względu na wyboczenie (kątownik równoramienny spawany obustronnie) Wstępny dobór kształtownika z warunku na ściskanie.
Przyjmuje naprężenia ściskające
Na podstawie PN-84/H-93401 dobieramy kątownik równoramienny 30x30x4 o polu przekroju poprzecznego wynoszącym 227 mm2 i momencie bezwładności Ix = Iy = 1,81 cm4 i e =0,89 cm.
Dobieram kątownik 30x30x4
Obliczam moment bezwładności dla połączonego kątownika i blachy węzłowej, przyjmując jej grubość : gb=1,6 g Ix'= Ix Na podstawie dobranego profilu ustalamy grubość blachy węzłowej - korzystamy ze wzoru:
gbw = 1,6*gmin , gdzie: gmin - minimalna grubość profilu = 4 mm,
gbw = 1,6*4 mm = 6,4 mm
Dobieramy blachę węzłową o grubości 8 mm.
Ponieważ pręty są mocowane w dwóch przegubach, współczynnik zamocowania α = 1.
Zatem długość zredukowana lr = α . l = 1000 mm.
Dla stali S235 przyjmujemy
λgr = 94 Mpa
Ponieważ Ix'< Iy' - pręt jest bardziej narażony na wyboczenie względem osi ox.
Obliczamy minimalny promień bezwładności:
Obliczam smukłość pręta:
λ > λgr => wyboczenie sprężyste
σkr = (π2 . E) / λkr2 = 234,56 Mpa
Korzystamy z warunku bezpieczeństwa na wyboczenie:
P / A < σkr / nw , gdzie:
nw - współczynnik bezpieczeństwa, równy przy obciążeniach statycznych 3,5
Warunek na wyboczenie jest spełniony, zatem pręt nie ulegnie wyboczeniu.
|
S25 = -28,867[kN]
└ 30x30x4 gbw = 8 [mm] |
||||
4 |
Projekt węzła nr 6
|
|
||||
4.1 |
Obliczenia długości spoin
Blachę węzłową łączymy z prętami za pomocą spoin pachwinowych.
Grubość tych spoin wyliczamy ze wzoru: a = 0,7*g , gdzie g - minimalna grubość łączonych elementów
a = 0,7*6 = 4.2 mm
PRĘT 6 (S56)
Obliczamy naprężenia dopuszczalne w spoinie korzystając z zależności:
kt' = z0 . z . kr , gdzie:
z - współczynnik jakości spoiny równy 0,8 z0 - współczynnik wytrzymałości spoiny równy 0,65
kt' = 0,8*0,65*117,5 MPa = 61,1 Mpa
Obliczanie długości spoiny dla pręta 6
Uwzględniając kratery na końcach spoin rzeczywiste długości wynoszą:
Obliczenia długości spoin dla pręta ściskanego S25 = -28,867[kN]
Blachę węzłową łączymy z prętami za pomocą spoin pachwinowych.
Grubość tych spoin wyliczamy ze wzoru: a = 0,7*g , gdzie g - minimalna grubość łączonych elementów
a = 0,7*8 = 5,6 mm
PRĘT 8 (S25)
Obliczamy naprężenia dopuszczalne w spoinie korzystając z zależności:
kt' = z0 . z . kr , gdzie:
z - współczynnik jakości spoiny równy 0,8 z0 - współczynnik wytrzymałości spoiny równy 0,65
kt' = 0,8*0,65*117,5 MPa = 61,1 Mpa
Obliczanie długości spoiny dla pręta 8
Uwzględniając kratery na końcach spoin rzeczywiste długości wynoszą:
|
|
||||
Wyszukiwarka
Podobne podstrony:
Pytania z Kolosa z PKMu, PKM egzamin kolosy ( łukasik, Salwiński )
projekt 5a, PKM egzamin kolosy ( łukasik, Salwiński )
PRZEK+üADNIA Z BATA, PKM egzamin kolosy ( łukasik, Salwiński )
zestaw 4, PKM egzamin kolosy ( łukasik, Salwiński )
WIBROA-00-01, PKM egzamin kolosy ( łukasik, Salwiński )
PKM sciaga 1, PKM egzamin kolosy ( łukasik, Salwiński )
4 mini, PKM egzamin kolosy ( łukasik, Salwiński )
SCIAGA pkm polaczenia nierozlaczne, PKM egzamin kolosy ( łukasik, Salwiński )
PYTANIA Z ZERóWKI, PKM egzamin kolosy ( łukasik, Salwiński )
sciaga 5, PKM egzamin kolosy ( łukasik, Salwiński )
4(2), PKM egzamin kolosy ( łukasik, Salwiński )
PKM I ściąga, PKM egzamin kolosy ( łukasik, Salwiński )
Spr yny, PKM egzamin kolosy ( łukasik, Salwiński )
Przek adnia limakowa, PKM egzamin kolosy ( łukasik, Salwiński )
a, PKM egzamin kolosy ( łukasik, Salwiński )
teczka, PKM egzamin kolosy ( łukasik, Salwiński )
kolos z przekladni, PKM egzamin kolosy ( łukasik, Salwiński )
więcej podobnych podstron