Zadania do samodzielnego rozwiązania przed egzaminem
Obliczyć

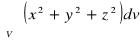
, gdzie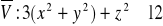
.Obliczyć objętość bryły zawartej wewnątrz walca o równaniu

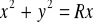
i sfery o równaniu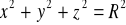
.Korzystając z całki krzywoliniowej skierowanej obliczyć pole ograniczone pętlą Kartezjusza :
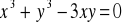
, (wsk. y=xt, 0
t
1).Obliczyć pole powierzchni walca S : y2+z2=r2, ograniczonej walcem o równaniu
x2+y2=r2.
Obliczyć strumień wektora pola
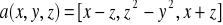
przez zorientowaną
zewnętrznie powierzchnię całkowitą walca x2+y2=4 dla z![]()
<0;4>.
Sprawdzić tezę twierdzenia Stokesa-Ampera dla pola wektorowego
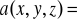
=[x,x+y,x+y+z] i krzywej L o przedstawieniu parametrycznym : x=2cost, y=2sint,
z=2(cost+sint), dla t![]()
<0;2![]()
>.
Sprawdzić tezę twierdzenia Stokesa-Ampera dla pola wektorowego
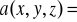
=[2x,xy2,3xyz] i krzywej L będącej brzegiem gładkiego płata powierzchniowego
S : z=2-x2-y2 dla x2+y2![]()
8. Wyznaczyć punkty, w których funkcja f(z)=z![]()
2 ma pochodną i obliczyć jej pochodną w
tych punktach.
9. Znaleźć funkcję holomorficzną f(z)=u(x,y)+jv(x,y) spełniającą warunek f(0)=0, jeżeli
u(x,y)=cosxshy, b) v(x,y)=ex(xcosy-ysiny).
10. Obliczyć całkę ![]()
, gdzie K jest dodatnio skierowanym względem wnętrza
okręgiem o równaniu ![]()
=1.
Rozwinąć w szereg Taylora w otoczeniu punktu z0=-3 funkcję

f(z)=z2ez i podać
promień zbieżności tego szeregu.
Rozwinąć w szereg Laurenta funkcję f(z)=
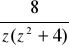
w pierścieniu
P(0;0,2), b) P(2j;0,2), c) P(-2j;2,4) .
Korzystając z twierdzenia o residuach obliczyć całkę
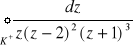
, K: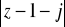
=2,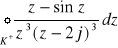
, K: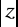
=1.
Obliczyć L-transformatę oryginału f(t)1(t), gdzie
f(t)=cos2
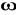
t, b) f(t)=sin2tcos3t, c) f(t)=t2e-3tsin2t.
Obliczyć L-1-transformatę funkcji
a) ![]()
(s)=![]()
, b) ![]()
(s)=![]()
, c) ![]()
(s)=![]()
.
Obliczyć splot f1(t)
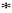
f2(t) oryginałów
f1(t)=e3t , f2(t)=e5t ; b) f1(t)=et , f2(t)=t2 ; c) f1(t)=f2(t)=sint.
Znaleźć CS równania różniczkowego przy podanych warunkach początkowych
x(4) +x=2et , x(0)=x"(0)=0 , x'(0)=x(3)(0)=1,
x(3)-x'=-2t , x(i)(0)=i dla i=0,1,2 .
Znaleźć CS układu równań różniczkowych przy podanych war.początkowych
x'-2y'+x=1, y'+x-2y=e-t, x(0)=1 i y(0)=0,
x'+x-y-z=et, y'-x+y-z=e3t, z'-x-y-z=4, x(0)=-
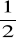
, y(0)=-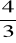
, z(0)=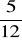
.
Pole wektorowe
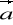
=[P,Q,R] i pole skalarne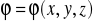
są klasy C2. Wykazać, że
div(rot
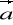
)=0, b) rot(grad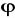
)=0, c) rot(rot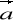
)=grad(div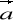
)-
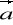
.
Wykazać, że jeżeli pola wektorowe
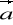
=[P1,Q1,R1] i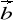
=[P2,Q2,R2] są klasy C1, to
div(![]()
![]()
)=![]()
![]()
-![]()
![]()
.
Pole wektorowe
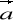
=[P,Q,R] i pole skalarne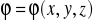
są klasy C1. Wykazać, że
rot(
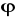
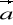
)=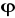
rot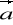
+(grad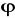
)
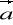
,div(
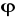
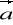
)=(grad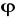
).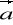
+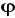
div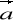
.
Wykazać, że jeżeli
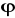
(x,y,z) jest klasy C2, to
div(grad
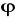
)=
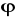
, b)
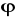
=∇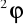
.
Wykazać, że jeżeli
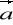
=[P,Q,R] jest polem wektorowym klasy C3, to
div(∇2![]()
)=∇2(div![]()
).
Odpowiedzi (wzkazówki)
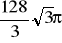
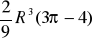
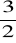
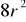
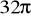
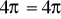
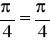
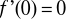
a)
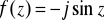
b) ![]()
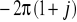
Wsk.
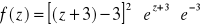
Wsk.
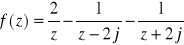
a)
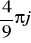
, b) 0a)
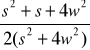
b) 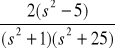
c) 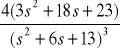
a)
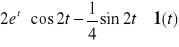
b) ![]()
c) ![]()
a)
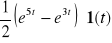
b) ![]()
c) ![]()
a)
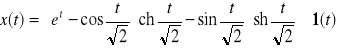
b) ![]()
a)
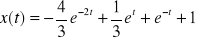
,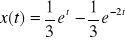
b) 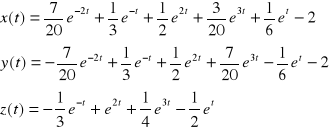
Wyszukiwarka
Podobne podstrony:
zadania dodatkowe, Ekonomia- studia, Finanse publiczne i rynki finansowe
Sciaga(1), Księgozbiór, Studia, Matematyka
mata egz, Księgozbiór, Studia, Matematyka
zadania dodatkowe, Ekonomia- studia, Finanse publiczne i rynki finansowe
Zadania dodatkowe z AM (5), Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matemat
Planimetria i geometria analityczna zadania, Zadania na studia z matematyki
Zadania dodatkowe, studia wsiz, semestr 1 2, programowanie LAB wyklad, Programowanie, BFryc, 1IID, Z
zadania na szóstkę kl 4, PRACA, matematyka, kl. 4, zadania dodatkowe
Zadania na egzamin ;-), Studiaa xD, matma, Matematyka, Matematyka
Zadania Temat1 Procent prosty, STUDIA, Matematyka finansowa
Figury na płaszczyźnie - zadania, Zadania na studia z matematyki
Równania różniczkowe sciąga, Politechnika Lubelska, Studia, Studia, Sprawozdania, studia, Matematyka
Zadania z matematyki z 30, Politechnika Lubelska, Studia, Studia, Sprawozdania, studia, Matematyka,
Elektryka - Zadania, Księgozbiór, Studia, Elektronika i Elektrotechnika
Matematyka dyskretna zadania dodatkowe
Przebieg rozumowania zadania metodą syntetyczną, Studia UJK, Matematyka
Zadania dodatkowe z matematyki dla klas VI w m, klasa 6
matma zadania, Budownictwo-studia, Matematyka
więcej podobnych podstron