Prawa Keplera.

Na podstawie zebranych obserwacji astronomicznych Kepler sformułował trzy podstawowe prawa ruchu planet:

I - Orbita każdej planety jest elipsą, przy czym Słońce znajduje się zawsze w jednym z ognisk elipsy.

II - Prędkość polowa każdej planety jest stała, co oznacza, że wektor położenia planet zakreśla w jednakowych przedziałach czasu równe pola. Zgodnie z drugim prawem Keplera okres T obrotu planety wokół słońca jest równy stosunkowi pola powierzchni S orbity do prędkości polowej tej planety
tej planety:
, gdzie
i
są odpowiednio dużą i małą osią orbity eliptycznej.

III - Stosunek kwadratu okresu T obiegu planety dookoła Słońca do sześcianu średniej odległości R od niego jest dla wszystkich planet Układu Słonecznego jednakowy:
.

Jeżeli w przybliżeniu ruch każdej planety będzie uważany za ruch punktu materialnego w centralnym polu grawitacyjnym, wówczas prawa Keplera są prostą konsekwencją zasad dynamiki i prawa powszechnego ciążenia.

Prawo powszechnego ciążenia; stała grawitacji.

Na ciało umieszczone w skończonej odległości od innego ciała działa siła grawitacji( siła ciężkości), a wytworzone przez to ciało pole nazywamy polem grawitacyjnym lub polem ciężkości. Podstawową właściwością pola grawitacyjnego jest to, że na każdy punkt materialny umieszczony w tym polu działa siła zwrócona w stronę pewnego punktu zwanego środkiem ciężkości źródła pola. Wartość siły grawitacji określa prawo powszechnej grawitacji (powszechnego ciążenia) wyrażone wzorem:
gdzie:
-stała grawitacji,
- siła działająca na punkt 1 ze strony punktu 2,
- wektor poprowadzony z punktu 2 do punktu 1; wektor
ma wartość równą 1 i wyznacza kierunek w przestrzeni od punktu 2 do punktu 1.

Ciało o masie
jest przyciągane przez ciało o masie
z siłą o zwrocie przeciwnym do wektora położenia łączącego ciało 1 z ciałem 2. Prawo powszechnego ciążenia Izaaka Newtona orzeka: między każdymi dwoma punktami materialnymi działają siły przyciągania wzajemnego, które są wprost proporcjonalne do mas tych punktów i odwrotnie proporcjonalne do kwadratu odległości między nimi. Współczynnik proporcjonalności zastosowany w tym równaniu nosi nazwę stałej grawitacji. Stała grawitacji jest liczbowo równa sile wzajemnego przyciągania dwóch punktów materialnych o jednostkowych masach oddalonych od siebie o jednostkę długości. Doświadczalnie wyznaczona wartość G jest równa
.

Pojęcie pola fizycznego. Pole grawitacyjne. Natężenie pola grawitacyjnego;

linie pola. Pole centralne i jednorodne.

Polem fizycznym, lub po prostu polem, nazywamy szczególną formę materii, wiążącą cząstki substancji w układy, a także przekazującą ze skończoną prędkością oddziaływanie jednych cząstek na drugie. Wzajemne oddziaływanie między oddalonymi od siebie ciałami następuje za pomocą wytwarzanych przez nie pól grawitacyjnych bądź elektromagnetycznych( np. przyciąganie planet przez Słońce, wzajemne oddziaływanie ciał obdarzonych ładunkiem elektrycznym, przewodników z prądem). Mechaniczne oddziaływanie na dane ciało ze strony innych ciał może przejawiać się dwojako. Może ono spowodować: po pierwsze, zmianę stanu ruchu mechanicznego rozpatrywanego ciała i po drugie, jego odkształcenie. W uproszczony sposób można powiedzieć, że pole fizyczne, jest przestrzennym rozkładem wielkości fizycznych np. pole temperatury, pole ciśnienia, pole siły. Oddziaływania grawitacyjne między ciałami następują za pośrednictwem wytwarzanych przez nie pól grawitacyjnych nazywanych także polami ciężkości. Wyróżniająca pole grawitacyjne własność polega na tym, że na umieszczony w nim punkt materialny działa siła proporcjonalna do masy tej cząstki. Wielkością charakteryzującą pole grawitacyjne jest jego natężenie - wielkość wektorowa
(gama), równa stosunkowi siły
, jaką pole wywiera na umieszczony w nim punkt materialny do masy tego punktu
:
(def.). Natężenie pola grawitacyjnego nie zależy od masy
punktu materialnego. (
- siła ciążenia - prawo rządzące oddziaływaniem pola grawitacyjnego na ciało o masie m umieszczone w danym miejscu pola, o natężeniu
). Wzór na wartość natężenia centralnego pola grawitacyjnego:
- wartość natężenia pola grawitacyjnego jest wprost proporcjonalna do masy M źródła pola, a odwrotnie proporcjonalna do kwadratu odległości r punktu, w którym je mierzymy, od źródła pola.

Linie natężenia sił pola są to proste lub krzywe, do których wektor natężenia pola jest styczny w każdym punkcie pola. Liniom pola przypisujemy zwrot zgodny do ze zwrotem natężenia pola. Pole jednorodne jest polem, którego linie pola są do siebie równoległe, a natężenie pola ma w każdym jego punkcie tę samą wartość. W przypadku pola grawitacyjnego, niewielki fragment centralnego pola grawitacyjnego możemy traktować jako jednorodne pole grawitacyjne. Pole centralne - pole wykazujące przestrzenna symetrię, pole daleko Ziemi.

Natężenie pola grawitacyjnego a przyśpieszenie ziemskie.

Jeżeli w polu grawitacyjnym o natężeniu
umieścimy punkt materialny, to po wpływem siły grawitacji poruszać się on będzie z przyśpieszeniem grawitacyjnym, które możemy obliczyć stosując II zasadę dynamiki:
. Jak widać, przyśpieszenie grawitacyjne
zdefiniowane jako stosunek siły działającej na ciało do jego masy, przypomina definicję natężenia pola grawitacyjnego. Wobec tego możemy zapisać:
. Przyśpieszenie grawitacyjne charakteryzuje ruch określonego punktu materialnego, a natężenie pola grawitacyjnego charakteryzuje właściwości pola grawitacyjnego, niezależnie od tego, czy znajduje się w nim jakiekolwiek ciało. Są to, zatem dwie różne wielkości fizyczne. Ze względu na to, że
nie zależy od masy ciała poruszającego się w polu grawitacyjnym, najrozmaitsze ciała muszą spadać w danym punkcie pola grawitacyjnego Ziemi z jednakowym przyśpieszeniem, jeśli jedyną siłą działającą na każde z nich jest siła grawitacji. (
- sytuacja taka ma miejsce na biegunach, bo:
, gdzie
- ciężar ciała,
siła ciążenia,
- odśrodkowa siła bezwładności;
- prędkość kątowa Ziemi,
- odległość ciała od osi obrotu Ziemi:
,
- szerokość geograficzna miejsca, w którym znajduje się ciało,
- promień ziemi.
wtedy gdy szerokość geograficzna wynosi
i dlatego
a co za tym idzie
).

Praca w polu grawitacyjnym; zachowawczy charakter pola grawitacyjnego.

Definicja na pracę
jest słuszna wówczas, gdy pracę wykonuje stała siła
, tj. mająca w każdym punkcie przemieszczenia
taką samą wartość, kierunek i zwrot. W naszym przypadku:
, gdzie
. Ale
nie jest siłą stałą, ponieważ:
,
. W celu dalszych obliczeń należy wprowadzić siłę średnią, będącą geometryczna średnią obu tych sił:
, czyli: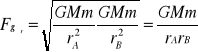
. Siła grawitacji z wektorem przemieszczenia ciała tworzy kąt 180°( cos180°= - 1) więc:
,
,
jest to praca wykonywana przez siłę grawitacji
.
, ponieważ
(
,
,
,
)

Pole grawitacyjne jest polem zachowawczym(konserwatywnym), ponieważ:

Praca sił pola grawitacyjnego nie zależy od kształtu toru, po którym ciało jest przemieszczane w polu, lub: praca wykonywana przez siły pola podczas przemieszczania ciała po torze zamkniętym jest równa 0. Wynika to ze wzoru na pracę w polu grawitacyjnym:
.

Energia potencjalna ciała w polu grawitacyjnym; sens fizyczny przyrostu energii

potencjalnej. Zasada zachowania energii mechanicznej.

Kosztem pracy wykonanej przez siły zewnętrzne, przeciw siłom pola grawitacyjnego podczas przemieszczenia ciała z punktu A pola do punktu B pola, ruchem jednostajnym, ulegnie zmianie energia ciała, którą nazywamy energią potencjalną (ciężkości) grawitacji. Energią potencjalną nazywamy część energii mechanicznej( energia mechaniczna - energia układu związana z ruchem i oddziaływaniem poszczególnych części układu mechanicznego równa sumie energii kinetycznej i energii potencjalnej) układu zależną tylko od jego konfiguracji, czyli od wzajemnego rozmieszczenia wszystkich cząstek( punktów materialnych) układu i ich położenia w zewnętrznym polu sił. Przyrost energii potencjalnej układu jest równy pracy, którą muszą wykonać siły zewnętrzne działające na dany układ przy przeprowadzeniu układu od konfiguracji, dla której energie potencjalną umownie przyjmuje się za równą 0, w daną konfigurację.

Energia potencjalna jest równa pracy sił zewnętrznych przy przenoszeniu ciała z punktu A do nieskończoności:
bo 1/∞ = 0. Czyli
- dla pola jednorodnego,
- w polu jednorodnym.

Całkowitą energię mechaniczną układu izolowanego( układ ciał, na który nie działają siły zewnętrzne) nazywamy sumę energii kinetycznej ciał wchodzących w skład układu oraz energii potencjalnej. Jest to zatem wielkość skalarna. Energia potencjalna wynikająca z oddziaływania między dwoma ciałami jest równa energii potencjalnej jednego ciała w polu wytworzonym przez drugie ciało. Wartość energii potencjalnej oddziaływania nie zależy od tego, które z ciał uznamy za źródło siły, a które za obiekt działania siły. Z zasady dynamiki wynika: Dla układu izolowanego, w którym wszystkie siły są zachowawcze, całkowita energia mechaniczna jest wielkością stałą. Jest to prawo zachowania energii mechanicznej. Stanowi ono szczególny przypadek bardziej ogólnej zasady zachowania energii. Prawo zachowania energii mechanicznej spełniają tyko proste układy, w których wszystkie siły oddziaływania mają charakter grawitacyjny, elektrostatyczny lub są siłami sprężystymi. Energia kinetyczna i potencjalna jest zachowana tylko w przypadku działania sił zachowawczych.

Potencjał grawitacyjny; powierzchnie ekwipotencjalne. Związek między liniami

pola a powierzchniami ekwipotencjalnymi.

Właściwości energetyczne pola grawitacyjnego w danym punkcie pola pozwala określić wielkość zwana potencjałem grawitacyjnym V, gdzie
(def). Potencjałem pola grawitacyjnego nazywamy stosunek energii potencjalnej punktu materialnego, umieszczonego w danym punkcie pola, do jego masy; wzór na wartość potencjału centralnego pola grawitacyjnego:
, gdzie G - stała grawitacji; M - masa źródła; r - odległość od źródła. Potencjał jest wielkością skalarną. Zbiór punktów o tej samej wartości potencjału tworzy powierzchnię ekwipotencjalną. Cechy powierzchni ekwipotencjalnych: 1) praca sił równa się zeru na dowolnej drodze leżącej na takiej powierzchni; 2) w dowolnym punkcie pola siła ( natężenie) ma kierunek prostopadły do powierzchni ekwipotencjalnej przechodzącej przez ten punkt; 3) układ powierzchni ekwipotencjalnych przecina układ linii pola pod kątem prostym; 4) wektor natężenia pola jest skierowany od powierzchni o większym potencjale.

Prędkości kosmiczne. Loty kosmiczne: przeciążenie i nieważkość.

Pierwsza prędkość kosmiczna, to prędkość, jaką należy nadać (ciału) pojazdowi kosmicznemu, by mógł lotem bezsilnikowym okrążać Ziemią po orbicie kołowej. Rakieta nośna startuje z Ziemi, rozpędza się i osiąga prędkość styczną do orbity, po której ma poruszać się satelita. Osiągnąwszy potrzebną prędkość, rakieta odłącza się od satelity, pozostawiając go na orbicie.

Na poruszającego się po orbicie kołowej satelitę działa Ziemia siłą grawitacji:
, i w układzie nieinercjalnym siła odśrodkowa bezwładności( siła bezwładności występująca w układzie obracającym się. W ruchu jednostajnym ciała o masie m po okręgu o promieniu r wartość siły odśrodkowej bezwładności wynosi F = mω²r, gdzie ω - jest prędkością kątową obrotu układu odniesienia, w którym ciało spoczywa. Siła odśrodkowa skierowana jest wzdłuż promienia na zewnątrz.)
. Ponieważ obserwator znajduje się w układzie nieinercjalnym, te dwie siły równoważą się:
,
stąd
. Jak widać ze wzoru pierwsza prędkość kosmiczna jest wprost proporcjonalna do pierwiastka masy źródłowej, a odwrotnie proporcjonalna do pierwiastka promienia orbity i nie zależy od masy satelity. Podstawiając do wzoru masę Ziemi i promień Ziemi jako promień orbity( satelita krąży bardzo blisko powierzchni Ziemi), otrzymamy wartość pierwszej prędkości kosmicznej równą około 7,9km/s.

Druga prędkość kosmiczna to prędkość, jaką należy nadać pojazdowi kosmicznemu, by poruszając się dalej lotem bezsilnikowym, mógł opuścić dane pole grawitacyjne, a więc udać się do nieskończoności:

Przyjmijmy, że rakieta uzyskuje drugą prędkość kosmiczną tuż po starcie, więc blisko powierzchni masy źródłowej. Ma ona wtedy energię kinetyczną i potencjalną. Całkowita energia przy powierzchni masy źródłowej wynosi:
. Będąc w nieskończoności, rakieta ma energię równą zeru. Z prawa zachowania energii:
stąd
. Jak widać ze wzoru, druga prędkość kosmiczna jest wprost proporcjonalna do pierwiastka masy źródłowej, odwrotnie proporcjonalna do pierwiastka promienia masy źródłowej i nie zależy od masy statku kosmicznego. Porównując wartość pierwszej i drugiej prędkości kosmicznej otrzymamy:
. Dla ziemi
= 11,2 km/s.

Ciało spoczywające swobodnie na podłodze naciska na nią wskutek tego, że podłoga stoi na przeszkodzie jego spadaniu pod wpływem siły grawitacji. Podłoga równoważy siłę grawitacji przyłożoną do tego ciała. Gdyby jednak podłoga zaczęła z jakiegokolwiek powodu poruszać się ruchem przyśpieszonym w górę, musiałaby wywierać na dane ciało siłę większą niż jego ciężar, ponieważ musiałby mu nadać takie samo przyśpieszenie, z jakim się samo porusza. Ta dodatkowa siła określona jest drugą zasadą dynamiki: F = ma. Taką samą dodatkową siłą musi w tym czasie działać na podłogę dane ciało. Gdybyśmy trzymali to ciało w ręku, lub położyli je na wadze, stwierdzilibyśmy, że ciało stało się cięższe. Nie oznacza to wszakże, że zwiększyła się siła grawitacji, która zależy od wzajemnej odległości danego ciała i Ziemi - odległość ta prawie nie ulega zmianie. Przyczyną pojawienia się dodatkowego nacisku jest przyśpieszony ruch ciała pod wpływem przyłożonej siły. Jeżeli ciała wywierają na siebie wzajemny nacisk większy niż ten, jaki wywierają pod wpływem własnego ciężaru, mówimy, że są w stanie przeciążenia.

Jeśli stykające się ze sobą ciała spadają swobodnie( bez oporu), nie wywierają na siebie nacisku, ponieważ żadne z nich nie hamuje ani nie przyśpiesza ruchu drugiego ciała. Przedmioty znajdujące się wewnątrz pojazdu kosmicznego poruszającego się bez napędu po orbicie, poruszają się wszystkie z jednakowym przyśpieszeniem grawitacyjnym, które w tym ruchu jest przyśpieszeniem dośrodkowym. One również nie wywierają na siebie wzajemnego nacisku, mimo, że znajdują się pod wpływem pola grawitacyjnego, w którym się znajdują. Mówimy, że są one w stanie nieważkości. Brak wzajemnego nacisku ciał powodowanego siłą grawitacji określamy mianem stanu nieważkości. Podobnie, w stanie nieważkości pozostają ciała znajdujące się wewnątrz pojazdu kosmicznego lecącego bez napędu po jakimkolwiek torze. Wszystkie one poruszają się swobodnie razem z pojazdem nie napotykając żadnego oporu, żadne z nich nie hamuje ani nie przyśpiesza ruchu drugiego. Człowiek znajdujący się w takim pojeździe może odczuć nacisk innych ciał tylko wtedy, gdy zechce im nadać przyśpieszenie( np. chcąc je rzucić o ścianę) lub gdy uruchomi silnik swej rakiety. Wtedy podłoga lub fotel będzie nadawać mu przyśpieszenie, wywołując wzajemny nacisk. W tych warunkach wszystkie przedmioty w pojeździe staną się ważkie( ciężkie). Nie będzie to jednak wynikiem działania siły grawitacji, lecz siły bezwładności, przyciskającej dane ciało do tylnej ściany pojazdu. Jest bardzo ciekawe, że pasażer pojazdu kosmicznego nie może odróżnić sił bezwładności działających w pojeździe poruszającym się ruchem zmiennym( przy włączonych silnikach) od siły grawitacji, jeśli nie wie o tym, że silniki są włączone.

---